2.5. Разложение функций в степенной ряд Тейлора
Всякая
функция f(x),
бесконечно дифференцируемая в интервале
,
может быть разложена в этом интервале
в сходящийся к ней степенной ряд Тейлора
,
(15)
если
в этом интервале выполняется условие:
где
остаточный
член формулы Тейлора, записанный в форме
Лагранжа,
где
-
положительное число меньше 1.
При
ряд
Тейлора называют рядом Маклорена:
.
(15)
Если
в некотором интервале, содержащем точку
,
все производные
ограничены некоторой константой, т.е.
при любом n
выполняется неравенство
,
где М – положительная постоянная, то
.
Тогда функция f(x)
будет суммой ряда (15), причем только для
тех значений х, при которых
при
(необходимое
и достаточное условие равенства (15) в
разложении f(x)
в ряд Тейлора).
Приведем основные разложения в ряд Маклорена:
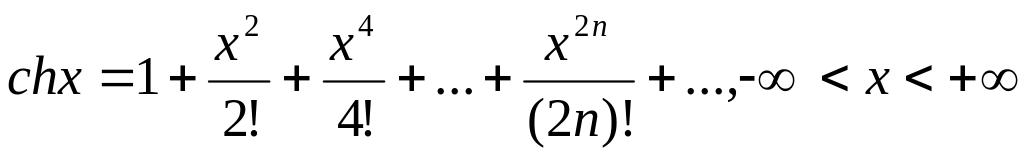
Биномиальный ряд
Причем
это последнее разложение при
является
абсолютно сходящимся рядом в граничных точках интервала,
т.е.
при х=-1
и при х=1;
при
ряд расходится при
х=-1
и условно сходится при при х=1;
при
ряд расходится на обеих границах
интервала (-1;1).
При разложении функции f(x) в ряд Тейлора по степеням х (когда ) преобразуют, если возможно, функцию f(x) к виду, допускающему использование основных разложений , а также сложение (вычитание) рядов, умножение ряда на число. Затем определяют область сходимости полученного ряда к функции f(x).
Замечание.
Если требуется разложить функцию в ряд
Тейлора по степеням
,
то сначала делают замену переменной
,
находят разложение по степеням t
и затем возвращаются к переменной х.
Пример. Разложить ln x в ряд по степеням (х-1).
Решение.
Имеем
,
то
(t=x-1),
где
область
сходимости есть полуинтервал
.
Задание 19. Разложить функции f(x) в ряд Тейлора по
степеням х.
Задача
3.
Решение. Данную рациональную функцию сначала разложим на элементарные дроби:
Так
как
-
Геометрические
прогрессии, сходящиеся соответственно
при
и
,
то окончательно имеем разложение
функции в ряд:
(16)
Областью
сходимости которого является пересечение
интервалов
.
Ответ: Формула (16) справедлива при -1<x<1.
Задача
4.
Решение.
Имеем
Пользуясь
биномиальным рядом при
:
Подставим
в разложении:
где
или
- бифакториал нечетных,
- бифакториал четных чисел. Последнее
равенство умножим почленно на
,
получаем искомое разложение f(x)
по степеням х:
,
с областью сходимости ряда
.
2.6. Приближенное вычисление определенных интегралов
Многие интегралы не могут быть выражены в конечном виде через элементарные функции. Одним из способов приближенного вычисления таких интегралов является разложение подынтегральной функции в степенной ряд и его почленное интегрирование. Известно, что функция, бесконечно дифференцируемая в интервале сходимости (-R,R), разлагается в этом интервале в сходящийся к ней степенной ряд Тейлора.
,
если в этом интервале сходимости где- остаточный член формулы Тейлора, записанный в форме Лагранжа, где - положительное число меньше 1.
Практически
степенные ряды для многих функций можно
найти формально, используя основные
разложения функций или формулу для
суммы членов геометрической прогрессии.
Итак, чтобы вычислить интеграл
с точностью ε, где
функция f(x) разложена в степенной ряд, имеющий радиус сходимости R>b, надо:
1)
Разложить функцию в степенной ряд по
степеням х:
и
определить его интервал сходимости.
Так как степенные ряды сходятся равномерно
на любом отрезке, лежащем внутри их
интервала сходимости, то на таком
отрезке можно интегрировать почленно
полученный ряд, используя формулу
Ньютона-Лейбница:
2) Вычислить сумму полученного числового ряда с
заданной точностью (оценивая остаток ряда). Заметим, что при интегрировании степенного ряда его интервал сходимости не изменяется.
Задание
20. Вычислить
интеграл с точностью
Задача
1.
Решение.
Разлагаем
функцию
в ряд Тейлора по степеням х (
,
=
).
Получаем ряд:
сходящийся также на всей числовой
прямой. Интегрируем ряд
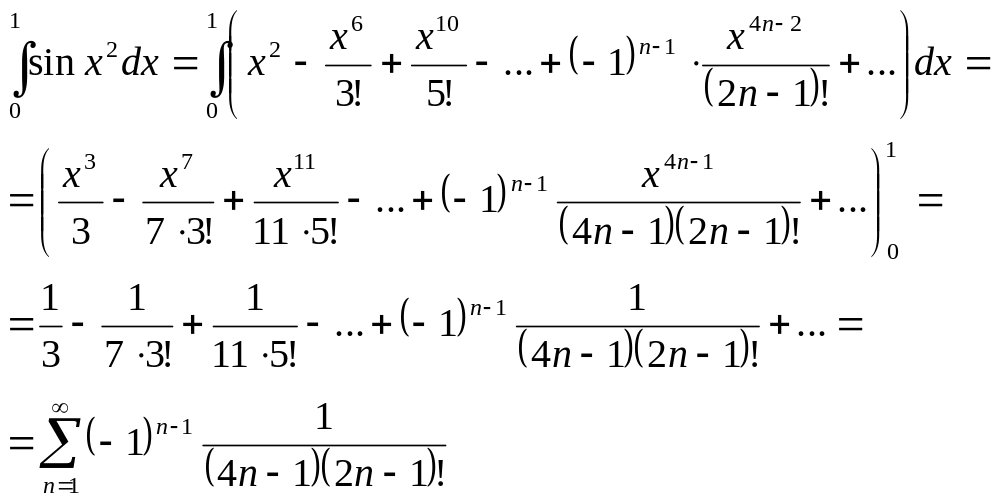
Оценим остаток ряда. Так как ряд знакочередующийся, члены которого убывают по абсолютной величине
при
и
,
то справедливо неравенство
(остаток
ряда
не превосходит
первого
из отброшенных членов). Если
,
то тем более
.
Поэтому, оценив неравенство
,
находим количество членов ряда,
необходимых для вычисления суммы с
заданной точностью ε. Практически
прикидывают, сколько надо взять членов
ряда для заданной точности. Здесь
достаточно взять первые два члена ряда,
т.к.
и, следовательно,
.
Вычисляем:
Ответ:
Задача
2.
Решение. Используем разложение
,
и
заменяя в нем
на
,
получаем ряд
,
сходящийся при всех . Интегрируем почленно полученный ряд
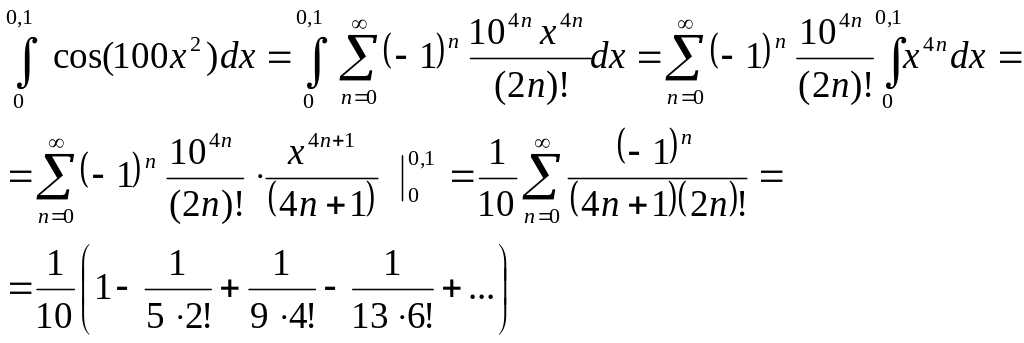Так
как
,
то оценивая это неравенство, получаем,
что для вычисления интеграла с точностью
достаточно
взять два члена ряда, ибо
.
Вычисляем
Ответ:
