2.4. Нахождение суммы функционального ряда

Рассмотрим некоторые приемы нахождения суммы

функционального ряда и области его сходимости к этой сумме.

Нахождение суммы ряда почленным интегрированием.

1. Пусть дан ряд вида . По признаку Коши или

признаку Даламбера область сходимости определяется неравенством . Если , то ряд - расходящийся.

Если , то ряд сходится условно (по признаку Лейбница). Следовательно, область сходимости находится из неравенства . Затем делаем замену в исходном ряде; получаем степенной ряд с областью сходимости . Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии со знаменателем

(12)

и очевидное равенство

(13)

Учитывая, что степенной ряд можно почленно интегрировать по любому отрезку , целиком принадлежащему интервалу сходимости, и используя формулу (13), получаем

Заметим, что так как ряд (12) сходится в граничной точке t=-1, то сумма ряда непрерывна в этой точке (справа) и . Далее вычисляем интеграл (с переменным верхним пределом), заменяем t на и получаем ответ.

2. Если дан ряд вида , то следует либо

применить теорему о почленном интегрировании степенного ряда дважды, либо разложить дробь на элементарные и вычислить сумму каждого ряда почленным интегрированием.

Пример. Найти сумму ряда и указать область

его сходимости к этой сумме.

Решение. Данный ряд степенной. Находим его интервал сходимости. По признаку Коши имеем

. Из неравенства находим . Исследуем поведение ряда в граничных точках. При - расходящийся гармонический ряд. При - условно сходящийся ряд по признаку Лейбница. Следовательно, данный ряд сходится при . Для нахождения суммы ряда сделаем замену . Получим геометрический ряд , сходящийся при . Используя равенство (13) и почленное интегрирование степенного ряда, получаем:

Ответ: для .

Замечание. Степенной ряд (10) сходится абсолютно и равномерно на всяком отрезке, лежащем внутри его интервала сходимости; ряд (10) можно почленно интегрировать и дифференцировать внутри его интервала сходимости , т.е. если то для имеем и

Задание 17. Найти сумму ряда и указать область сходимости к этой сумме.

Задача 1.

Решение.

Имеем .

Найдем сумму каждого из этих рядов в их области сходимости. Сначала рассмотрим ряд

.

Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии

, где , , и равенство (13).Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке , целиком принадлежащем интервалу сходимости, получаем первую сумму:

Т.к. ряд сходится в граничной точке х=-1, то его сумма непрерывна в этой точке: .Значит,

при всех . (14)

Аналогично находим вторую сумму с учетом (14):

Таким образом, сумма исходного ряда

Ответ: ,

Задача 2.

Решение. Находим область сходимости функционального ряда, применяя признак Даламбера

Область сходимости определяется неравенством , или . Решая его, получаем или . При имеем - расходящийся ряд (т.к. ~ ). Следовательно, ряд сходится при . Сделаем замену . Получим ряд с областью сходимости . Используя формулу (12): равенство (13): и почленное интегрирование на любом отрезке, принадлежащем области сходимости, получаем

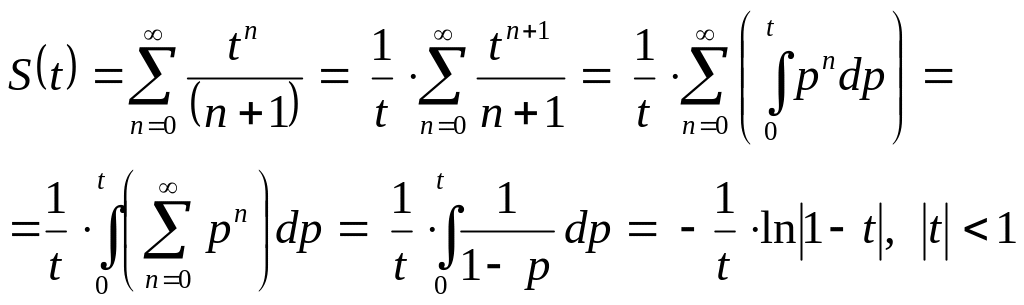
Заменяя t на , получаем сумму

Ответ: , .

Нахождение суммы ряда почленным дифференцированием.

I. Пусть дан ряд вида .

Сначала определяем область сходимости ряда, например, по признаку Коши. Получаем неравенство . Если , то ряд расходится, т.к. не выполнено необходимое

условие сходимости . Следовательно, область

сходимости определяется неравенством . Затем делаем замену и записываем ряд в виде суммы двух рядов . Для нахождения сумм этих рядов используем формулу суммы членов бесконечно убывающей геометрической прогрессии и очевидное равенство

.

Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя равенство

, получаем

Далее вычисляем производную, делаем замену

и записываем ответ.

II. Если дан ряд вида , то вычисляем сумму трех рядов , и , причем при вычислении суммы ряда применяем теорему о почленном дифференцировании степенного ряда дважды.

Задание 18. Найти сумму ряда и указать область

сходимости ряда к этой сумме.

Задача 3.

Решение. а). Находим область сходимости данного ряда по признаку Даламбера

Отсюда . В граничных точках ряд расходится, т.к. не выполнено необходимое условие сходимости. Итак, ряд сходится (и притом абсолютно) в интервале (-1;1).

б). Делаем в исходном ряде замену и записываем в виде суммы двух рядов

Для нахождения S(t) достаточно найти суммы рядов

и

.

Учитывая, что степенной ряд можно почленно

дифференцировать в любой точке интервала сходимости,

получаем

.

И

в) Заменяя на , получаем

Ответ:

Задача 4.

Решение. По признаку Коши интервал сходимости

степенного ряда определяется неравенством , т.е. ряд сходится в интервале (-1;1). Для нахождения суммы ряда достаточно представить ряд в виде суммы трех рядов и найти суммы рядов:

,

где применили один раз почленное дифференцирование по x;

.

Т.к. выше найденная на предыдущем шаге сумма ряда

, то еще раз применив почленное дифференцирование по x к ряду; , получаем .Таким образом, сумма исходного ряда равна

.

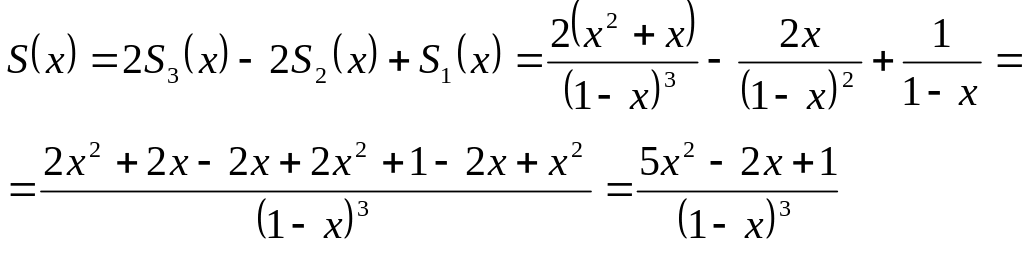Ответ: ,