
- •Введение
- •1. Числовые ряды
- •1.1. Основные понятия и определения
- •1.2. Нахождение суммы знакоположительного ряда
- •1.3. Исследование сходимости знакоположительных рядов
- •1.4. Знакопеременные ряды. Признак Лейбница для знакочередующихся рядов
- •1.5. Приближенное вычисление суммы знакочередующегося ряда
- •2. Функциональные ряды
- •2.1. Основные теоретические сведения
- •2.2. Нахождение области сходимости функциональных рядов
- •2.3. Интервал и радиус сходимости степенного ряда
- •2.4. Нахождение суммы функционального ряда
- •2.5. Разложение функций в степенной ряд Тейлора
- •2.6. Приближенное вычисление определенных интегралов
- •Заключение
- •Библиографический список
- •394026 Воронеж, Московский просп., 14
2.3. Интервал и радиус сходимости степенного ряда
Степенным рядом называется функциональный ряд вида
![]() ,
(10)
,
(10)
где
коэффициенты
![]() -
действительные числа.
-
действительные числа.
Основное свойство степенных рядов состоит в том, что если ряд (10) сходится при , то он сходится ( и притом абсолютно) при всяком значении х, удовлетворяющем неравенству
![]() (теорема
Абеля). Следствием теоремы Абеля является
существование для всякого степенного
ряда (10) интервала сходимости
(теорема
Абеля). Следствием теоремы Абеля является
существование для всякого степенного
ряда (10) интервала сходимости
![]() с центром в точке х=а,
внутри которого ряд (10) сходится абсолютно
; при
с центром в точке х=а,
внутри которого ряд (10) сходится абсолютно
; при
![]() ряд (10) расходится. Радиус
сходимости R
(т.е. половина длины интервала сходимости)
может быть в частных случаях равен также
0 и ∞. В конечных точках
ряд (10) расходится. Радиус
сходимости R
(т.е. половина длины интервала сходимости)
может быть в частных случаях равен также
0 и ∞. В конечных точках
![]() интервала сходимости возможна как
сходимость, так и расходимость ряда
(10). Интервал сходимости определяют
обычно с помощью признаков Даламбера
или Коши, применяя их к ряду, составленному
из абсолютных величин членов исходного
ряда . Но если
интервала сходимости возможна как
сходимость, так и расходимость ряда
(10). Интервал сходимости определяют
обычно с помощью признаков Даламбера
или Коши, применяя их к ряду, составленному
из абсолютных величин членов исходного
ряда . Но если
![]() или
или
![]() ,
(11)
,
(11)
где
![]() и
и
![]() - коэффициенты соответственно n-го
и (n+1)-го
членов ряда (10), то радиус сходимости
ряда (10) определяется по формуле
- коэффициенты соответственно n-го
и (n+1)-го
членов ряда (10), то радиус сходимости
ряда (10) определяется по формуле
![]() .
Однако пользоваться формулами (11) следует
весьма осторожно. Если L=0,
то R=∞
и ряд (10) сходится при
.
Однако пользоваться формулами (11) следует
весьма осторожно. Если L=0,
то R=∞
и ряд (10) сходится при
![]() .
Если L=∞,
то R=0
и ряд (10) расходится при любом х, кроме
х=0.
.
Если L=∞,
то R=0
и ряд (10) расходится при любом х, кроме
х=0.
Пример 1. Найти радиус и интервал сходимости
степенного
ряда
![]()
Решение.
Имеем коэффициенты ряда
![]() .
Найдем число L
(см. формулы 11)
.
Найдем число L
(см. формулы 11)
![]() .
Следовательно, радиус сходимости R=5.
Интервал сходимости ряда
.
Следовательно, радиус сходимости R=5.
Интервал сходимости ряда
![]() с центром в точке
с центром в точке
![]() или
или
![]() есть
есть
![]() .
Исследуем поведение ряда в концевых
точках интервала:
.
Исследуем поведение ряда в концевых
точках интервала:
При
х=8:
![]() -
расходящийся гармонический ряд
-
расходящийся гармонический ряд
При
х=-2:
![]() - условно сходящийся (по Лейбницу).
- условно сходящийся (по Лейбницу).
Ответ:
R=5;
![]() .
.
Пример 2. Исследовать сходимость ряда
![]()
Решение.
Общий член
ряда имеет коэффициент
![]()
Находим
по формуле (11) число
![]() .
.
Т.е.,
![]() .
Значит, ряд расходится при
.
Значит, ряд расходится при
![]() ,
кроме х=0. В этом случае говорят, что ряд
всюду расходится.
,
кроме х=0. В этом случае говорят, что ряд
всюду расходится.
Задание 14. Найти область сходимости степенного ряда.
Задача
1.
![]()
Решение.
Имеем коэффициенты ряда
![]() ,
,
![]() .
Находим число L
по одной из формул (11):
.
Находим число L
по одной из формул (11):
 ,
(т.к.
,
(т.к.
![]() ~
~![]() при бесконечно малых
).
Значит, радиус сходимости
при бесконечно малых
).
Значит, радиус сходимости
![]() ,
интервал сходимости
,
интервал сходимости
![]() с центром в точке
с центром в точке
![]() .
Откуда получаем
.
Откуда получаем
![]() ,
или
,
или
![]() .
В концевых точках интервала (-8;-2) исследуем
поведение ряда: При х=-2 имеем ряд
.
В концевых точках интервала (-8;-2) исследуем
поведение ряда: При х=-2 имеем ряд
![]() - расходящийся, т.к.
- расходящийся, т.к.
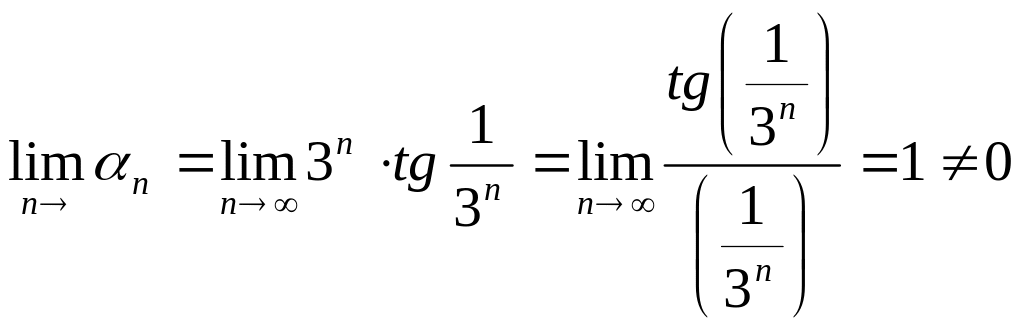 .
При х=-8 имеем знакочередующийся ряд
.
При х=-8 имеем знакочередующийся ряд
![]() ,
который также расходится, ибо не выполнено
условие
,
который также расходится, ибо не выполнено
условие
![]() .
.
Ответ: Интервал сходимости (-8;-2), R=3.
Задача
2.
![]()
Решение.
Область
сходимости данного степенного ряда
будем находить по одной из формул (9),
т.к. этот ряд содержит члены только с
нечетными степенями (х-7) и пользоваться
напрямую формулами (11) нельзя, поэтому
что бесконечно много коэффициентов
![]() обращается в ноль и пределы в правых
частях формул (11) не существуют. Имеем
обращается в ноль и пределы в правых
частях формул (11) не существуют. Имеем
![]() .
.
Находим
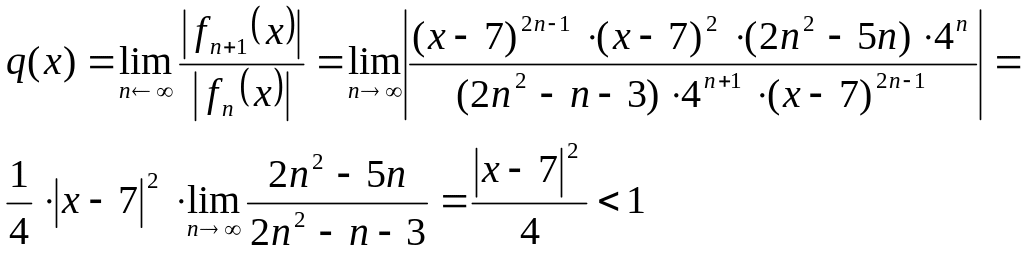
должно быть для сходимости ряда по признаку Даламбера.
Решая
неравенство
![]() ,
получаем
,
получаем
![]() ,
или
,
или
![]() ,
откуда интервал сходимости степенного
ряда
,
откуда интервал сходимости степенного
ряда
(5;9)
с центром в точке
![]() и радиусом R=2.
Рассмотрим поведение ряда в концевых
точках: При х=9 получаем знакоположительный
числовой ряд
и радиусом R=2.
Рассмотрим поведение ряда в концевых
точках: При х=9 получаем знакоположительный
числовой ряд
![]() ,
где общий член
,
где общий член
![]() ~
~![]() и по второму (предельному) признаку
сравнения сходится, ибо сходится ряд
и по второму (предельному) признаку
сравнения сходится, ибо сходится ряд
![]() (p=2>1).
(p=2>1).
При х=5 получаем ряд
![]() с
общим членом
с
общим членом
![]() ,
который также сходится.
,
который также сходится.
Ответ:
Интервал сходимости
![]() .
.
