2.2. Нахождение области сходимости функциональных рядов
Для определения области сходимости функционального
ряда (8) достаточно применить к этому ряду известные признаки сходимости, считая аргумент х фиксированным.
Например, при использовании признаков Даламбера или Коши поступают так:
Находят q(x) по одной из формул (если пределы
существуют)
или
(9)
Решают неравенство q(x)<1 (т.к. по признакам
Даламбера и Коши ряд сходится при q<1 и расходится при q>1). В результате находим интервал сходимости.
Исследуется поведение ряда в концевых точках
интервала сходимости.
Пример. Найти область сходимости ряда
Решение. Рассмотрим три случая
Если
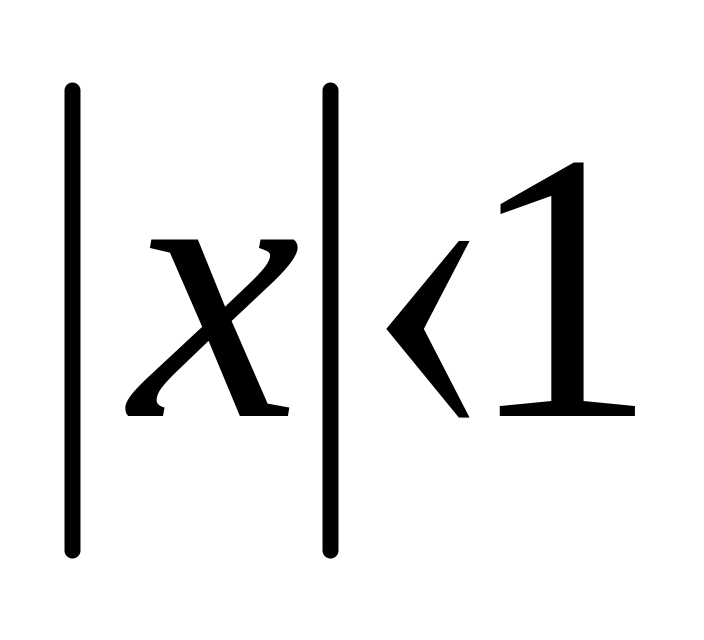, то
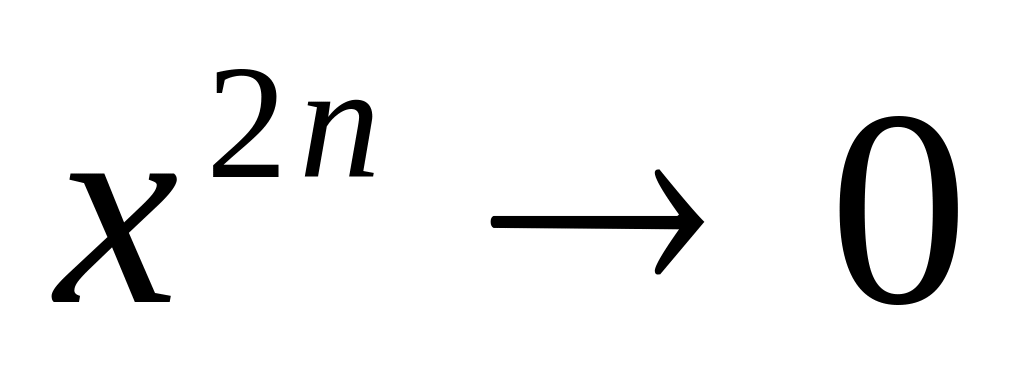при
и
.
Необходимый признак сходимости ряда
не выполнен. Следовательно, ряд расходится
при -1<x<1.
Если
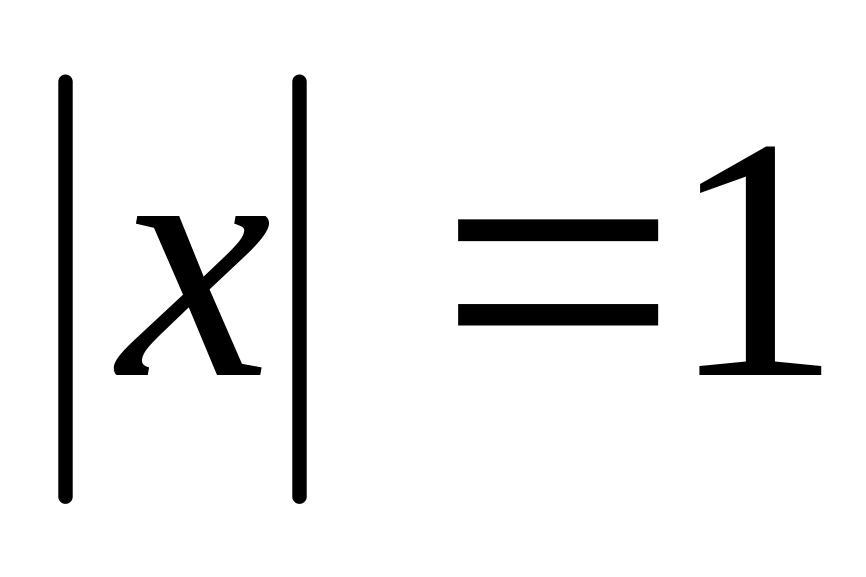, то также получаем расходящийся ряд
Если
,
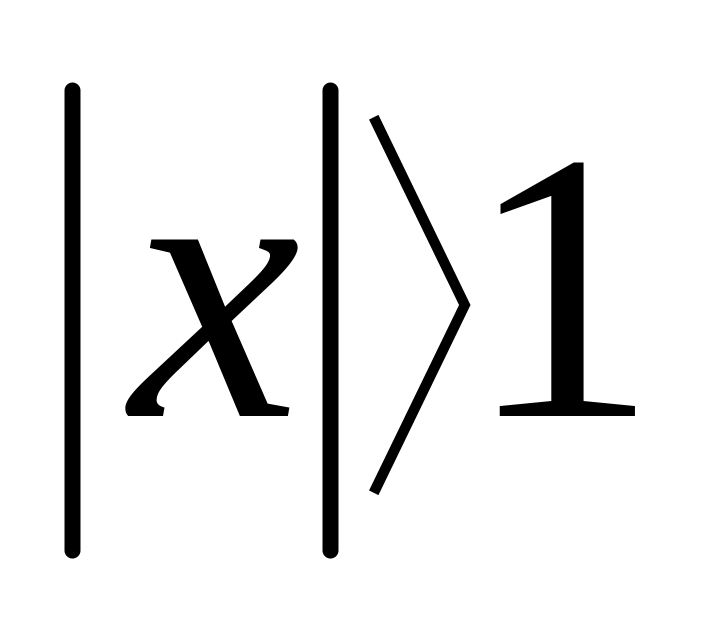то применим первый признак сравнения
,
где сходящийся ряд
представляет
собой сумму бесконечно убывающей геометрической
прогрессии
со знаменателем
,
т.е.
.
Итак, исследуемый ряд сходится при
;
его область сходимости
Задания (11-13).
Задача 1. Найти область сходимости функционального ряда
Решение. Все члены данного ряда положительны при для каждого фиксированного значения х.
Сравним
данный ряд с рядом
.
Это можем сделать согласно второму
(предельному) признаку сравнения, т.к.
,
т.е. fn(x)
и
-
эквивалентные бесконечно малые при
,
ибо
.Ряд
будет сходиться при
(как обобщенный гармонический ряд
,
сходящийся при p>1
и расходящийся при
).
Откуда следует
.
Ответ:
Область сходимости ряда интервал
Задача
2.
Решение. Признак Даламбера в данном случае ответа не дает, т.к.
.
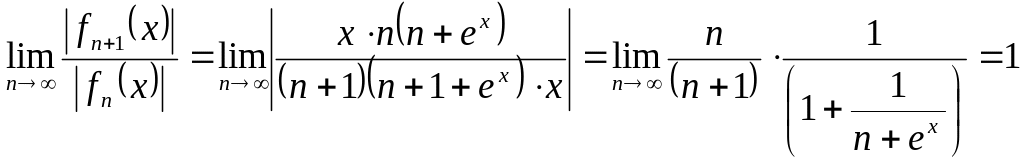Используем второй (предельный) признак сравнения, где для сравнения возьмем сходящийся ряд (р=2>1).
При
любом фиксированном
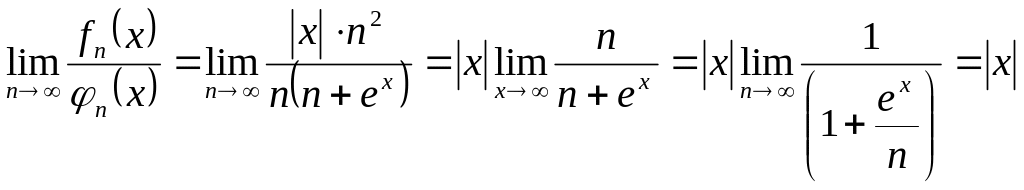конечное
число и оба ряда сходятся при
.
При х=0 имеем сходящийся ряд «чистых»
нулей.
Ответ:
Область сходимости ряда
Задача
3.
Решение. Для того, чтобы применить признак Даламбера, находим q(x) по формуле (9):
.
Область сходимости функционального ряда дают
значения
х, удовлетворяющие неравенству
.
При
имеем сходящийся ряд
(р=3>1),
При
имеем абсолютно сходящийся ряд
.
Значит, область абсолютной сходимости
исходного ряда находим, решая неравенства
.
Получаем
(с
учетом периодичности функции, Т=
).
Откуда следует, что
.
Таким образом, областью сходимости функционального
ряда
будет объединение отрезков
,
где
Задача
4.
Решение. Используем признак Коши. Находим
,
ибо
(с.м. пункт 1.3, замечания 2). Ряд сходится
при q(x)<1
по Коши, откуда
,
или
.
Итак,
решение системы тригонометрических
неравенств дает интервалы абсолютной
сходимости функционального ряда. В
граничных точках при
имеем числовые ряды
и
,
сходящиеся абсолютно. Область абсолютной
сходимости данного ряда находим из
системы неравенств:
.
Откуда получаем и
.
Т.е. область абсолютной сходимости
данного ряда является объединение
отрезков
,
.
Задача
5.
Решение.
Данный ряд знакоположительный при
.
Находим q(x)
по формуле (9):
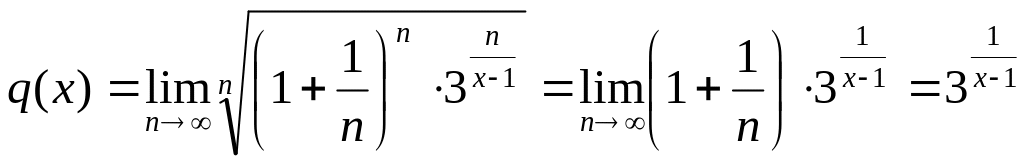
Решаем
неравенство q(x)<1:
,
или
;
Получаем
,
откуда x-1<0,
т.е. ряд сходится при x<1.
В граничной точке х=1 общий член
не имеет смысла. Итак, областью сходимости
ряда является интервал
.
Задача
6.
Решение.
Дан знакочередующийся ряд. Обозначим
показатель степени
,
причем
при
и
при
.
Рассмотрим два случая: Если
,
то имеем расходящийся ряд
.
Если
,
то имеем ряд
- условно сходящийся по признаку Лейбница:
1)
,
т.е.
;
2)
Но
ряд из модулей
- обобщенный
гармонический, сходящийся при и расходящийся при
.
Значит, рассматриваемый ряд
сходится
абсолютно
при
>1,
т.е.
,
откуда
следует
,
или
- область абсолютной
сходимости
ряда, т.е. при
и
.
При
0<
,
т.е. при
- область условной сходимости ряда, т.е.
при
.
Ответ: Область абсолютной сходимости –
,
область условной сходимости –
Задача
7.
Решение. Применим признак Даламбера. Найдем
Для сходимости ряда, согласно признаку, достаточно,
чтобы
q(x)<1.
Решаем неравенство
,
или
.
Откуда
имеем
или
.
Получаем сходимость при
и
.
При
числовой ряд
расходится
и при
числовой
ряд
расходится, т.к. необходимый признак сходимости не выполняется.
Ответ:
Область сходимости
