ГОУВПО

“Воронежский государственный технический университет”

Кафедра высшей математики и физико-математического моделирования

РЯДЫ ФУРЬЕ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для студентов специальности

230201 “Информационные системы и технологии”

очной формы обучения

Воронеж 2011

Составители: канд. физ.- мат. наук В.В. Дежин,

д-р техн. наук М.Л. Лапшина

УДК 517.2. (07)

Ряды Фурье: методические указания для студентов специальности 230201 “Информационные системы и технологии” очной формы обучения / ГОУВПО “Воронежский государственный технический университет”; Сост. В.В. Дежин, М.Л. Лапшина. Воронеж, 2011. 28 с.

Методические указания содержат краткий теоретический материал и большое количество подробно разобранных задач, задачи для самостоятельного решения, предназначены для практических занятий на втором курсе.

Методические указания подготовлены на магнитном носителе в текстовом редакторе Microsoft Word, файл ряды Фурье.doc.

Ил. 2. Библиогр.: 3 назв.

Рецензент д-р физ.-мат. наук, проф. В.Д. Репников

Ответственный за выпуск д-р физ.-мат. наук, проф. И.Л. Батаронов

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

© ГОУВПО “Воронежский государственный

технический университет”, 2011

Достаточные признаки разложимости в ряд Фурье

_{Первые труды Фурье относятся к алгебре. Уже в лекциях 1796 он изложил теорему о числе действительных корней алгебраического уравнения, лежащих между данными границами, названную его именем; полное решение о числе действительных корней алгебраического уравнения было получено в 1829 Ж. Ш. Ф. Штурмом. В 1818 Фурье исследовал вопрос об условиях применимости разработанного Ньютоном метода численного решения уравнений, не зная об аналогичных результатах, полученных в 1768 французским математиком Ж.Р. Мурайлем. Итогом работ Фурье по численным методам решения уравнений является «Анализ определённых уравнений», изданный посмертно в 1831. Основной областью занятий Фурье была математическая физика. В 1807 и 1811 он представил Парижской Академии Наук свои первые открытия по теории распространении тепла в твёрдом теле, а в 1822 опубликовал известную работу «Аналитическая теория теплоты», сыгравшую большую роль в последующей истории математики. Это – математическая теория теплопроводности. В силу общности метода эта книга стала источником всех современных методов математической физики. В этой работе Фурье вывел дифференциальное уравнение теплопроводности и развил идеи, в самых общих чертах намеченные ранее Д. Бернулли, разработал для решения уравнения теплопроводности при тех или иных заданных граничных условиях метод разделения переменных (метод Фурье), который он применял к ряду частных случаев (куб, цилиндр и др.). В основе этого метода лежит представление функций тригонометрическими рядами Фурье. Ряды Фурье теперь стали хорошо разработанным средством в теории уравнений в частных производных при решении граничных задач.}

Многие процессы, происходящие в природе и технике, обладают свойством повторяться через определённые промежутки времени. Такие процессы называются периодическими. Периодические процессы описываются периодическими функциями. Простейшими периодическими функциями с периодом являются и . Легко показать, что функции и имеют период .

Вычислим несколько интегралов, которые нам понадобятся в дальнейшем, k и n–натуральные числа

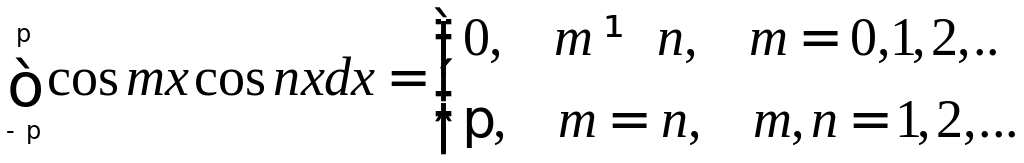
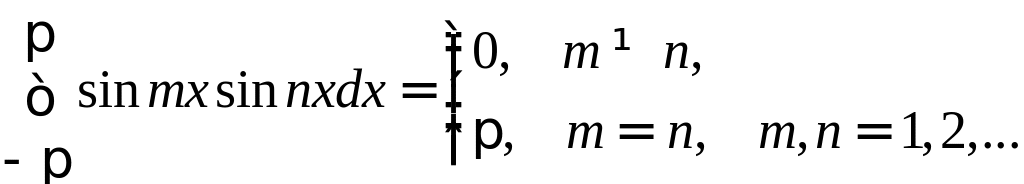
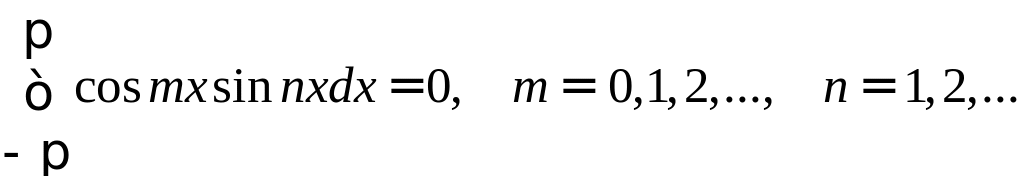
Справедливость этих равенств вытекает из применения к подынтегральному выражению тригонометрических формул.

Т.к. функция f(x) непрерывна на отрезке [-; ], то существует интеграл

.

Такой результат получается в результате того, что .

Получаем: 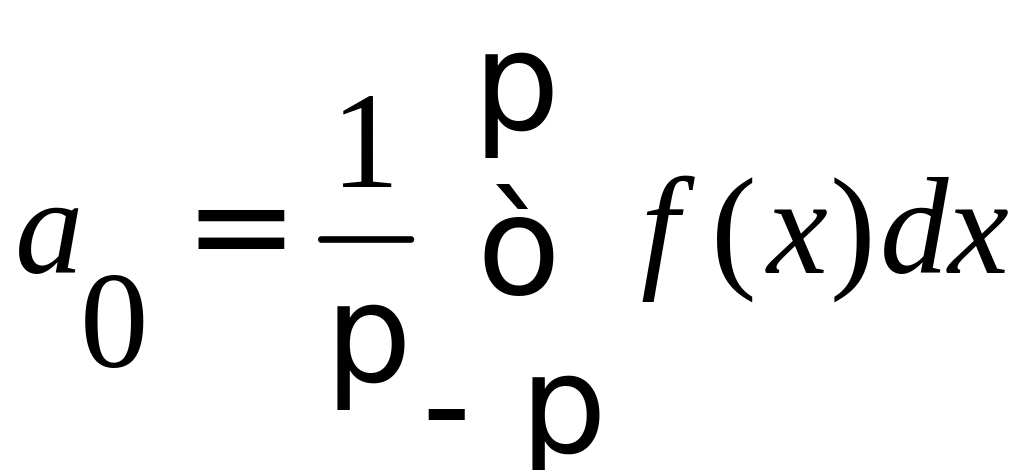. Далее умножаем выражение разложения функции в ряд на cosnx и интегрируем в пределах от - до .

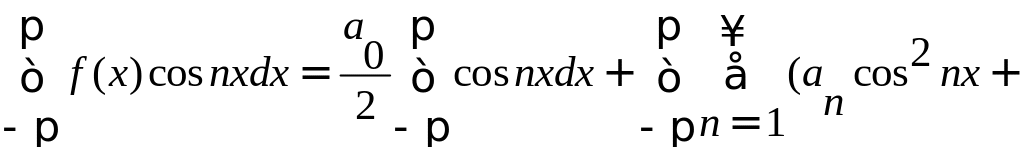
Отсюда получаем:

Аналогично умножаем выражение разложения функции в ряд на sinnx и интегрируем в пределах от - до . Получаем:

Выражение для коэффициента а₀ является частным случаем для выражения коэффициентов a_n.

Таким образом, если функция f(x) – любая периодическая функция периода 2, непрерывная на отрезке [-; ] или имеющая на этом отрезке конечное число точек разрыва первого рода, то коэффициенты

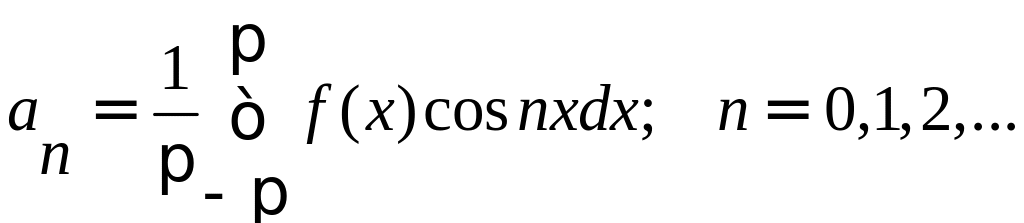
существуют и называются коэффициентами Фурье для функции f(x).

Определение. Рядом Фурье для функции f(x) называется тригонометрический ряд, коэффициенты которого являются коэффициентами Фурье. Если ряд Фурье функции f(x) сходится к ней во всех ее точках непрерывности, то говорят, что функция f(x) разлагается в ряд Фурье.

Теорема. (Теорема Дирихле) Если функция f(x) имеет период 2 и на отрезке [-;] непрерывна или имеет конечное число точек разрыва первого рода, и отрезок [-;] можно разбить на конечное число отрезков так, что внутри каждого из них функция f(x) монотонна, то ряд Фурье для функции f(x) сходится при всех значениях х, причем в точках непрерывности функции f(x) его сумма равна f(x), а в точках разрыва его сумма равна 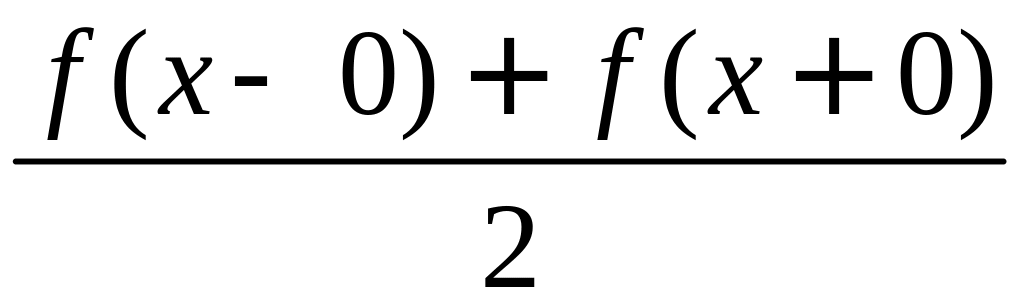, т.е. среднему арифметическому предельных значений слева и справа. При этом ряд Фурье функции f(x) сходится равномерно на любом отрезке, который принадлежит интервалу непрерывности функции f(x).

Пример: Разложить в ряд Фурье функцию с периодом

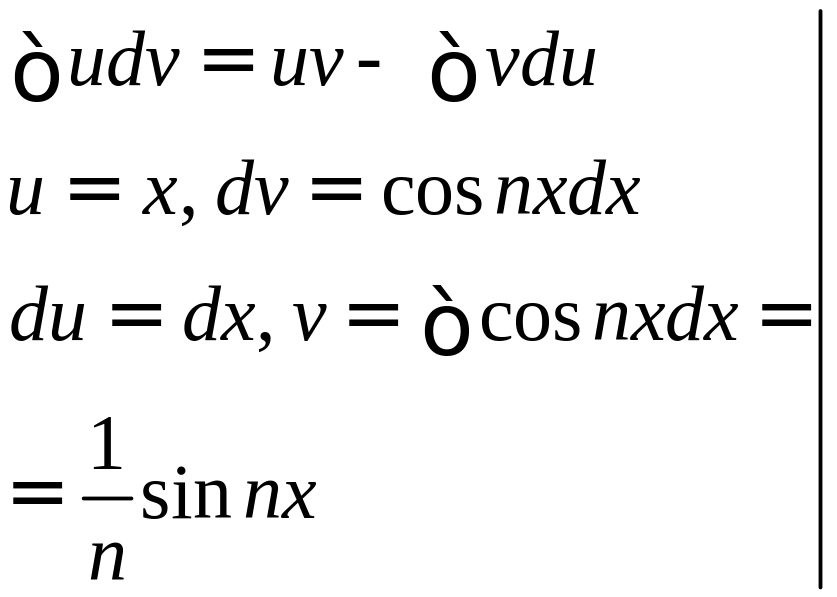
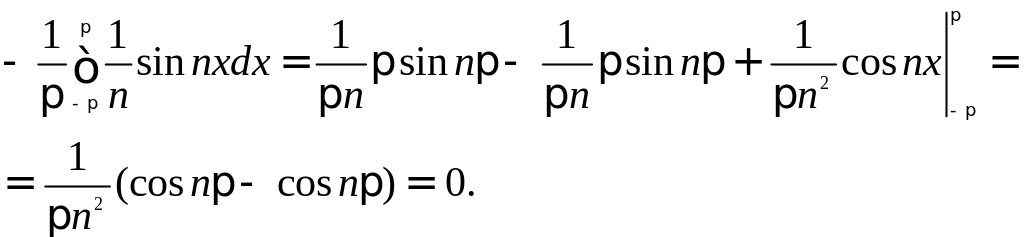
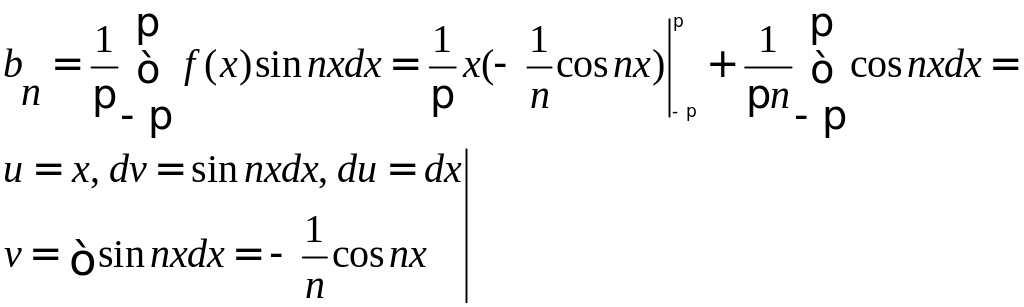
Получаем

Замечание: Нетрудно показать, что если функция f(x) имеет период , то

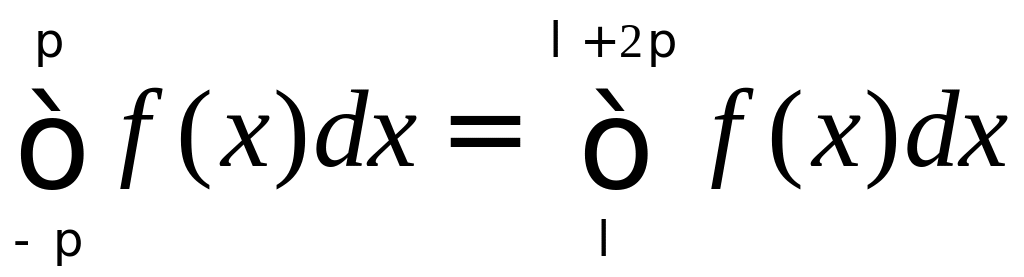, где l – любое число.

Функция f(x), для которой выполняются условия теоремы Дирихле называется кусочно–монотонной на отрезке [-;].

Ряд Фурье для четных и нечетных функций

Отметим следующие свойства четных и нечетных функций:

1) .

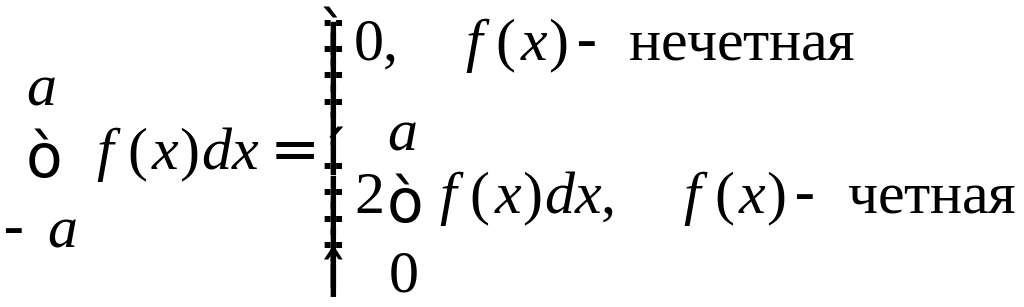2) Произведение двух четных и нечетных функций является четной функцией.

3) Произведение четной и нечетной функций – нечетная функция.

Справедливость этих свойств может быть легко доказана исходя из определения четности и нечетности функций.

Если f(x) – четная периодическая функция с периодом 2, удовлетворяющая условиям разложимости в ряд Фурье, то можно записать:

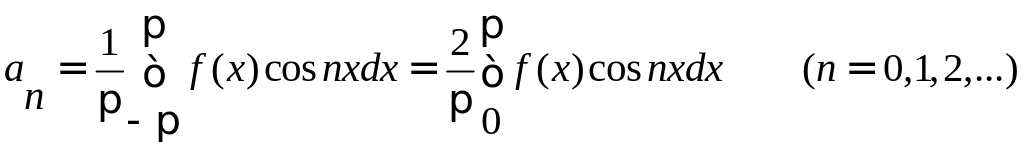
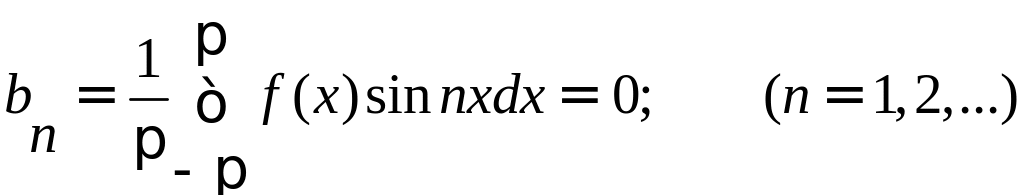
Таким образом, для четной функции ряд Фурье записывается:

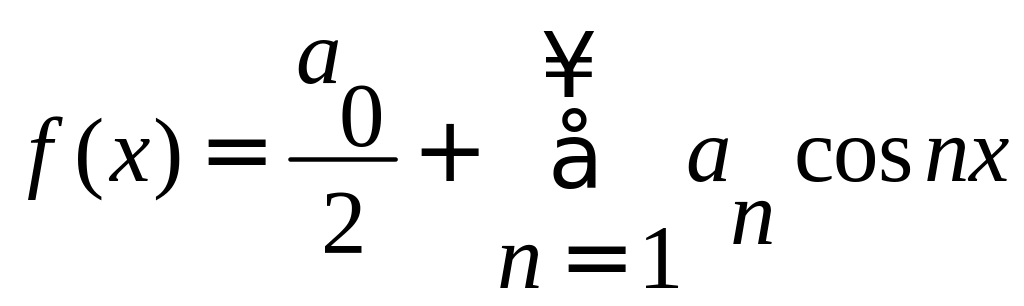
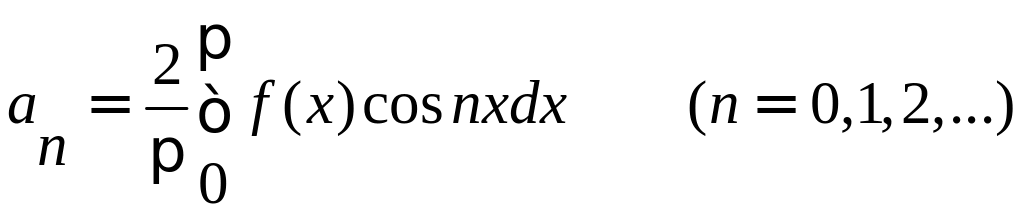
Аналогично получаем разложение в ряд Фурье для нечетной функции:

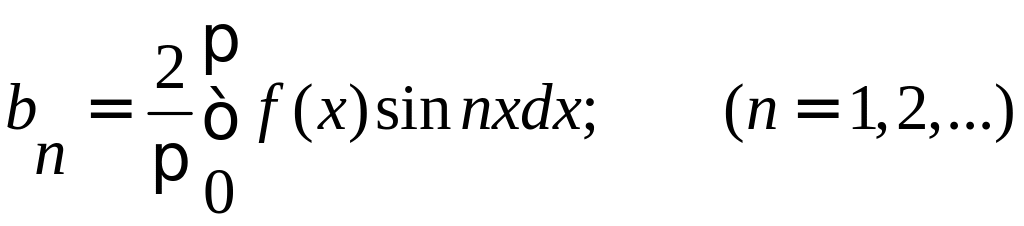
Пример. Разложить в ряд Фурье периодическую функцию с периодом T = 2 на отрезке [-; ].

Заданная функция является нечетной, следовательно, коэффициенты Фурье ищем в виде:

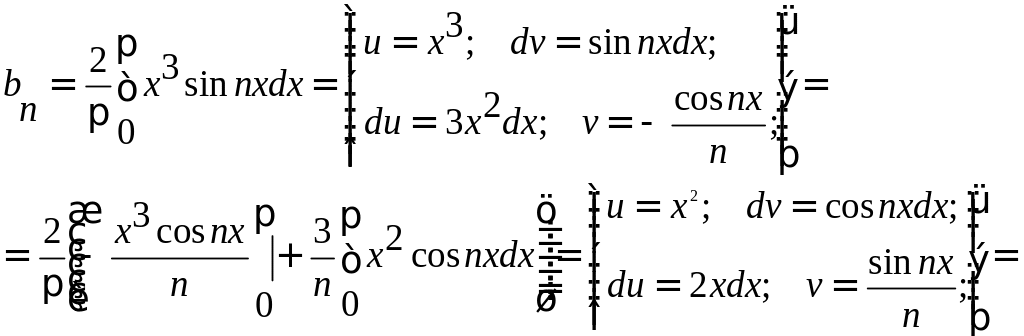
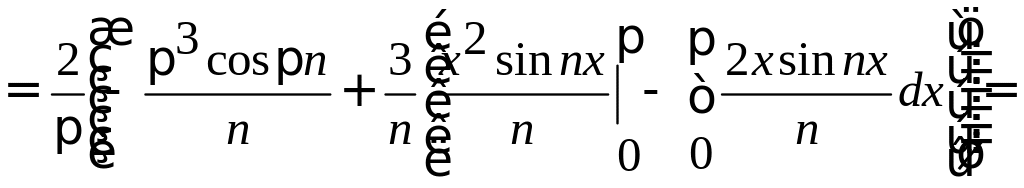
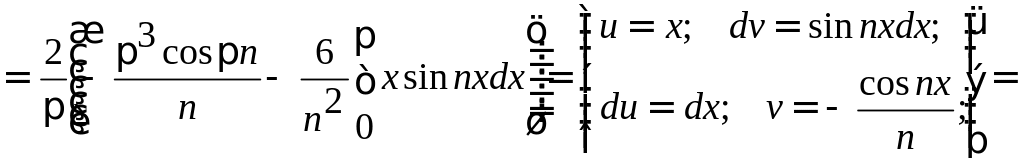
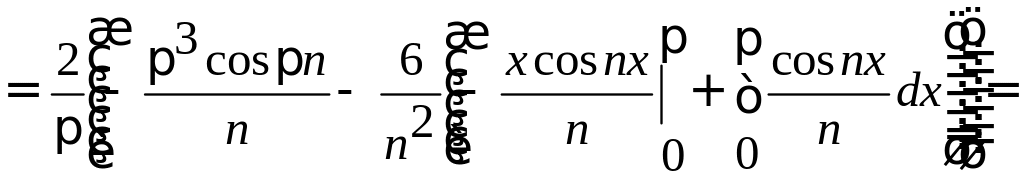
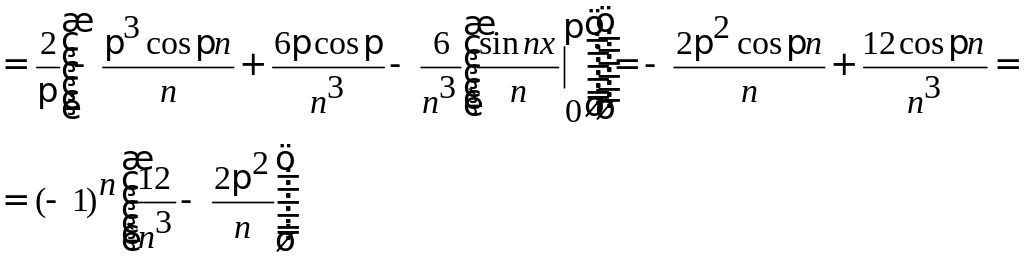
Получаем:

.

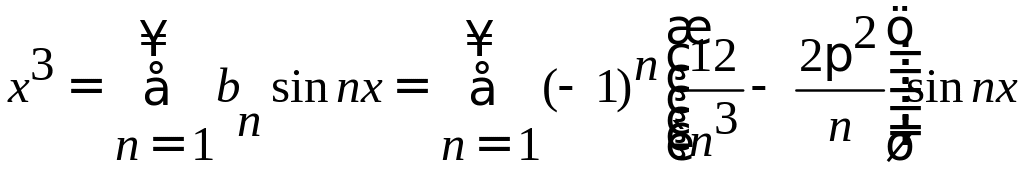Построим графики (рисунок 1) заданной функции и ее разложения в ряд Фурье, ограничившись первыми четырьмя членами ряда.

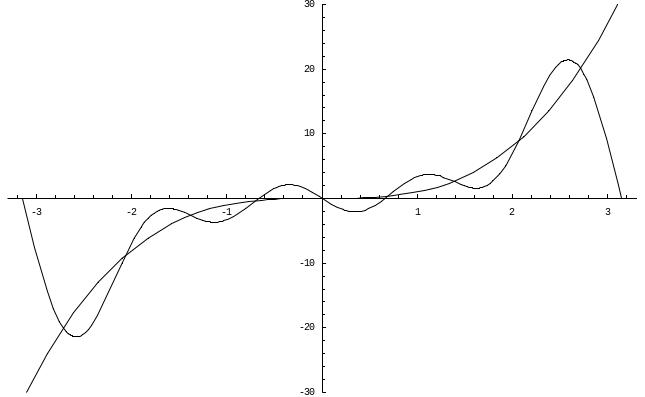
Рисунок 1

Пример: Разложить в ряд Фурье функцию с периодом . Данная функция четная, поэтому

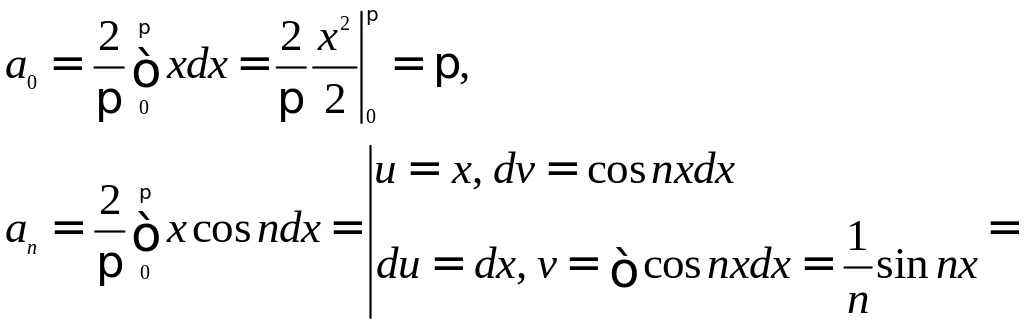
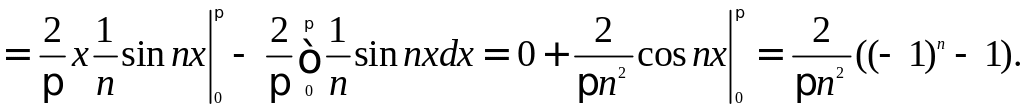
Заметим, что

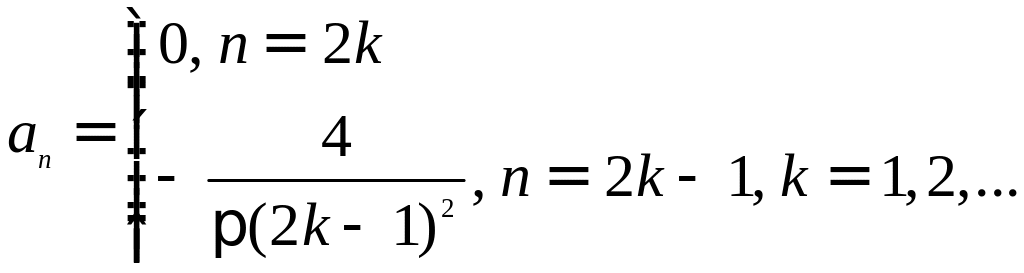
Получим ряд Фурье:

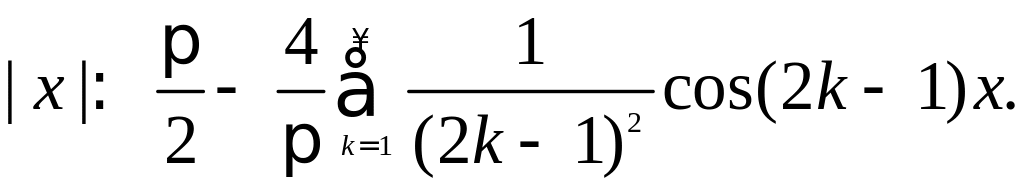
Разложение в ряд Фурье непериодических функций

Если функция задана на всей числовой оси и непериодическая, то её нельзя разложить в ряд Фурье, так как сумма тригонометрического ряда является периодической функцией.

Рассмотрим непериодическую непрерывную функцию на промежутке и построим ряд Фурье, который имел бы её своей суммой в этом интервале. Для этого рассмотрим вспомогательную функцию с периодом такую, что при . Разложив в ряд Фурье функцию , мы получили тем самым разложение на .

Если функция задана только в промежутке , то для разложения её в ряд Фурье на этом промежутке, нужно сначала продолжить её каким–то образом на промежуток , а затем продолжить периодически с периодом на всю числовую ось. Чаще всего на промежуток функцию продолжают чётным или нечётным образом.

Пример. Разложить функцию заданную на [0; 1] в ряд по синусам. Продолжим данную функцию в интервал (-1, 0) нечётным образом, а затем продолжим периодически с периодом 2e=2 на всю числовую ось. Тогда

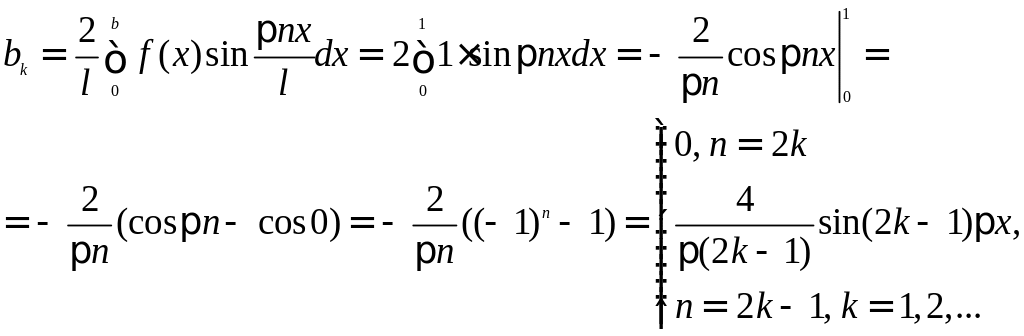
Получаем ряд Фурье: .

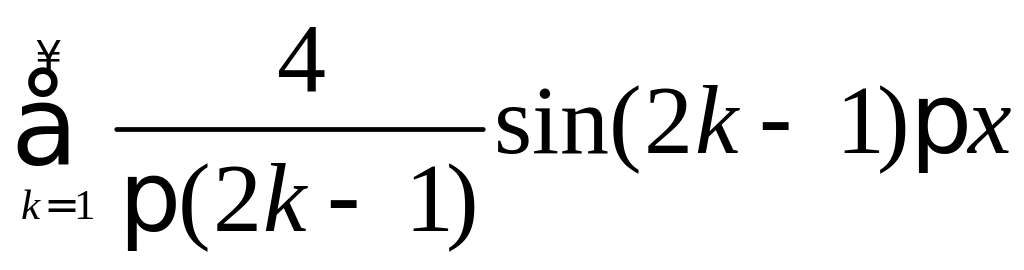Ряды Фурье для функций любого периода

Ряд Фурье для функции f(x) периода Т = 2l, непрерывной или имеющей конечное число точек разрыва первого рода на отрезке [-l, l] имеет вид:

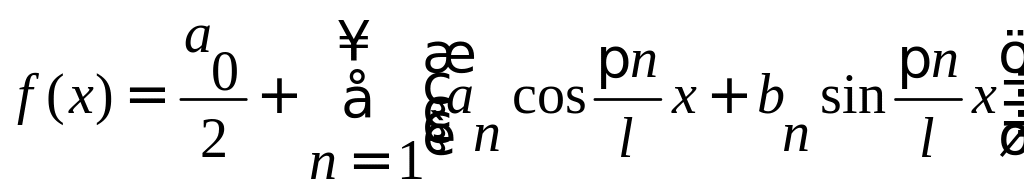
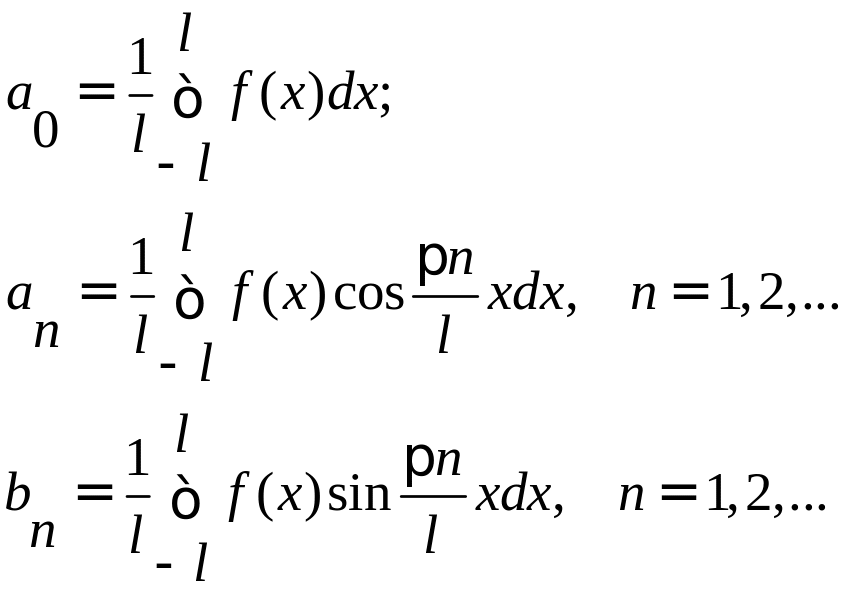
Для четной функции произвольного периода разложение в ряд Фурье имеет вид:

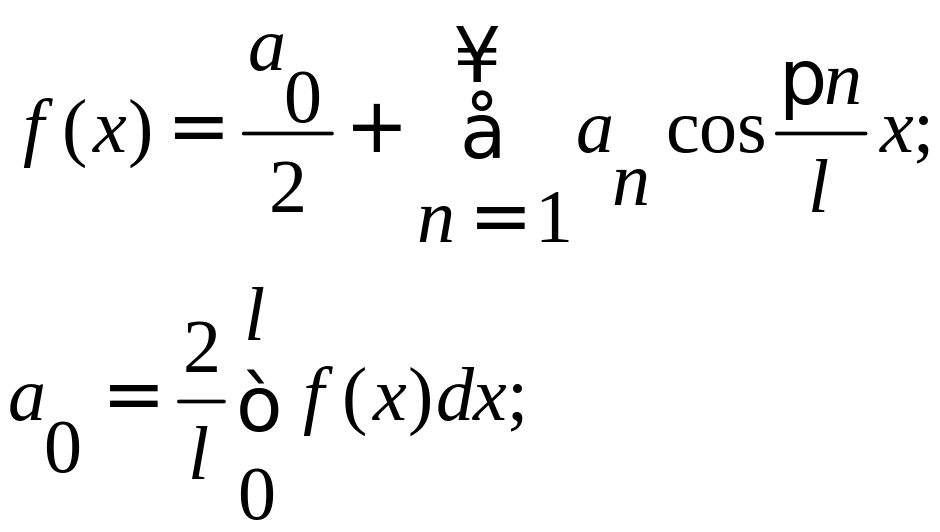
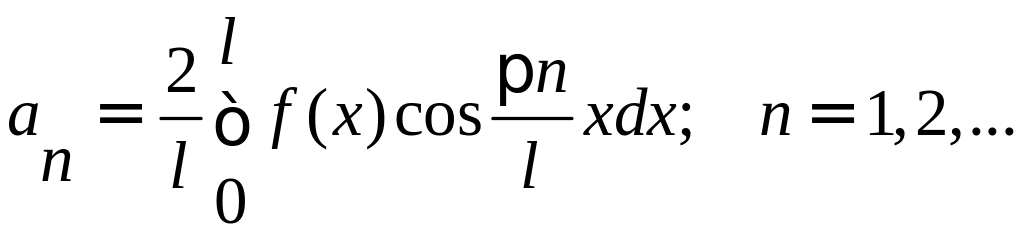
Для нечетной функции:

Ряд Фурье по ортогональной системе функций

Определение. Функции (х) и (х), определенные на отрезке [a, b], называются ортогональными на этом отрезке, если

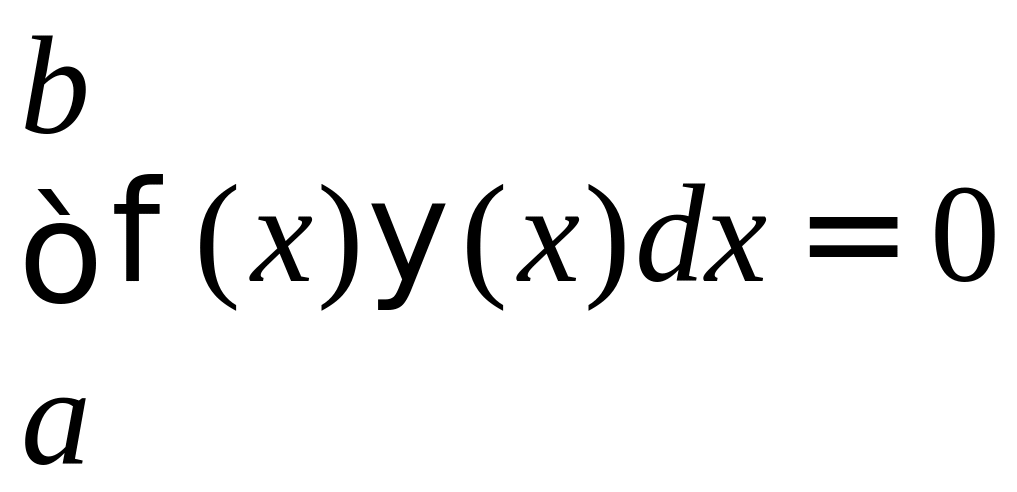
Определение. Последовательность функций ₁(x), ₂(x), …, _n(x), непрерывных на отрезке [a, b], называется ортогональной системой функций на этом отрезке, если все функции попарно ортогональны.

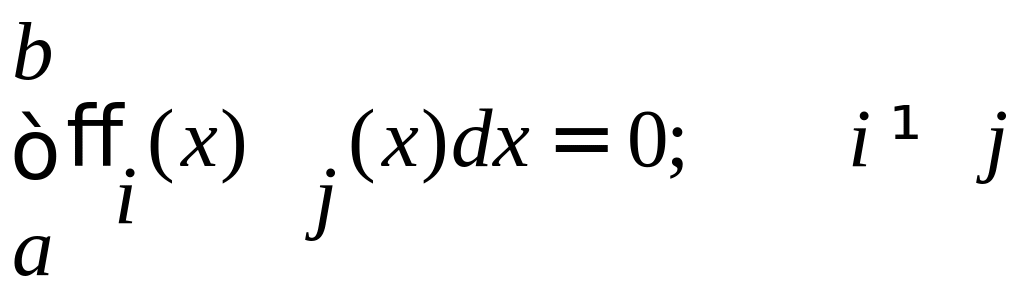
Отметим, что ортогональность функций не подразумевает перпендикулярности графиков этих функций.

Определение. Система функций называется ортогональной и нормированной (ортонормированной), если

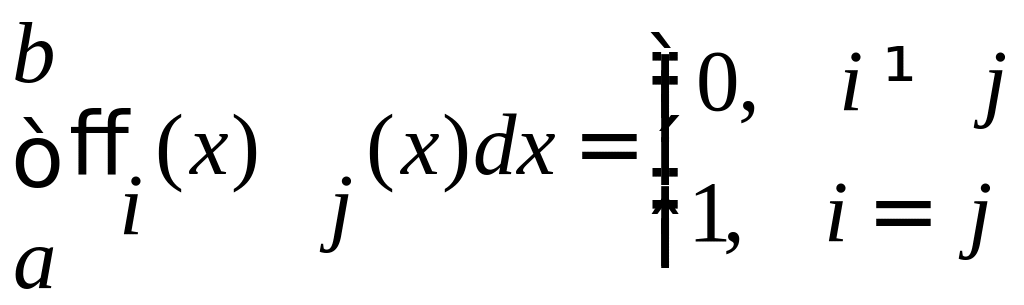
Определение. Рядом Фурье по ортогональной системе функций ₁(x), ₂(x), …,_n(x) называется ряд вида: 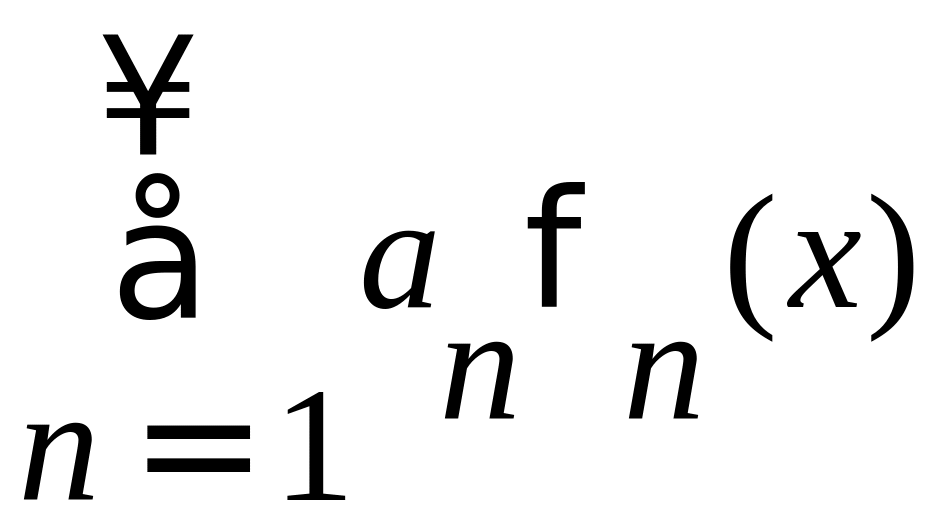коэффициенты которого определяются по формуле:

,

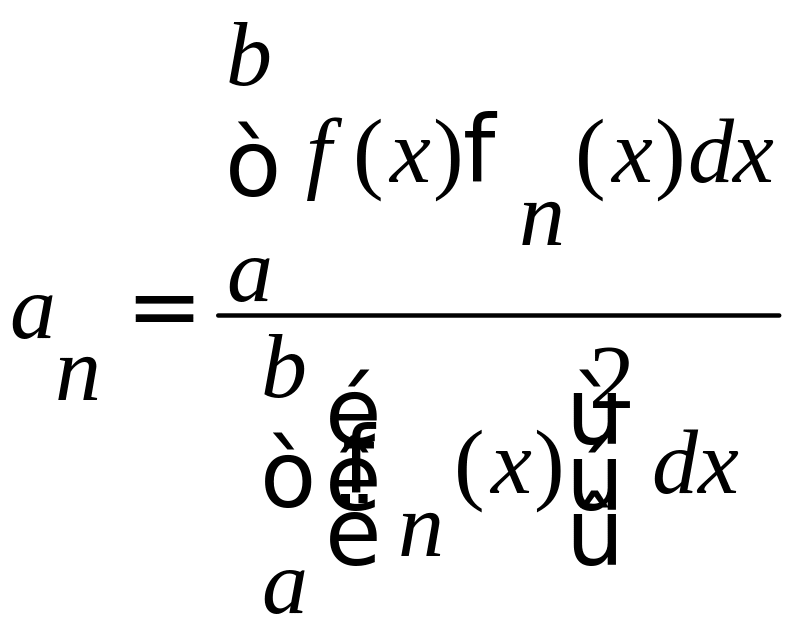где f(x)= - сумма равномерно сходящегося на отрезке [a, b] ряда по ортогональной системе функций. f(x) – любая функция, непрерывная или имеющая конечное число точек разрыва первого рода на отрезке [a, b].

В случае ортонормированной системы функций коэффициенты определяются:

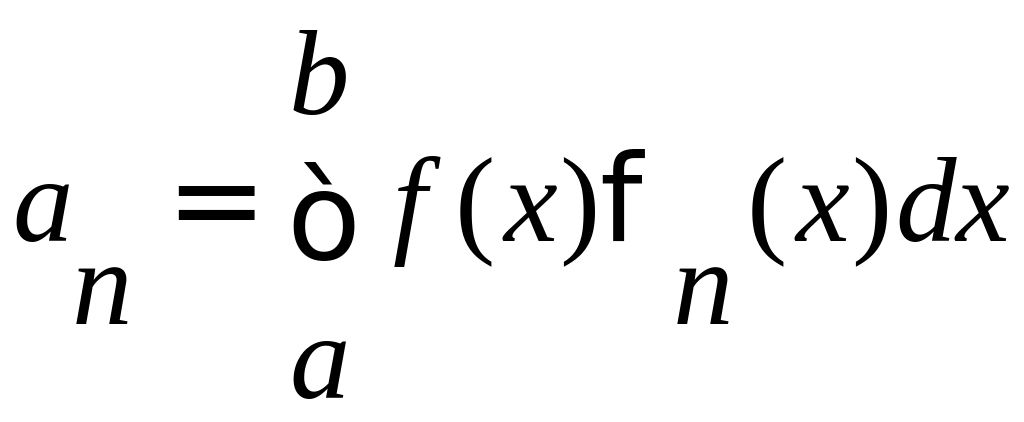
Интеграл Фурье

Пусть функция f(x) на каждом отрезке [-l, l], где l – любое число, кусочно–гладкая или кусочно–монотонная, кроме того, f(x) – абсолютно интегрируемая функция, т.е. сходится несобственный интеграл .

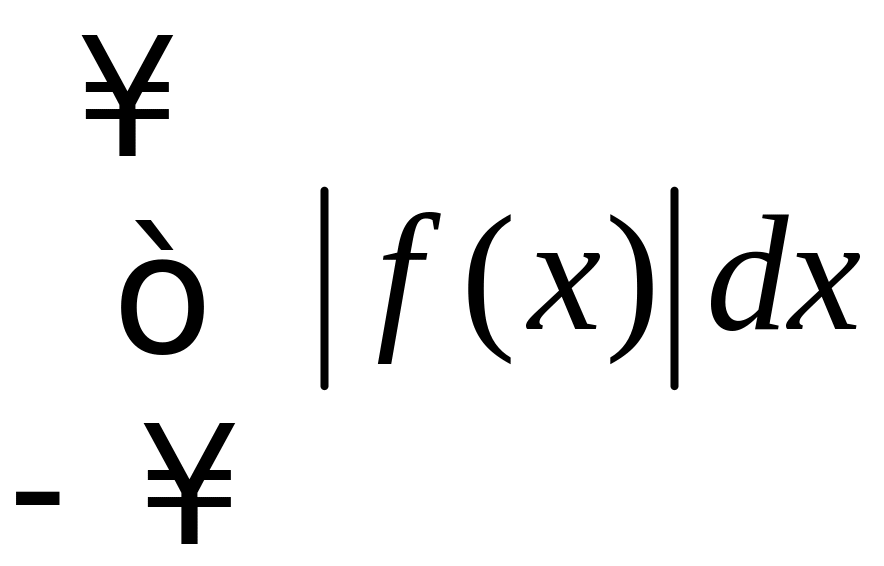Тогда функция f(x) разлагается в ряд Фурье:

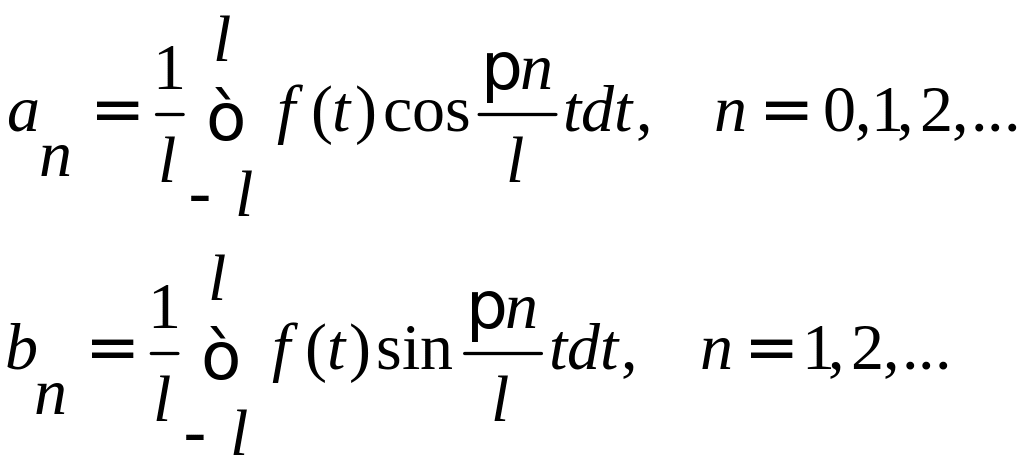
Если подставить коэффициенты в формулу для f(x), получим:

+ .

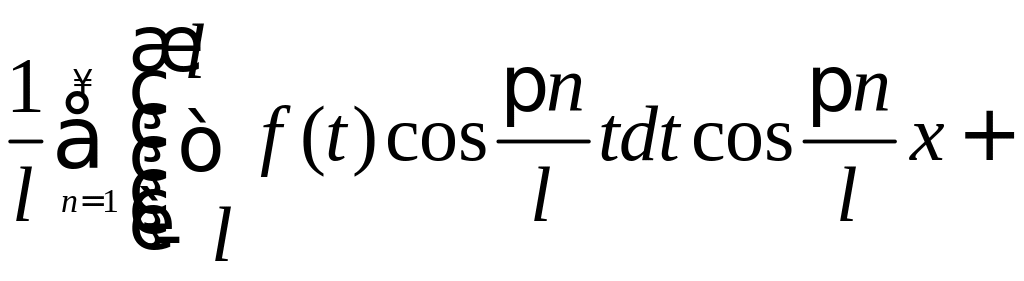
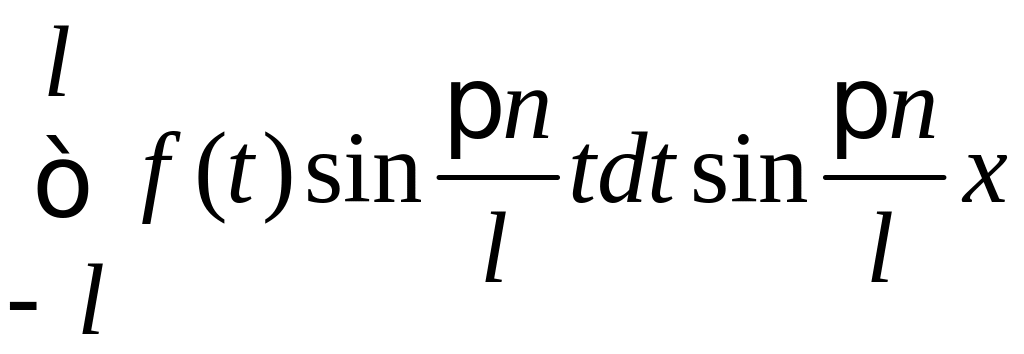
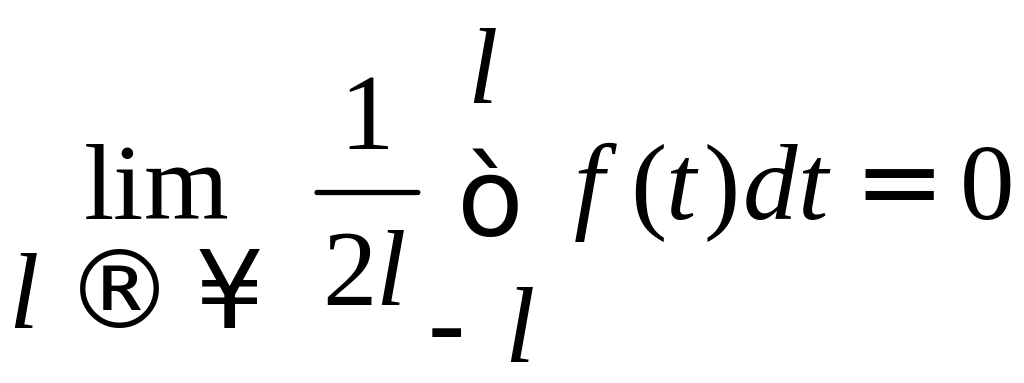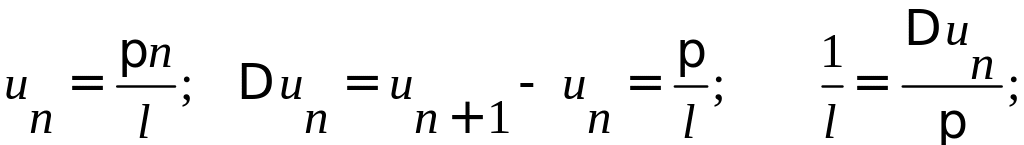Переходя к пределу при l, можно доказать, что и . Обозначим при l u_n 0.