Вычисление интегралов с использованием тригонометрических формул

Вычислим несколько интегралов, которые нам понадобятся в дальнейшем, k и n–натуральные числа

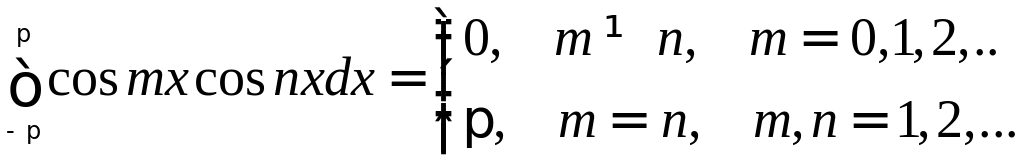
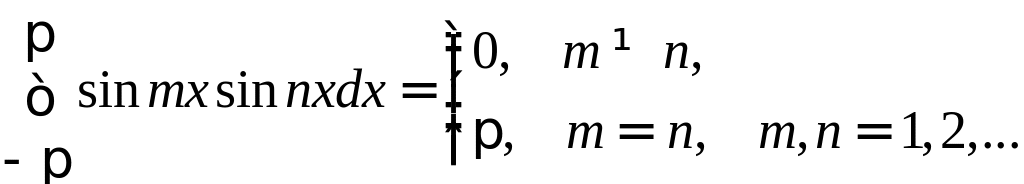
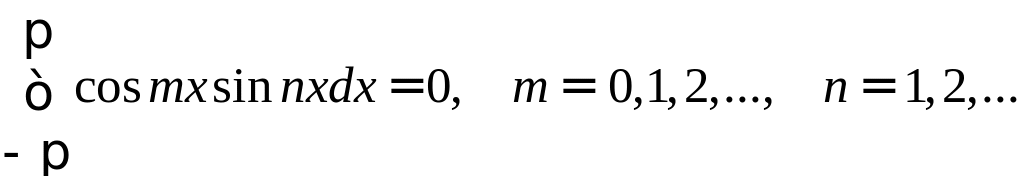
Справедливость этих равенств вытекает из применения к подынтегральному выражению тригонометрических формул.

Так как функция f(x) непрерывна на отрезке [-; ], то существует интеграл

.

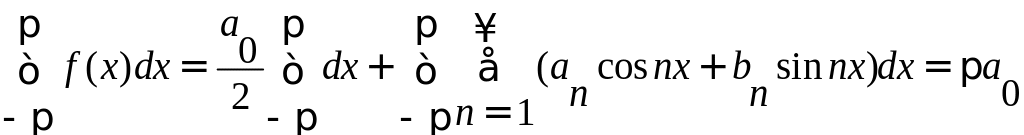Такой результат получается в результате того, что .

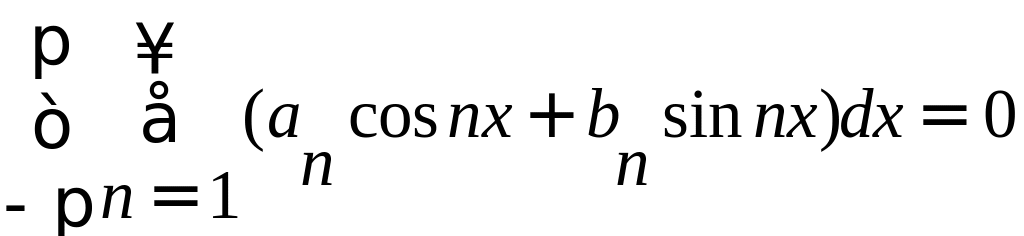Получаем: 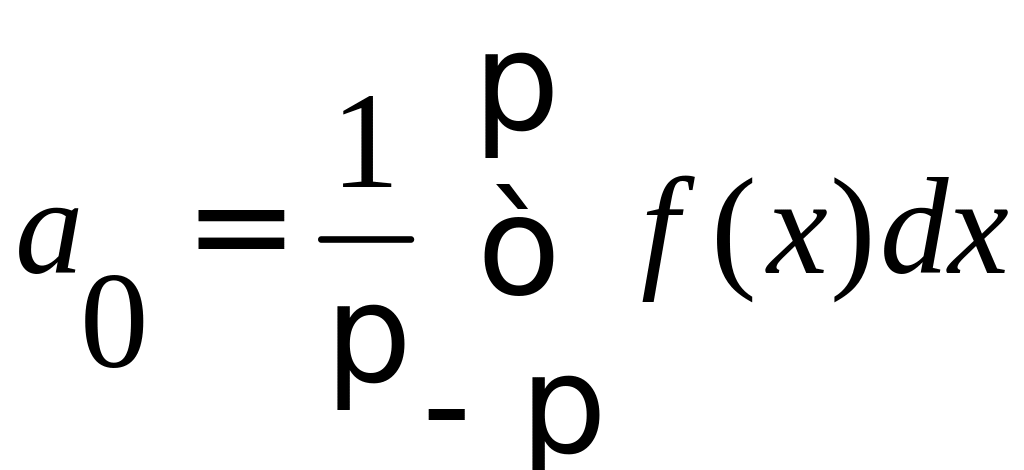. Далее умножаем выражение разложения функции в ряд на cosnx и интегрируем в пределах от - до .

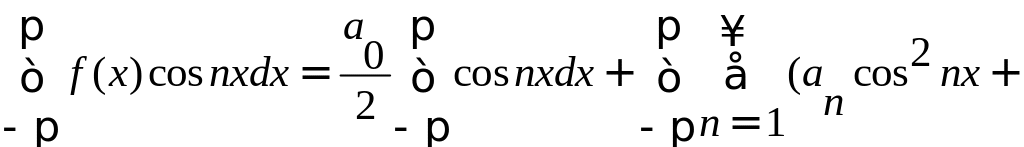
Отсюда получаем:

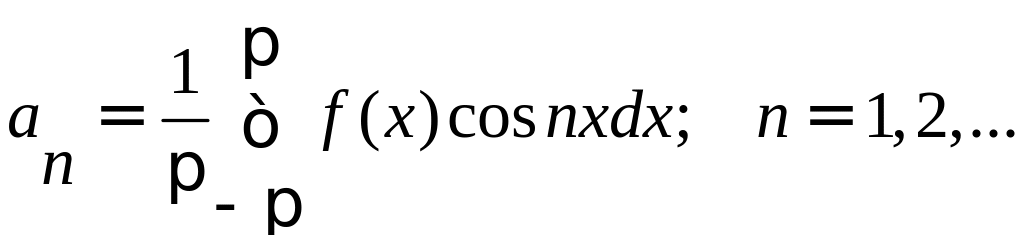
Аналогично умножаем выражение разложения функции в ряд на sinnx и интегрируем в пределах от - до . Получаем:

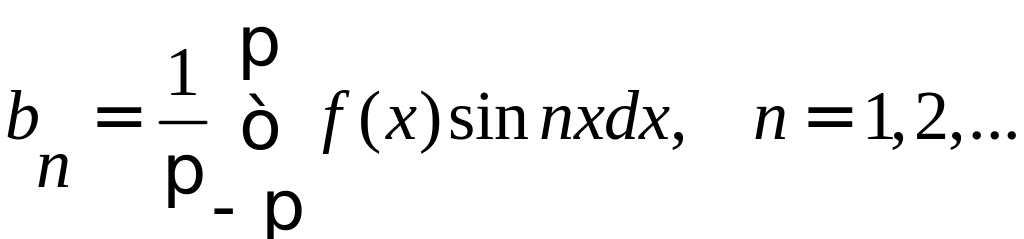
Выражение для коэффициента а₀ является частным случаем для выражения коэффициентов a_n.

Таким образом, если функция f(x) – любая периодическая функция периода 2, непрерывная на отрезке [-; ] или имеющая на этом отрезке конечное число точек разрыва первого рода, то коэффициенты

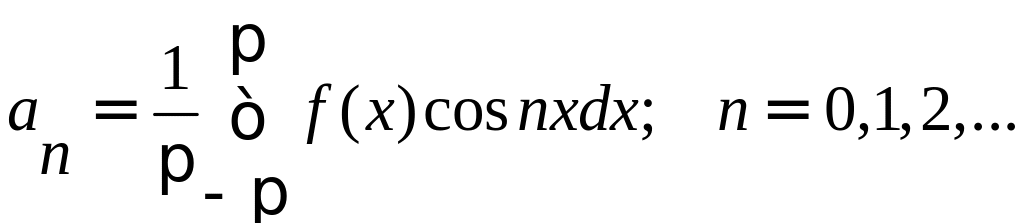
существуют и называются коэффициентами Фурье для функции f(x).

Определение. Рядом Фурье для функции f(x) называется тригонометрический ряд, коэффициенты которого являются коэффициентами Фурье. Если ряд Фурье функции f(x) сходится к ней во всех ее точках непрерывности, то говорят, что функция f(x) разлагается в ряд Фурье.

Теорема (Теорема Дирихле). Если функция f(x) имеет период 2 и на отрезке [-;] непрерывна или имеет конечное число точек разрыва первого рода, и отрезок [-;] можно разбить на конечное число отрезков так, что внутри каждого из них функция f(x) монотонна, то ряд Фурье для функции f(x) сходится при всех значениях х, причем в точках непрерывности функции f(x) его сумма равна f(x), а в точках разрыва его сумма равна 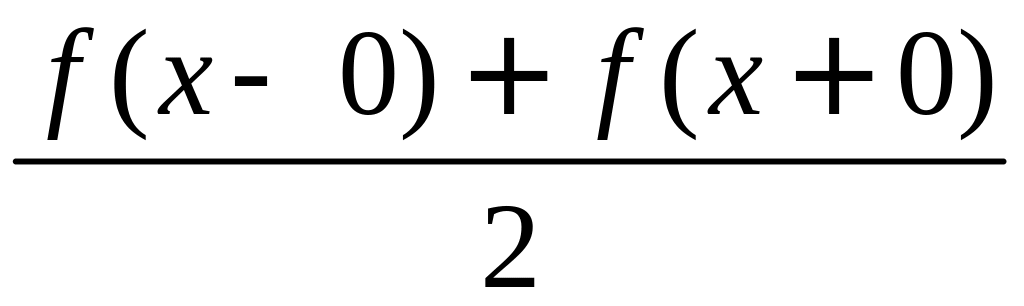, т.е. среднему арифметическому предельных значений слева и справа. При этом ряд Фурье функции f(x) сходится равномерно на любом отрезке, который принадлежит интервалу непрерывности функции f(x).

Пример: Разложить в ряд Фурье функцию с периодом

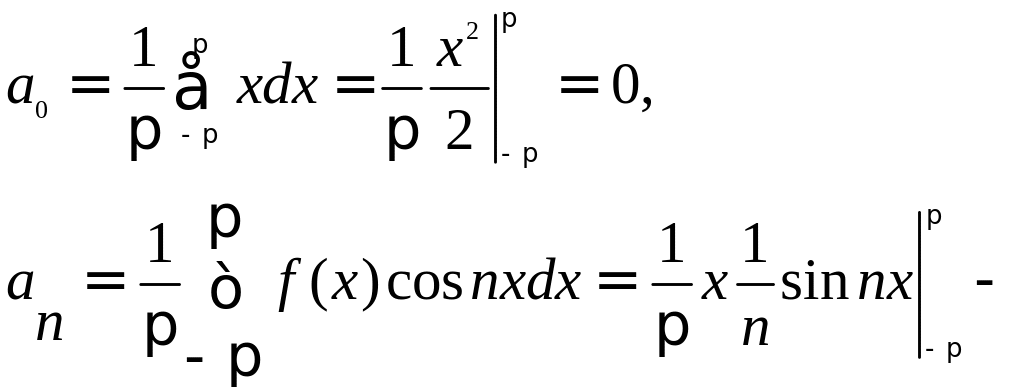
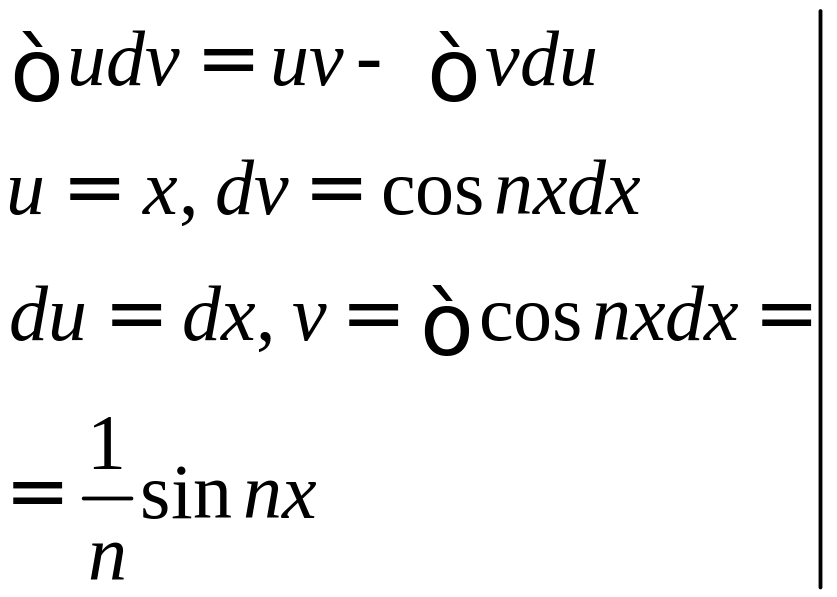
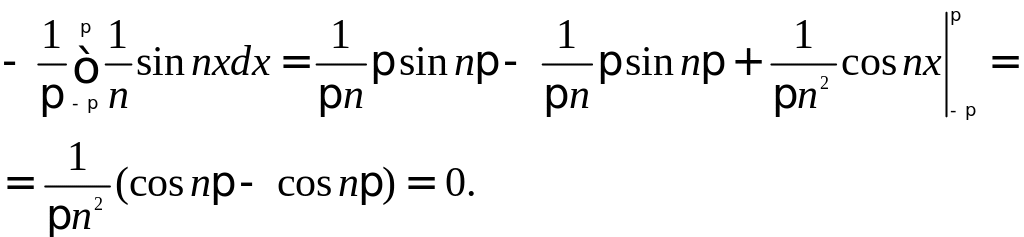
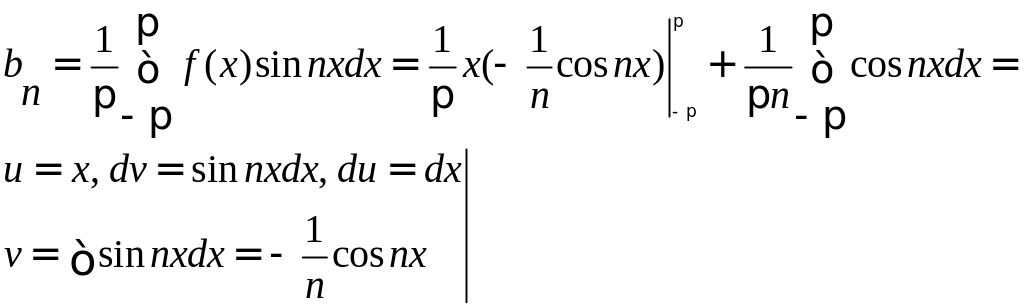
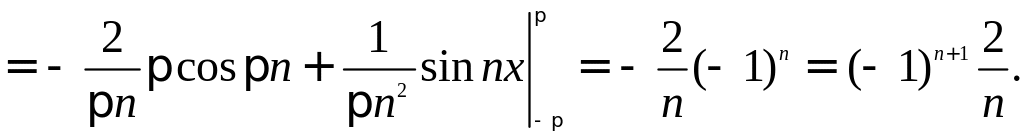
Получаем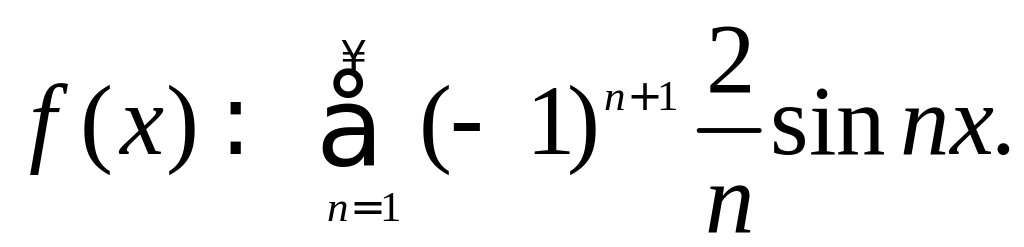

Замечание: Нетрудно показать, что если функция f(x) имеет период , то

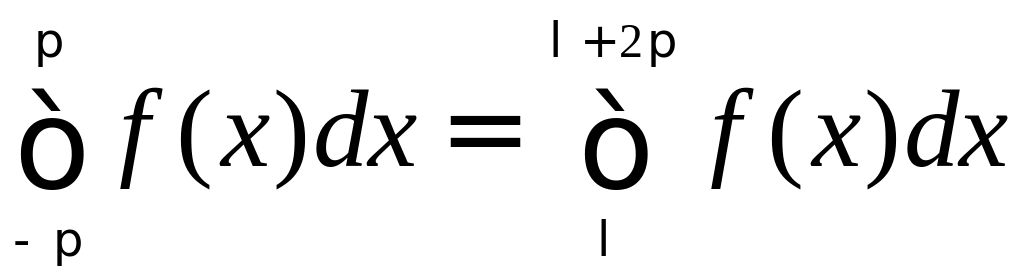, где l – любое число.

Функция f(x), для которой выполняются условия теоремы Дирихле называется кусочно–монотонной на отрезке [-;].

Ряд Фурье для четных и нечетных функций

Отметим следующие свойства четных и нечетных функций:

1)

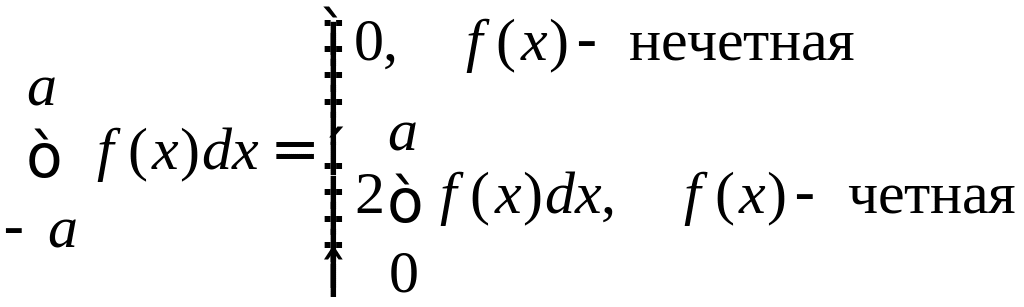
2) Произведение двух четных и нечетных функций является четной функцией.

3) Произведение четной и нечетной функций – нечетная функция.

Справедливость этих свойств может быть легко доказана исходя из определения четности и нечетности функций.

Если f(x) – четная периодическая функция с периодом 2, удовлетворяющая условиям разложимости в ряд Фурье, то можно записать:

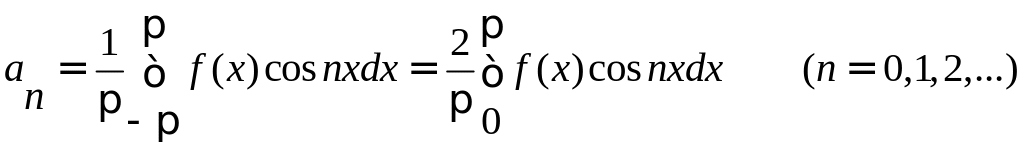
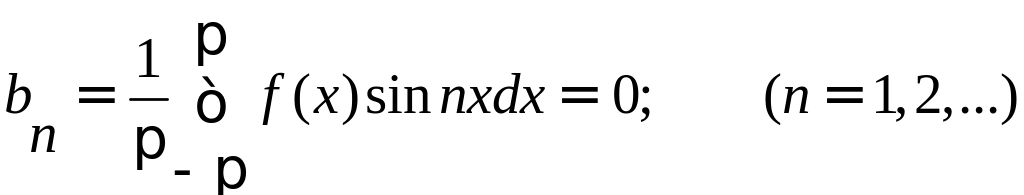
Таким образом, для четной функции ряд Фурье записывается:

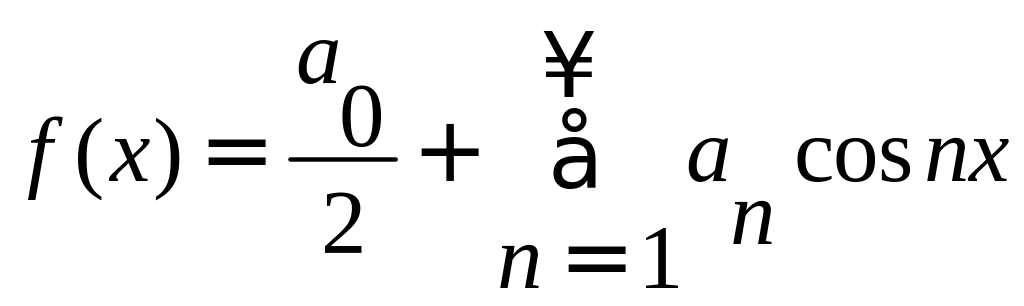
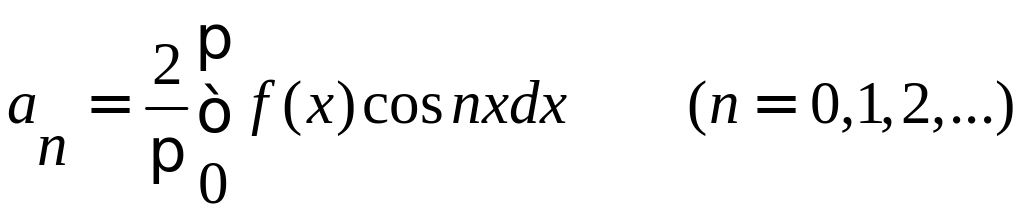
Аналогично получаем разложение в ряд Фурье для нечетной функции:

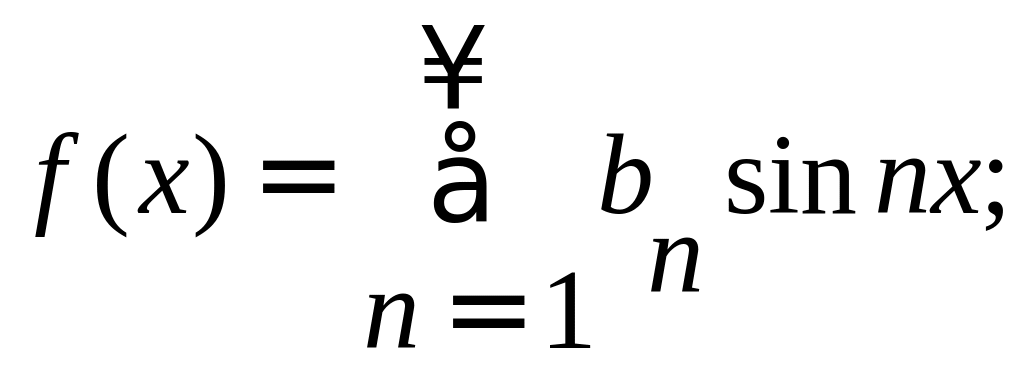
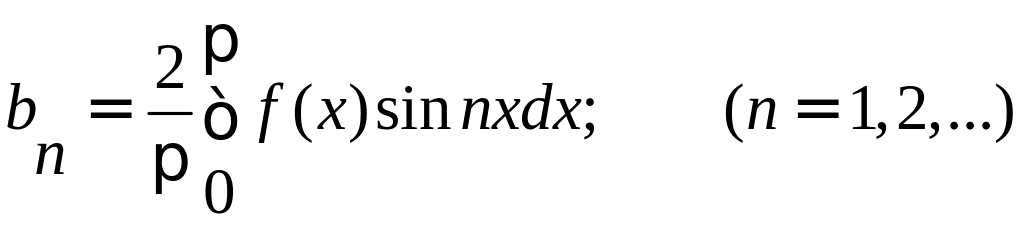
Пример. Разложить в ряд Фурье периодическую функцию с периодом T = 2 на отрезке [-; ].

Заданная функция является нечетной, следовательно, коэффициенты Фурье ищем в виде:

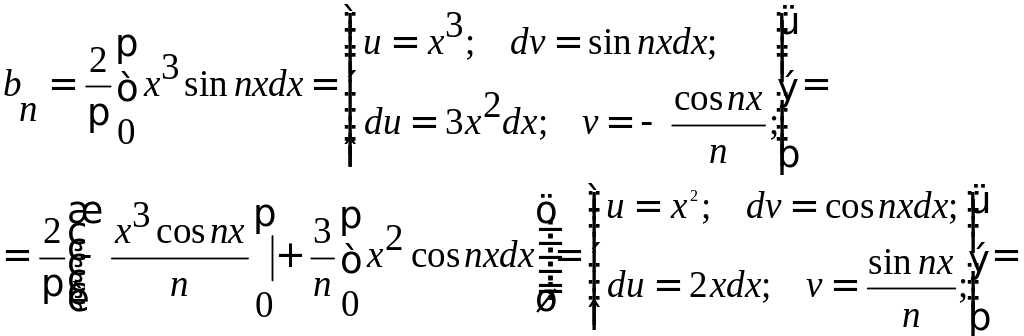
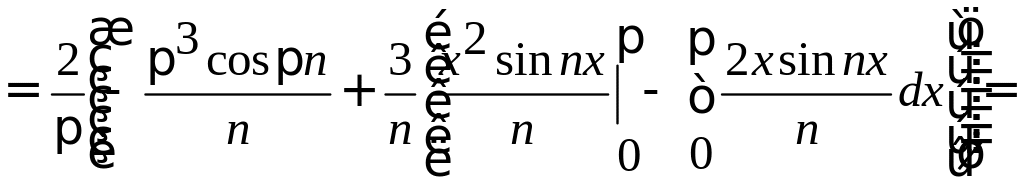
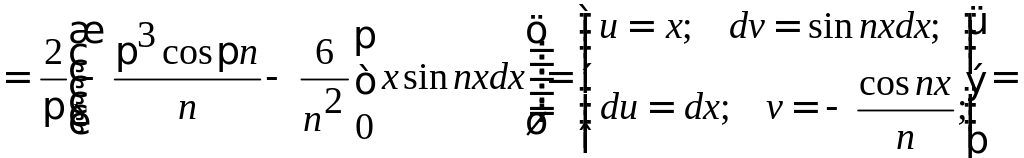
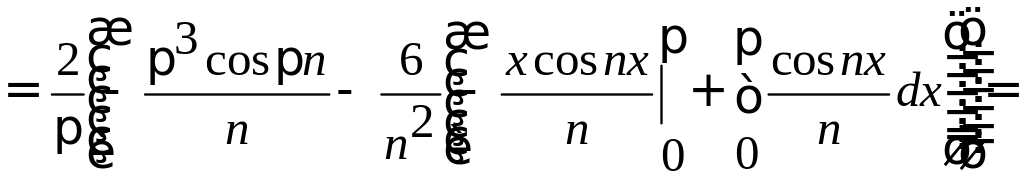
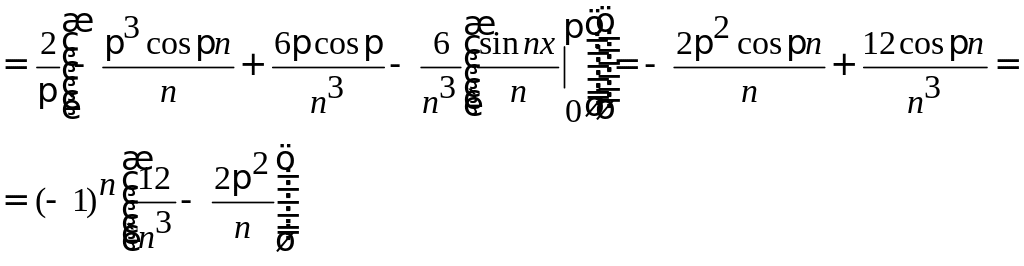
Получаем:

.

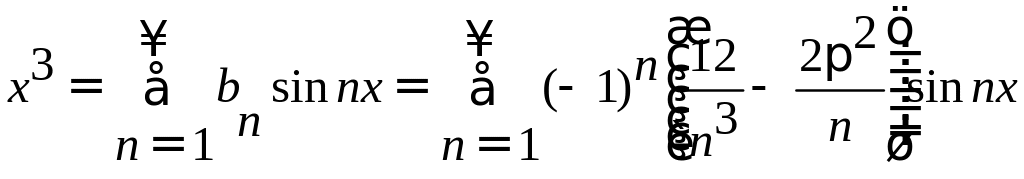Построим графики (рисунок 1) заданной функции и ее разложения в ряд Фурье, ограничившись первыми четырьмя членами ряда.

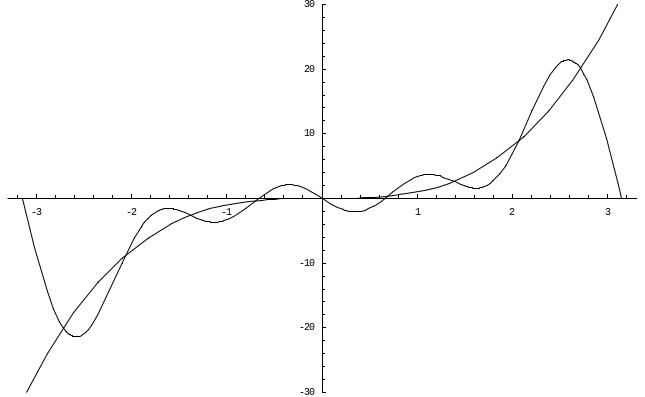
Рисунок 1

Пример: Разложить в ряд Фурье функцию с периодом . Данная функция четная, поэтому

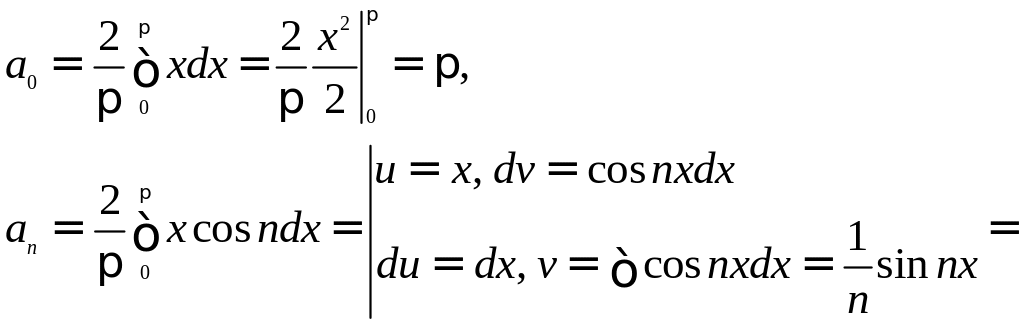
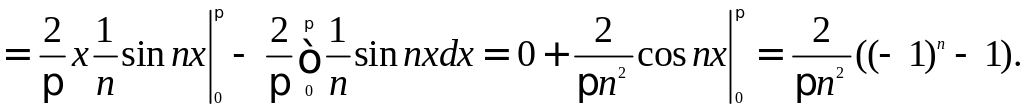
Заметим, что

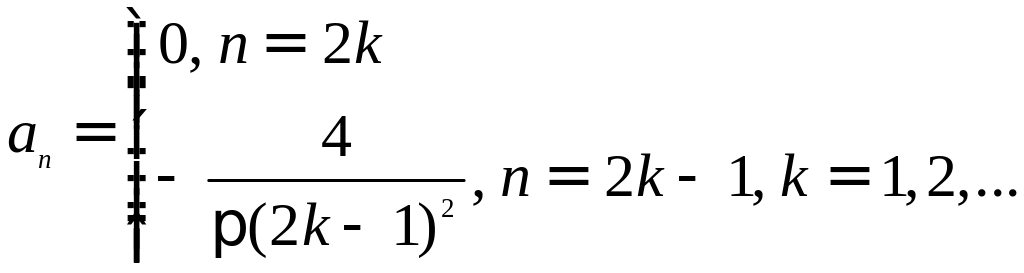
Получим ряд Фурье:

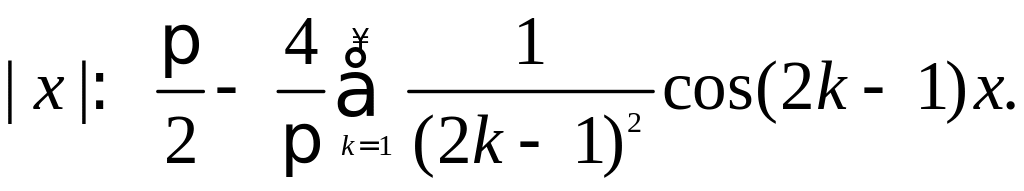
Разложение в ряд Фурье непериодических функций

Если функция задана на всей числовой оси и непериодическая, то её нельзя разложить в ряд Фурье, так как сумма тригонометрического ряда является периодической функцией.

Рассмотрим непериодическую непрерывную функцию на промежутке и построим ряд Фурье, который имел бы её своей суммой в этом интервале. Для этого рассмотрим вспомогательную функцию с периодом такую, что при . Разложив в ряд Фурье функцию , мы получили тем самым разложение на .

Если функция задана только в промежутке , то для разложения её в ряд Фурье на этом промежутке, нужно сначала продолжить её каким–то образом на промежуток , а затем продолжить периодически с периодом на всю числовую ось. Чаще всего на промежуток функцию продолжают чётным или нечётным образом.

Пример. Разложить функцию заданную на [0; 1] в ряд по синусам. Продолжим данную функцию в интервал (-1, 0) нечётным образом, а затем продолжим периодически с периодом 2e=2 на всю числовую ось. Тогда

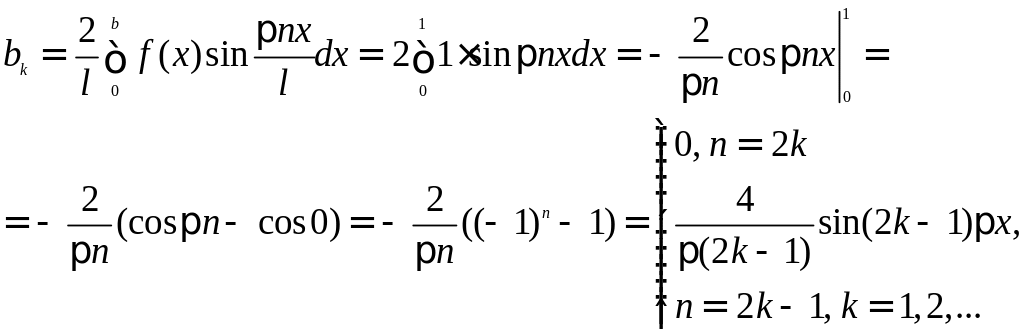
Получаем ряд Фурье: .

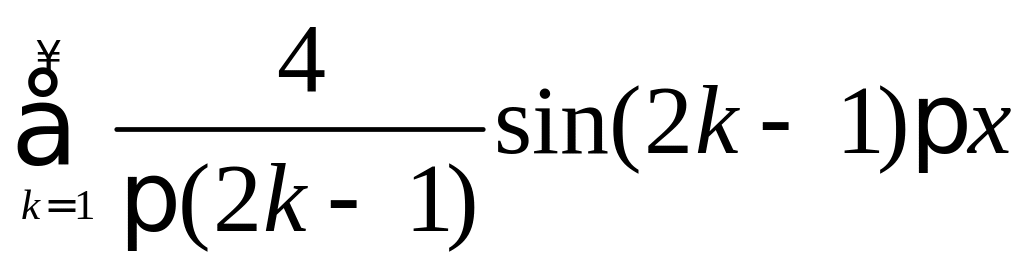Ряды Фурье для функций любого периода

Ряд Фурье для функции f(x) периода Т = 2l, непрерывной или имеющей конечное число точек разрыва первого рода на отрезке

[-l, l] имеет вид:

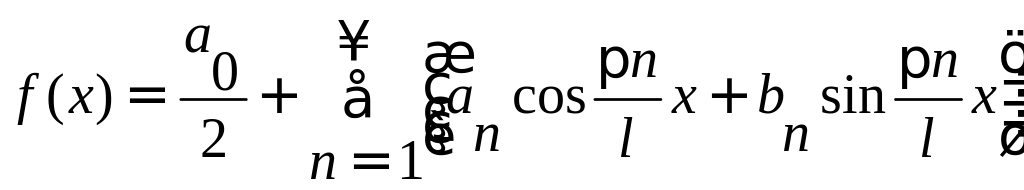
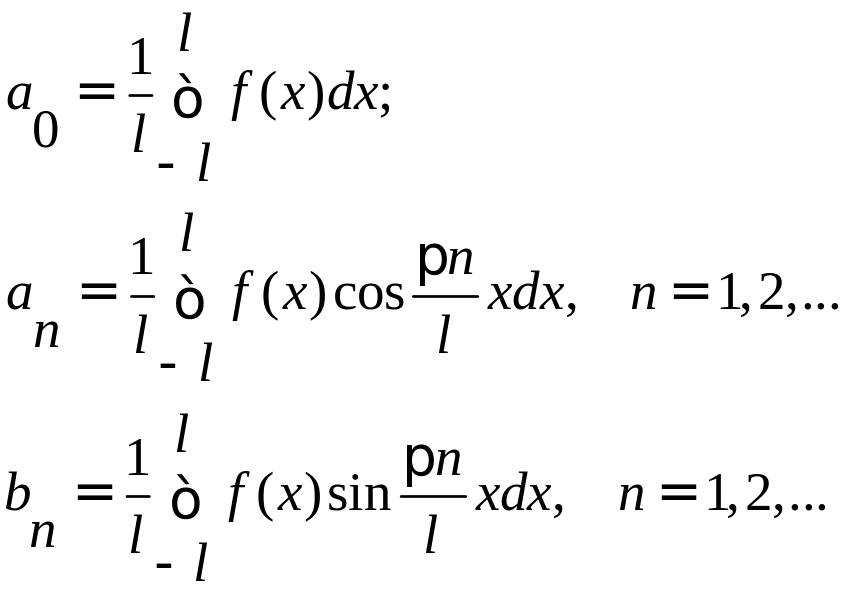
Для четной функции произвольного периода разложение в ряд Фурье имеет вид:

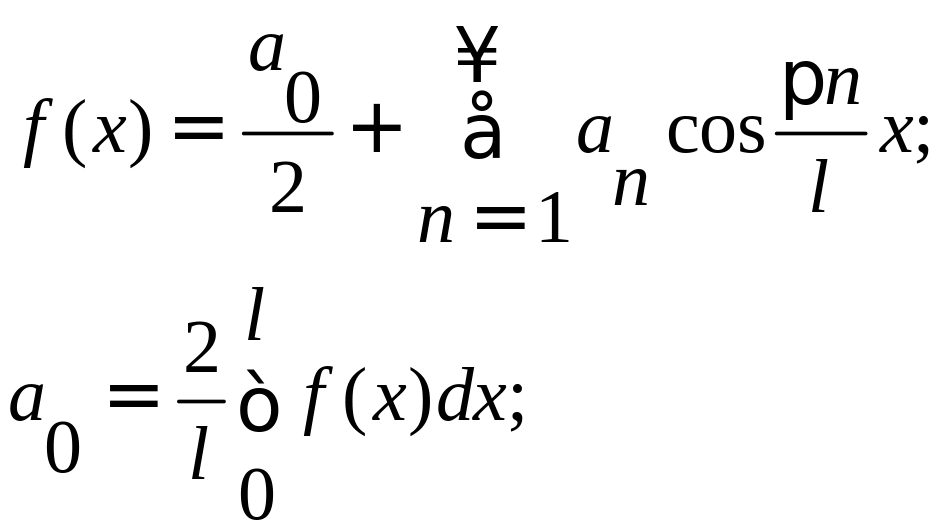
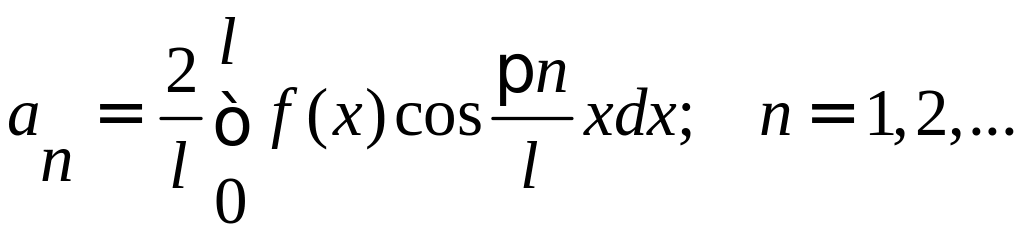
Для нечетной функции:

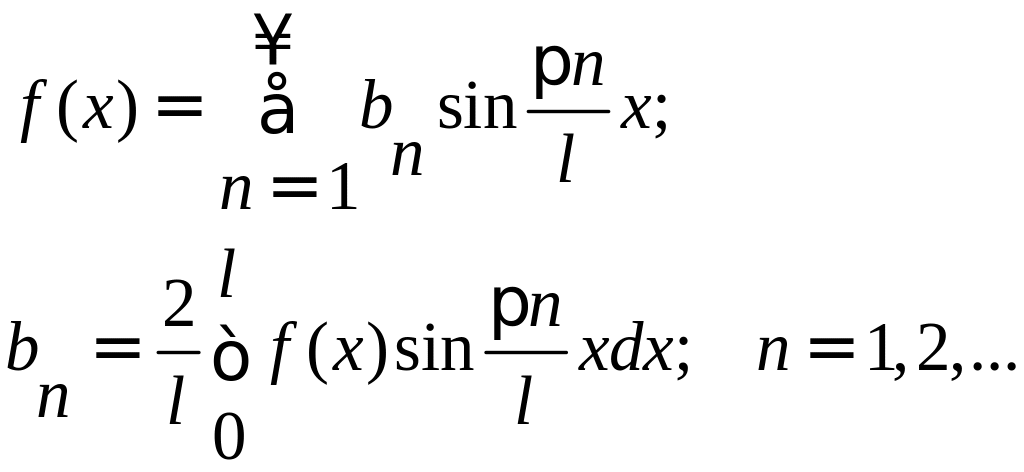
Ряд Фурье по ортогональной системе функций

Определение. Функции (х) и (х), определенные на отрезке [a, b], называются ортогональными на этом отрезке, если

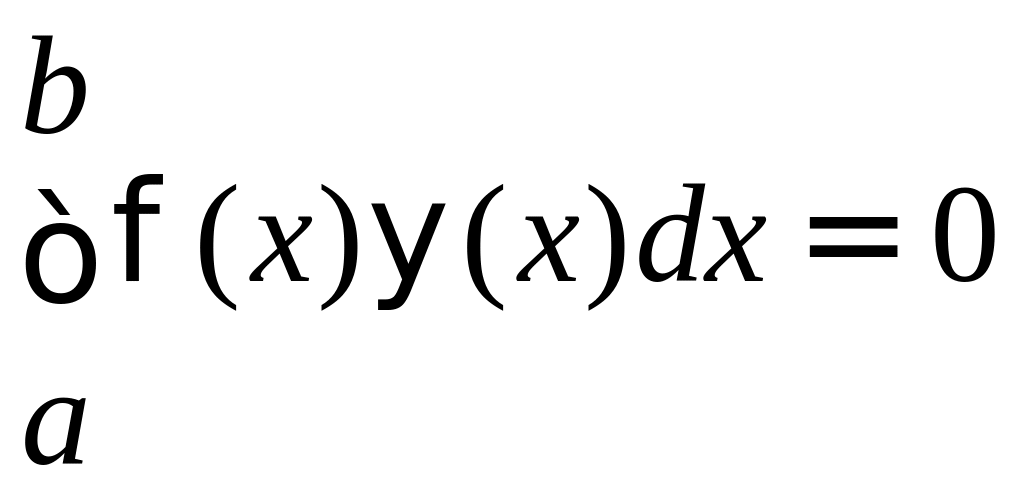
Определение. Последовательность функций ₁(x), ₂(x), …, _n(x), непрерывных на отрезке [a, b], называется ортогональной системой функций на этом отрезке, если все функции попарно ортогональны.

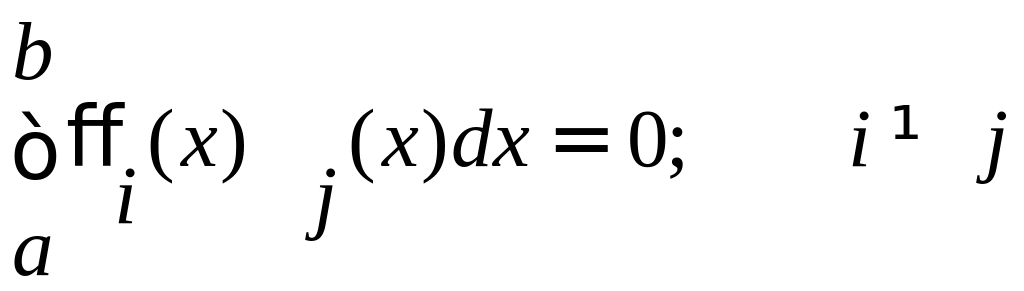
Отметим, что ортогональность функций не подразумевает перпендикулярности графиков этих функций.

Определение. Система функций называется ортогональной и нормированной (ортонормированной), если

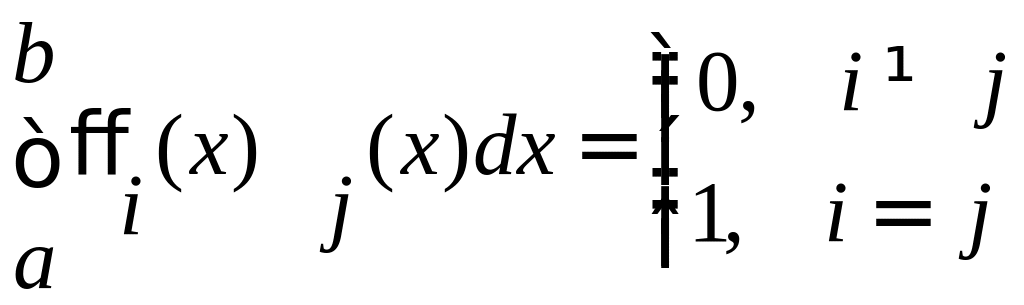
Определение. Рядом Фурье по ортогональной системе функций ₁(x), ₂(x), …,_n(x) называется ряд вида: 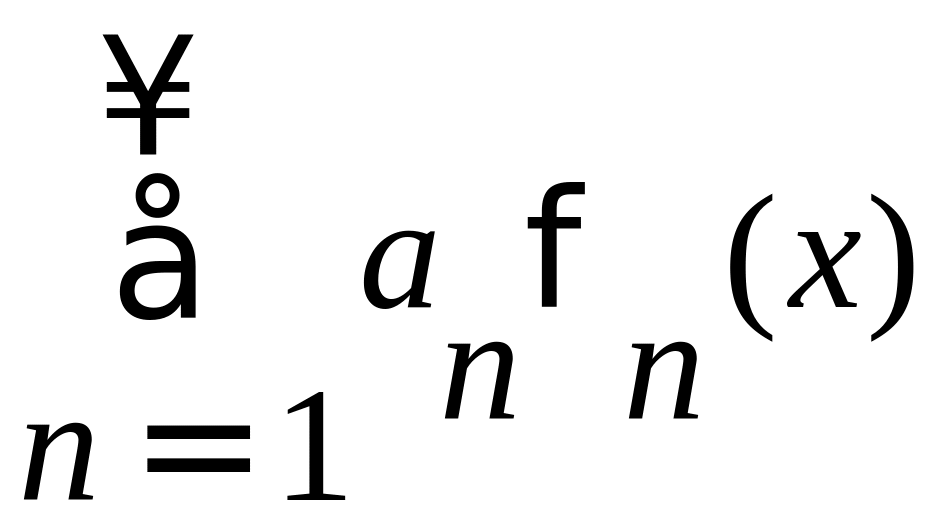коэффициенты которого определяются по формуле:

,

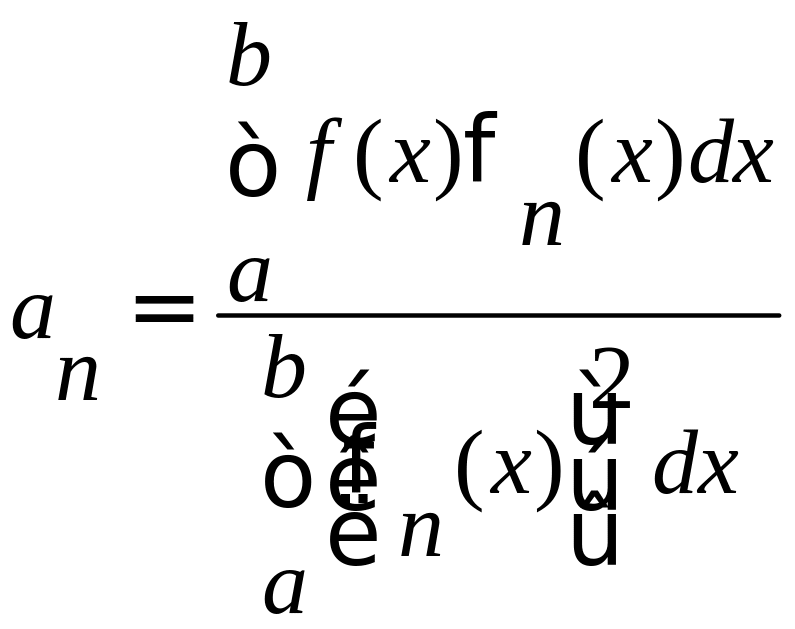где 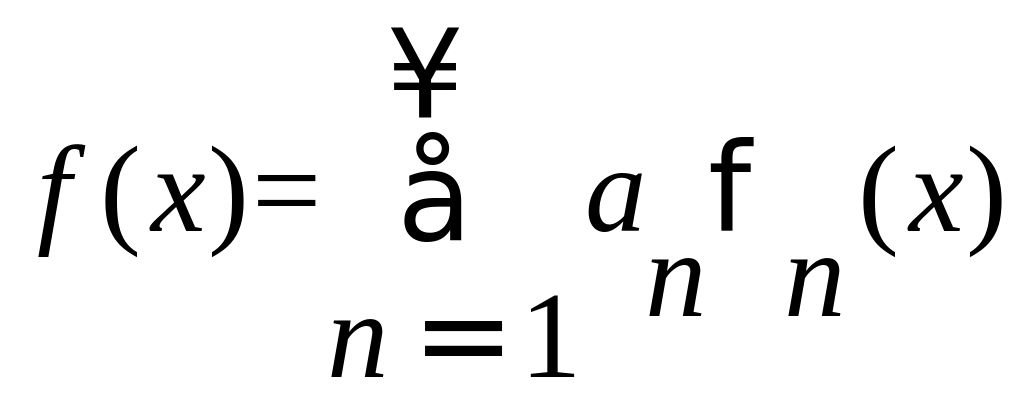- сумма равномерно сходящегося на отрезке [a, b] ряда по ортогональной системе функций. f(x) – любая функция, непрерывная или имеющая конечное число точек разрыва первого рода на отрезке [a, b].

В случае ортонормированной системы функций коэффициенты определяются:

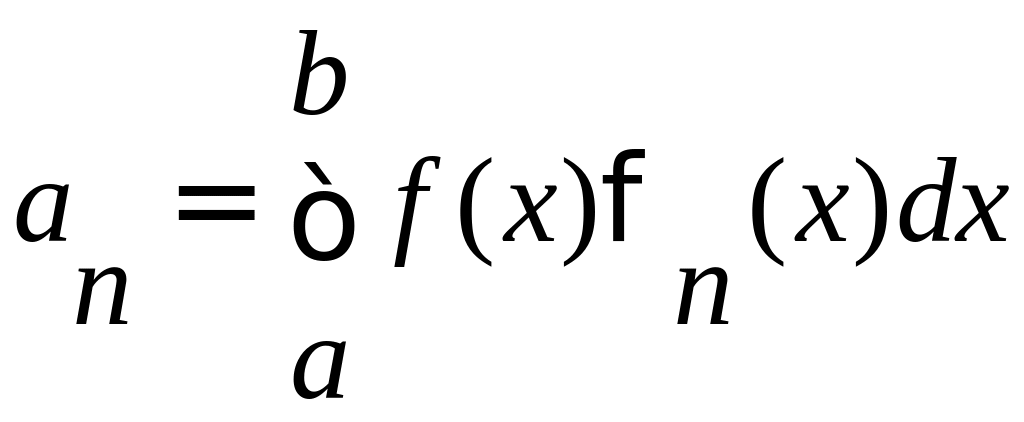
Интеграл Фурье

Пусть функция f(x) на каждом отрезке [-l, l], где l – любое число, кусочно–гладкая или кусочно–монотонная, кроме того, f(x) – абсолютно интегрируемая функция, т.е. сходится несобственный интеграл .

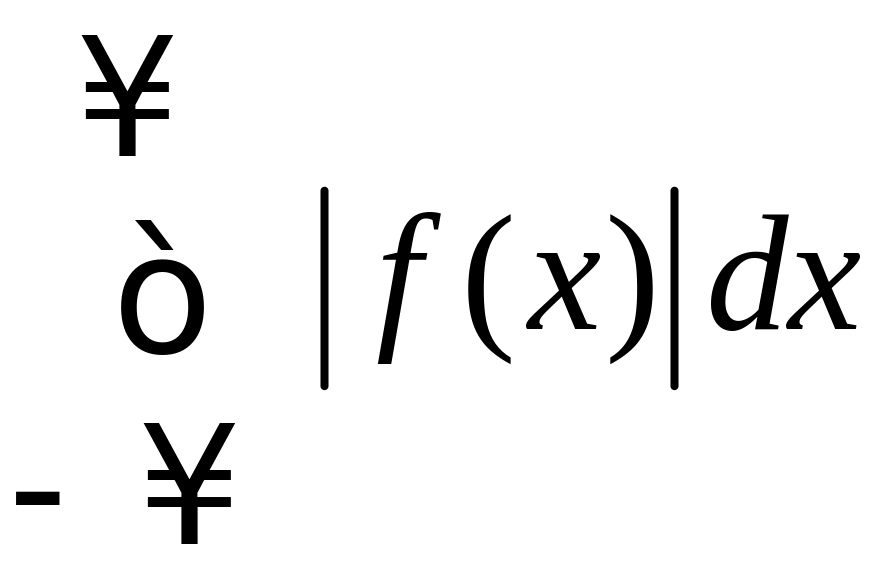Тогда функция f(x) разлагается в ряд Фурье:

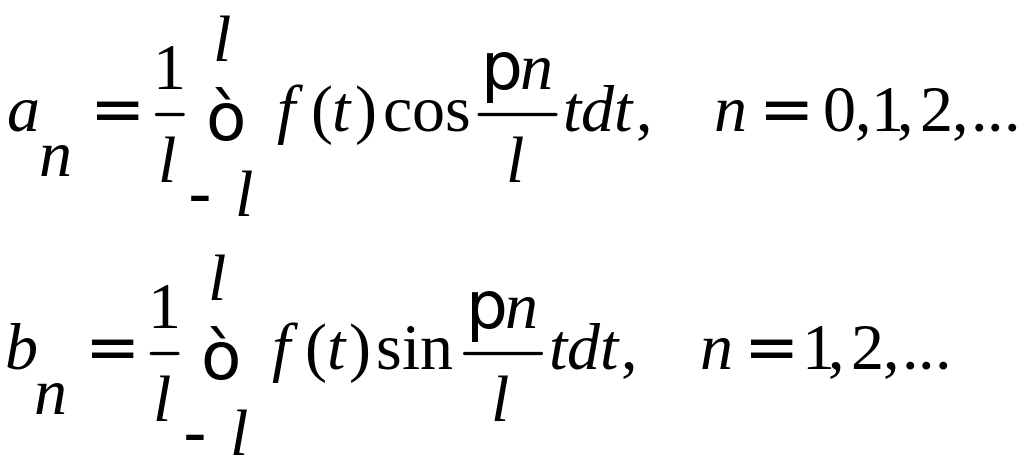
Если подставить коэффициенты в формулу для f(x), получим:

+ .

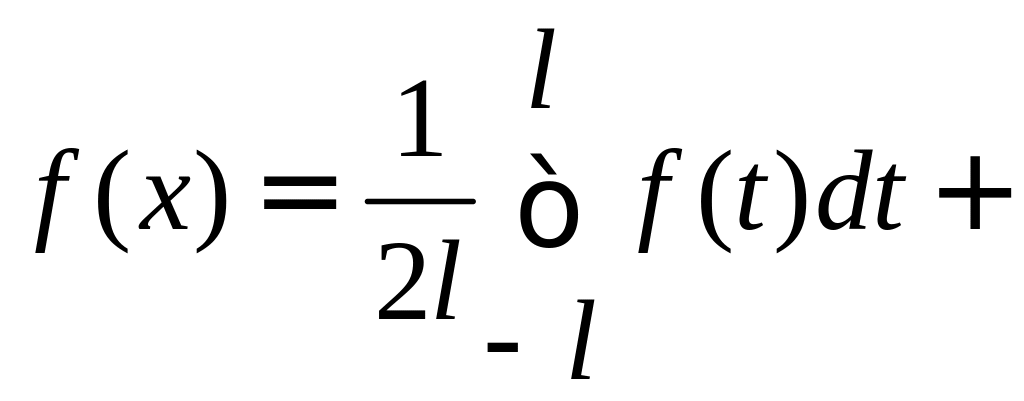
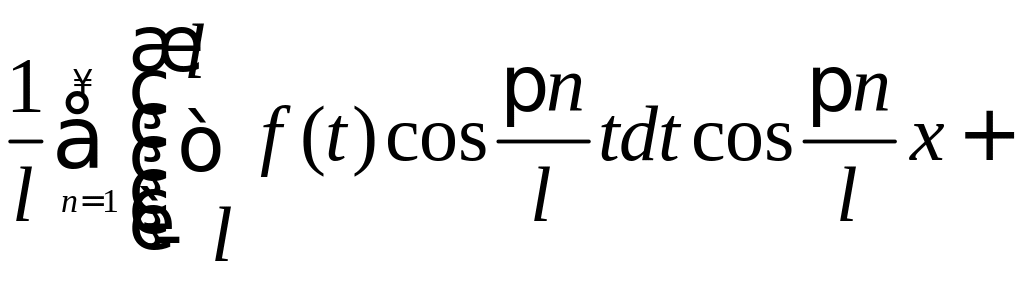
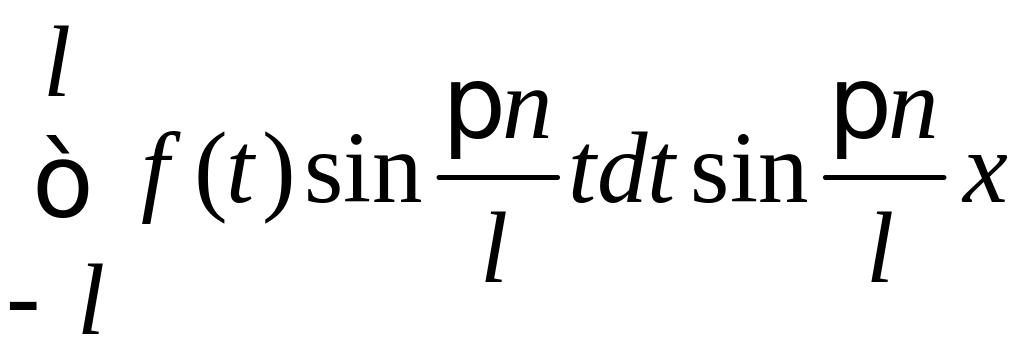
Переходя к пределу при l, можно доказать, что 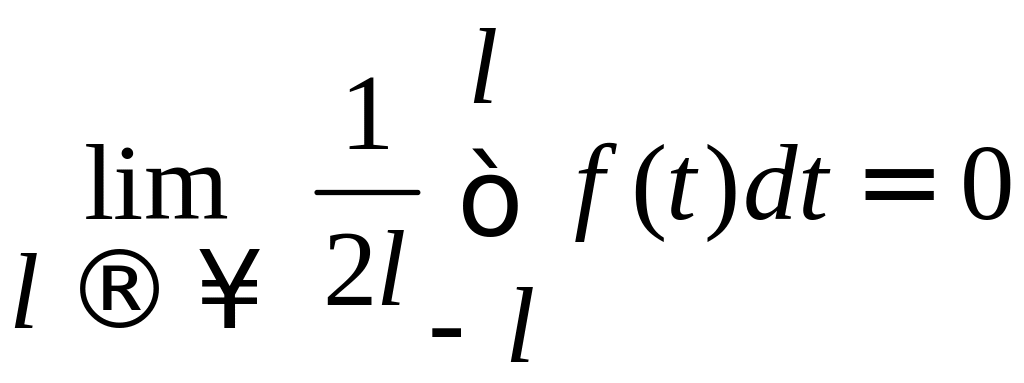и 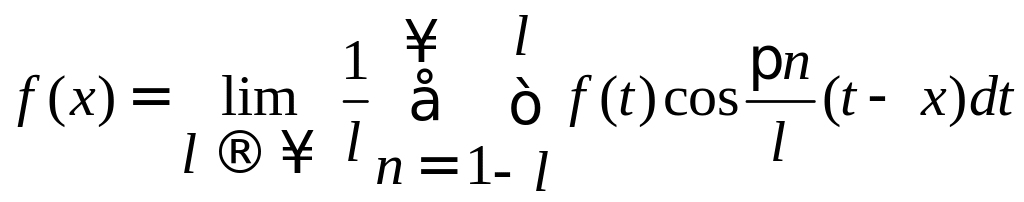. Обозначим 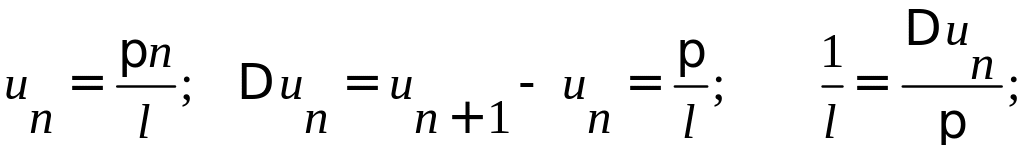при l u_n 0.

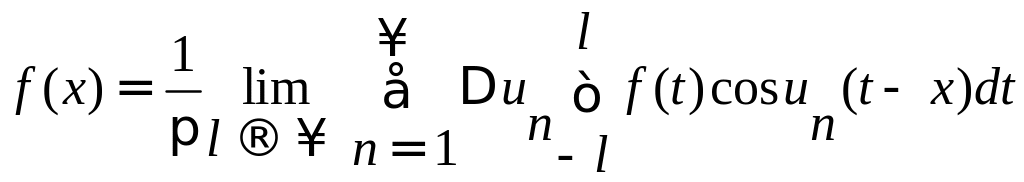
Можно доказать, что предел суммы, стоящий в правой части равенства, равен интегралу

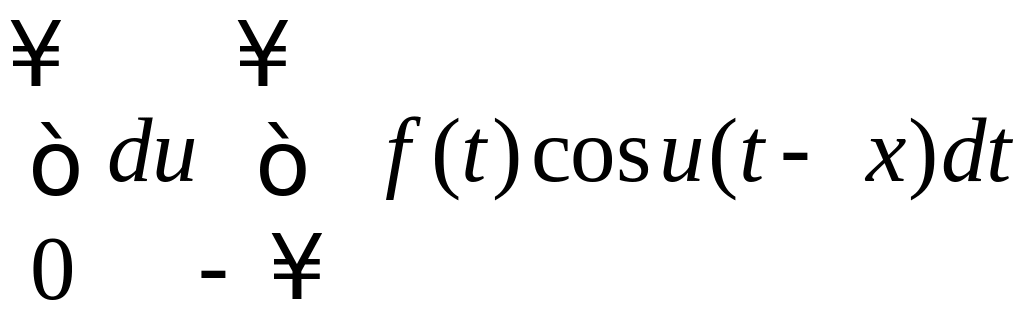
Тогда - двойной интеграл Фурье.

Окончательно получаем:

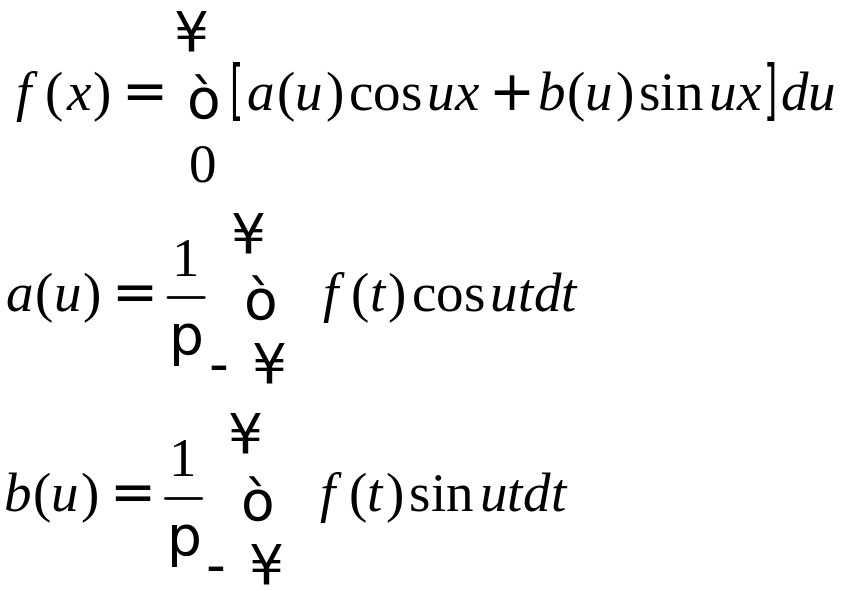
- представление функции f(x) интегралом Фурье.

Двойной интеграл Фурье для функции f(x) можно представить в комплексной форме:

.

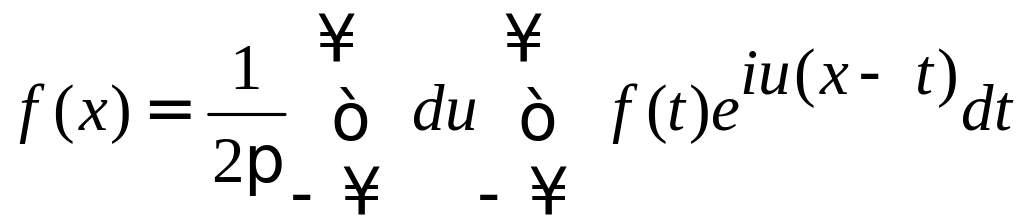Преобразование Фурье

Определение. Если f(x) – любая абсолютно интегрируемая на всей числовой оси функция, непрерывная или имеющая конечное число точек разрыва первого рода на каждом отрезке, то функция

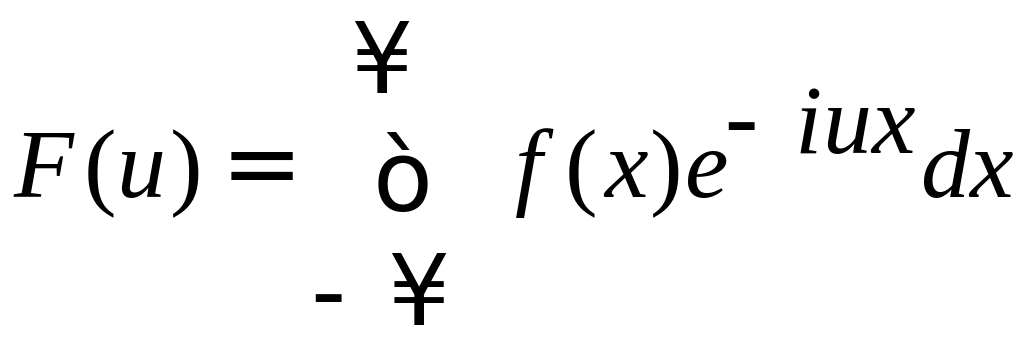
называется преобразованием Фурье функции f(x).

Функция F(u) называется также спектральной характеристикой функции f(x).

Если f(x) – функция, представимая интегралом Фурье, то можно записать:

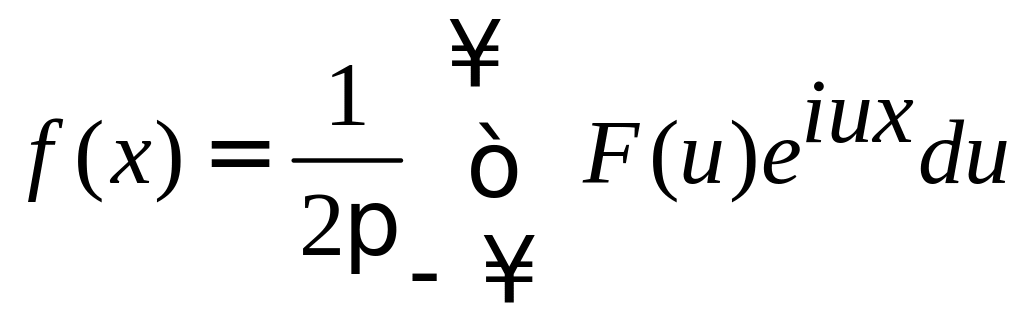
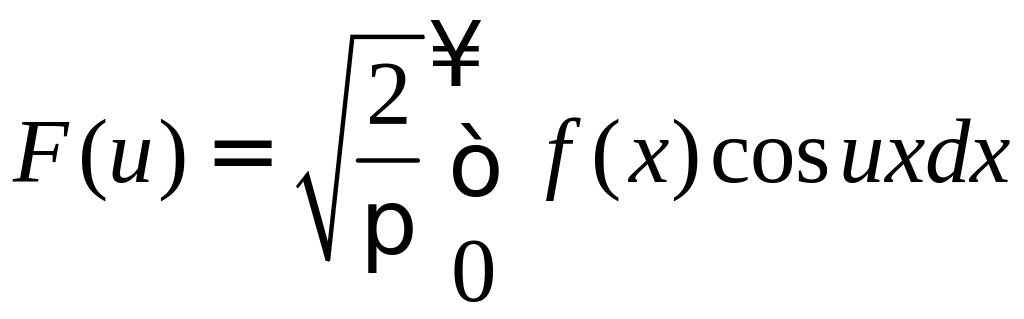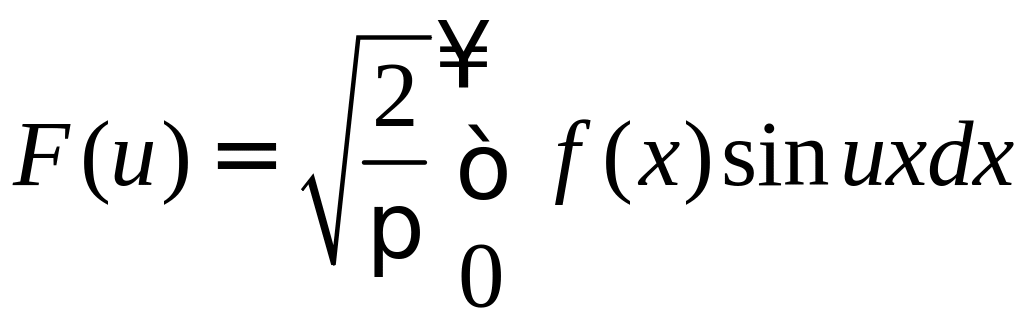Это равенство называется обратным преобразованием Фурье. Интегралы и называются соответственно косинус - преобразование Фурье и синус – преобразование Фурье.

Косинус – преобразование Фурье будет преобразованием Фурье для четных функций, синус – преобразование – для нечетных.

Преобразование Фурье применяется в функциональном анализе, гармоническом анализе, операционном исчислении, теории линейных систем и др.

_{Примеры разложения функций в ряды Фурье}

_{Пример. Периодическая функция ƒ(x) с периодом 2π определяется следующим образом: ƒ(x)=х , -π<x≤π (рисунок 2).}

_{Эта функция – кусочно-монотонная и ограниченная. Следовательно, её можно разложить в ряд Фурье.}

y

x

_{Рисунок 2}

_{Находим:}

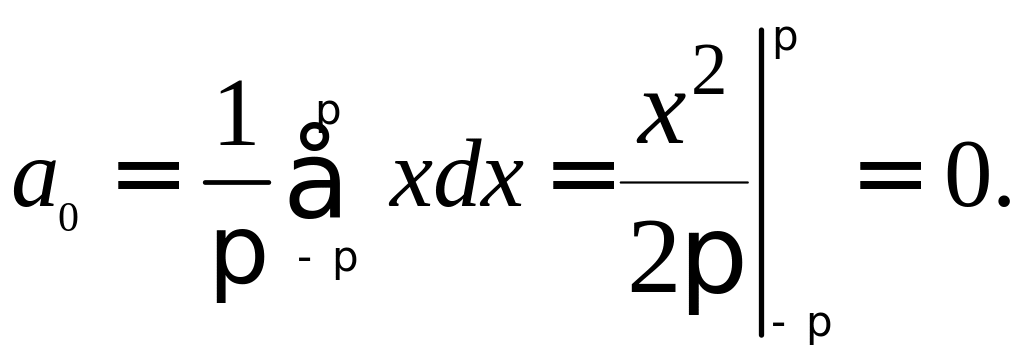
_{Интегрируя по частям, получим:}

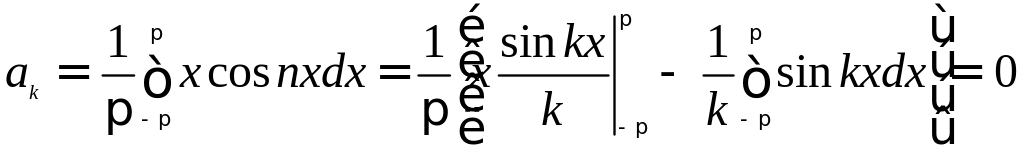
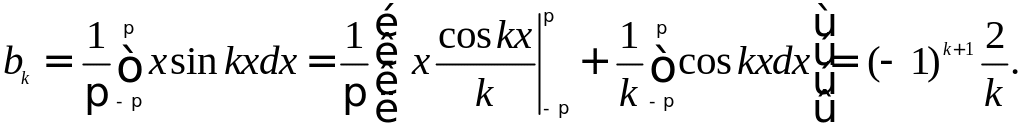
_{Таким образом, получаем ряд:}

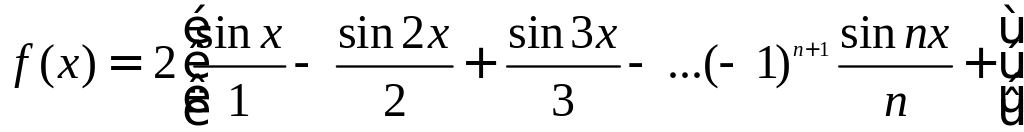
_{Это равенство имеет место во всех точках, кроме точек разрыва. В каждой точке разрыва сумма ряда равна среднему арифметическому ее пределов справа и слева, т. е. нулю.}

_{Пример. Периодическая функция ƒ(x) с периодом 2π определена следующим образом:}

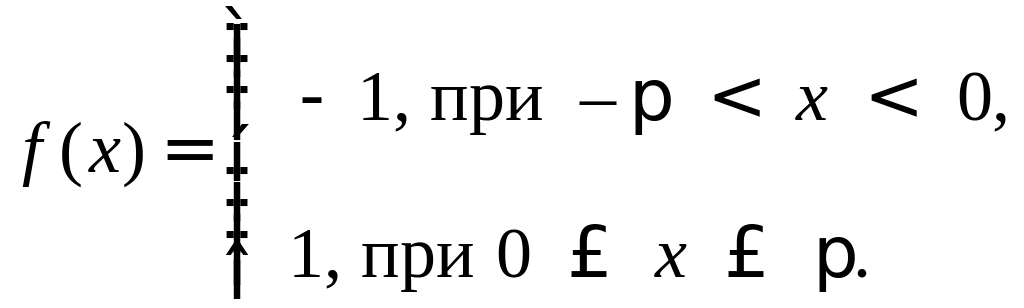
_{Эта функция кусочно-монотонная и ограничена на отрезке [-π, π]. Вычислим ее коэффициенты Фурье:}

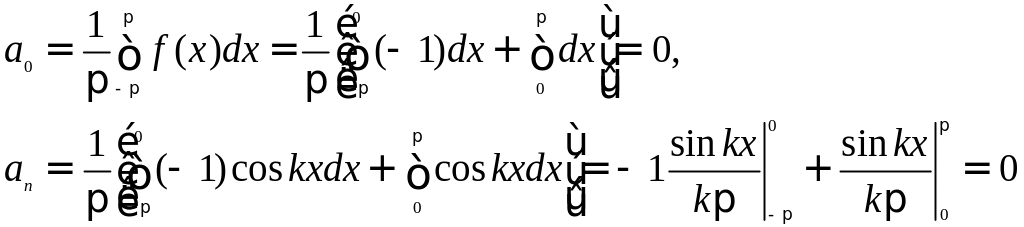
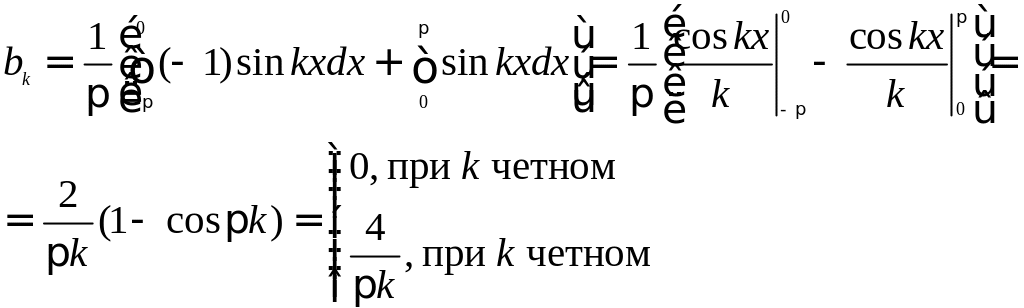
_{Следовательно, для рассматриваемой функции ряд Фурье имеет вид:}

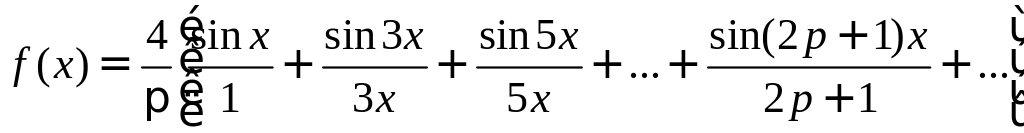
_{Это равенство справедливо во всех точках, кроме точек разрыва.}

_{Замечание о разложении периодической функции в ряд Фурье}

_{Отметим следующее свойство периодической функции ψ(x) с периодом 2π: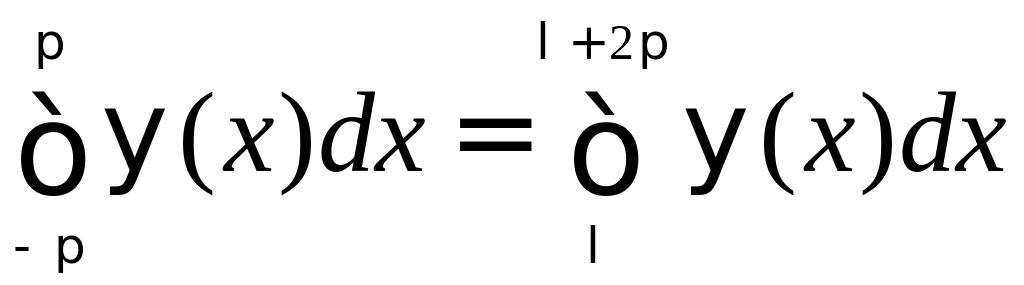} , _{каково бы ни было число λ.}

_{Действительно, так как ψ(ξ - 2π) = ψ (ξ) , то, полагая x = ξ - π, можем написать при любых c и d:}

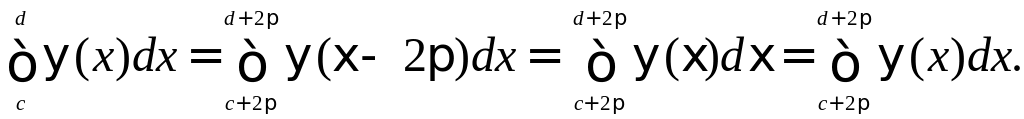
_{В частности, принимая с=-π, d=λ, получим:}

,

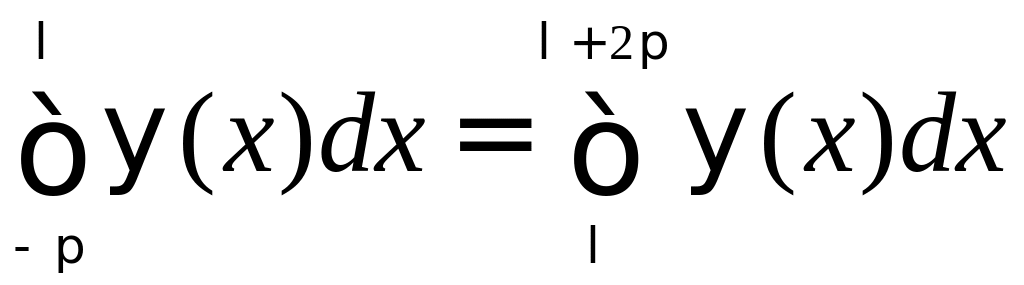_{поэтому}

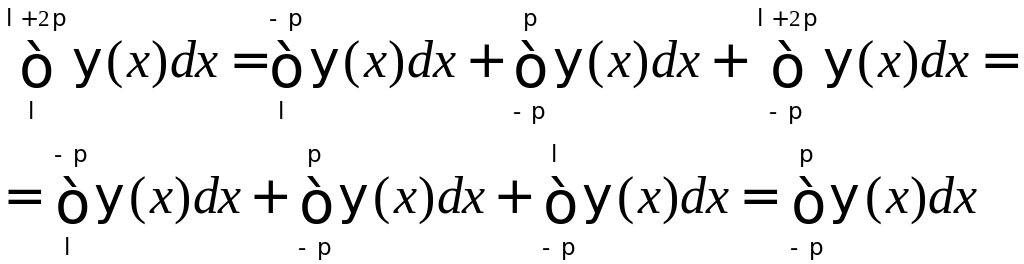
_{Указанное свойство означает, что интеграл от периодической функции ψ(x) по любому отрезку, длина которого равна периоду, имеет всегда одно и то же значение.}

_{При вычислении коэффициентов Фурье мы можем заменить промежуток интегрирования (-π, π) промежутком интегрирования (λ, λ+2π), т. е. можем положить}

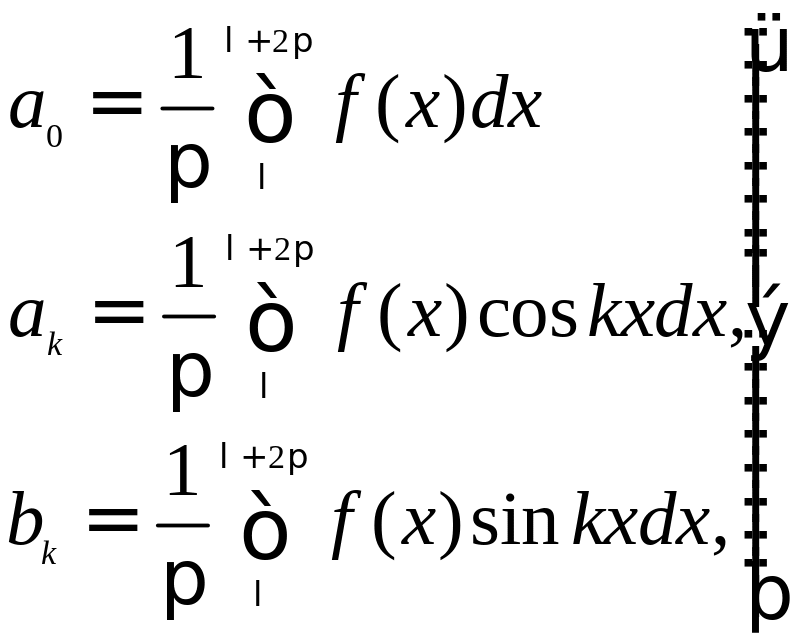(1)

_{где λ – любое число.}

_{Это следует из того, что функция ƒ(x) является, по условию, периодической с периодом 2π; следовательно и функция ƒ(x)cоsnx, и ƒ(x)sinnx являются периодическими функциями с периодом 2π. В некоторых случаях доказанное свойство упрощает процесс нахождения коэффициентов.}

_{Пример. Пусть требуется разложить в ряд Фурье функцию ƒ(x) с периодом 2π, которая на отрезке 0 <x≤ 2π задана равенством ƒ(x)=х. Эта функция на отрезке [-π, π] задается двумя формулами:}

_{В то же время на отрезке [0, 2π] гораздо проще она задается одной формулой ƒ(x)=х. Поэтому для разложения этой функции в ряд Фурье выгоднее воспользоваться формулами (1), приравняв λ=0.}

_.

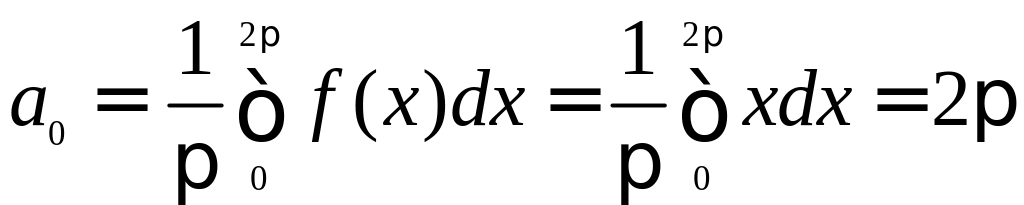
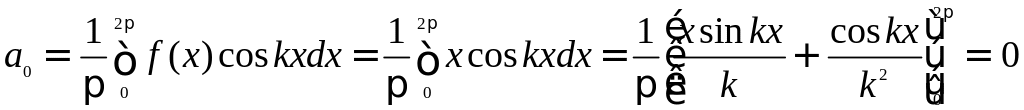
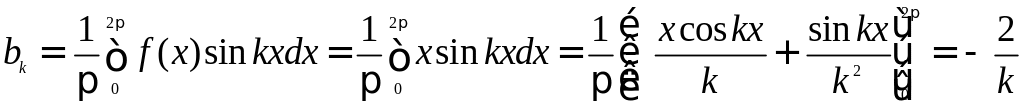_{Следовательно,}

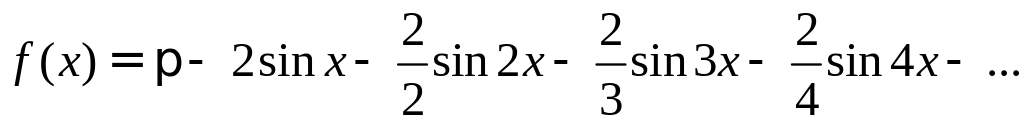
Теория рядов Фурье первоначально была создана для решения дифференциальных уравнений. Поэтому, неудивительно, что ряды Фурье широко используются для поиска решений как обыкновенных дифференциальных уравнений, так и уравнений в частных производных.

Далее рассмотрим приложение рядов Фурье к решению некоторых обыкновенных дифференциальных уравнений, а также к решению трех наиболее популярных типов уравнений математической физики:

• Уравнение теплопроводности

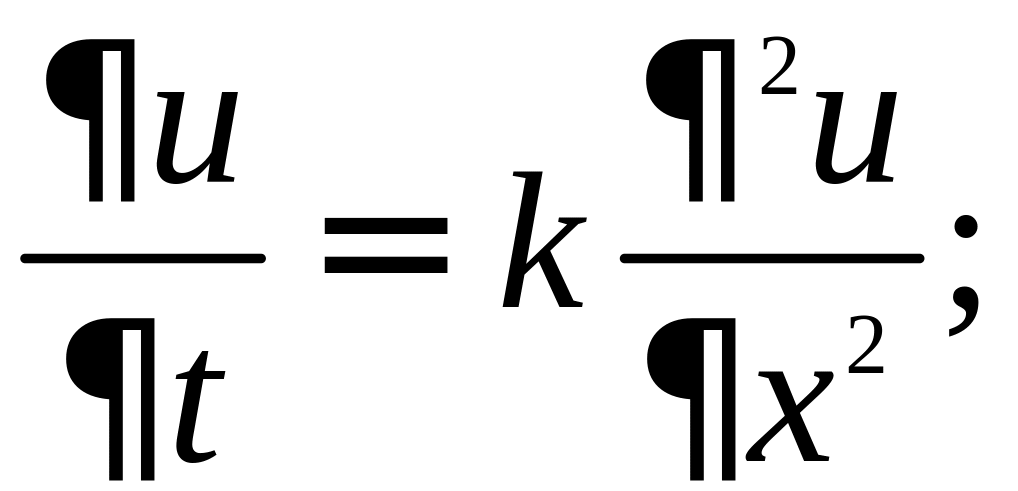
• Волновое уравнение

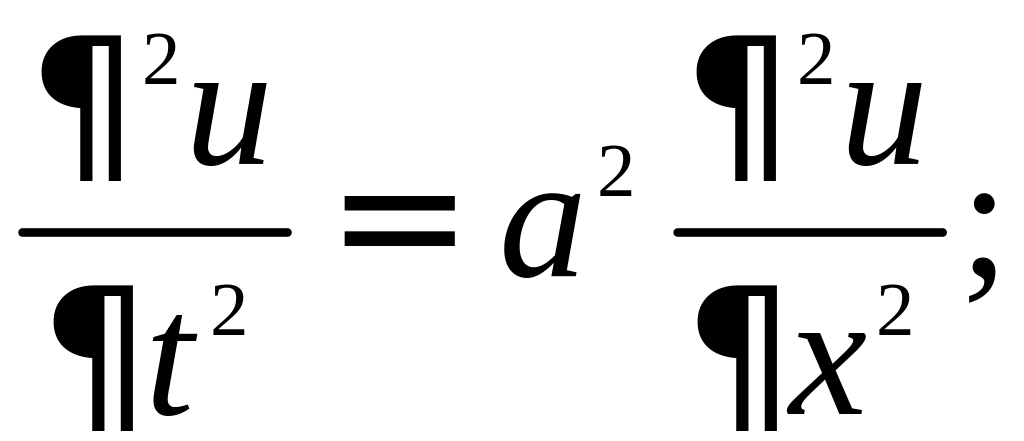
• Уравнение Лапласа

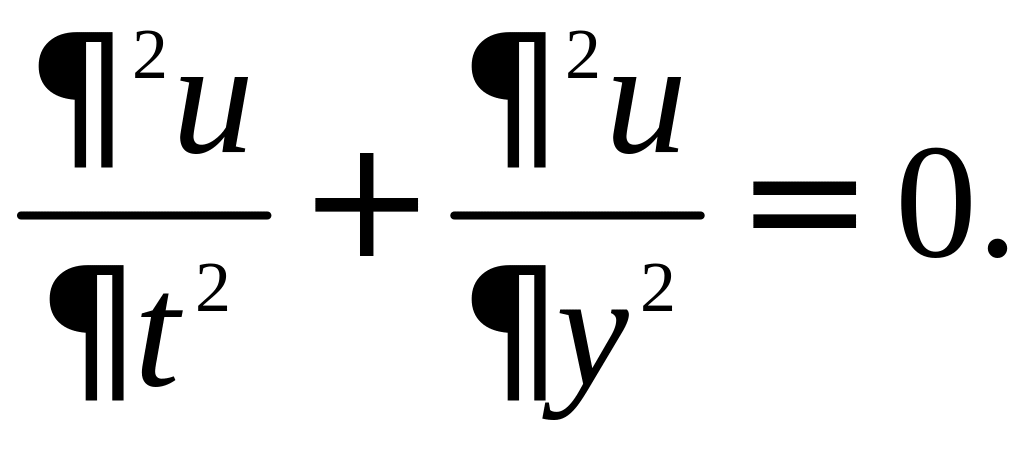
Пример. Найти решение в виде ряда Фурье дифференциального уравнения с граничными условиями

Решение.

Будем использовать разложение по нечетным гармоникам для построения неоднородного решения уравнения с заданными граничными условиями, можно записать правую часть уравнения в виде ряда 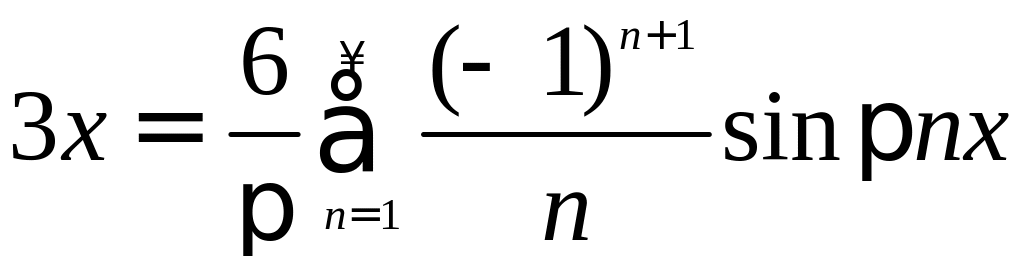. Предположим, что решение уравнения имеет вид Подставляя это в само уравнение, получаем соотношение

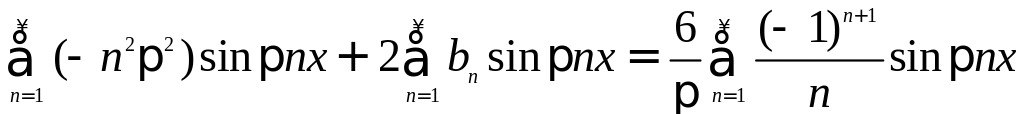
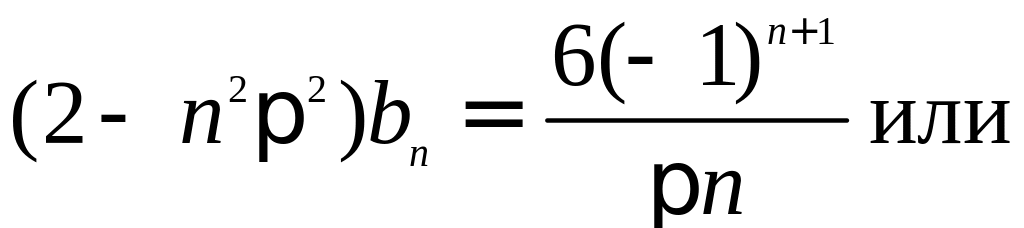
Поскольку коэффициенты при каждой гармонике в левой и правой части должны быть равны друг другу, получаем алгебраическое уравнение 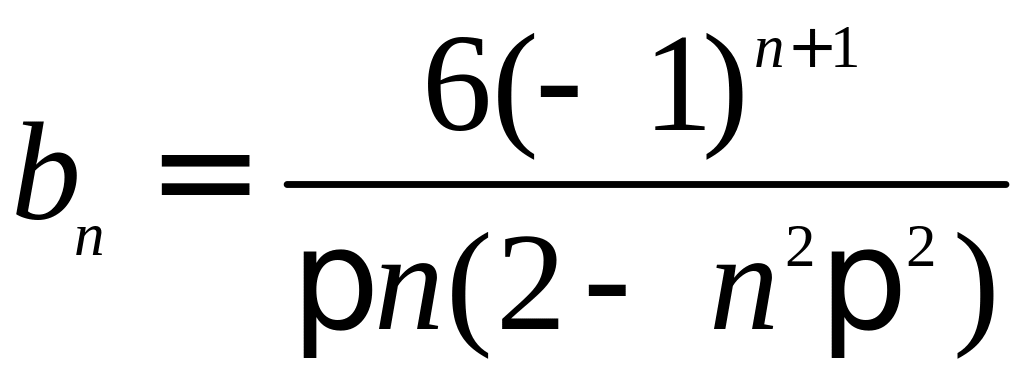. Следовательно, решение исходного дифференциального уравнения описывается рядом

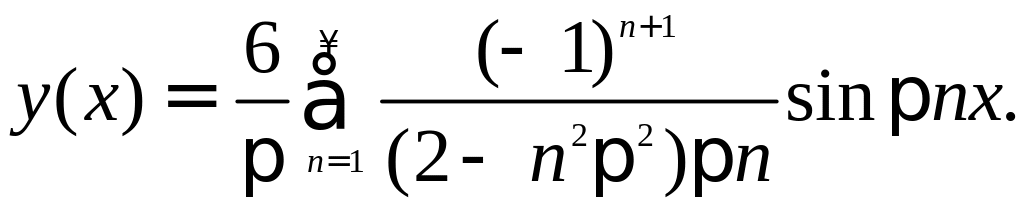
Пример. Найти периодические решения дифференциального уравнения , где k − константа, а f (x) − периодическая функция.

Решение.

Представим функцию f (x) в правой части уравнения в виде ряда Фурье:

Здесь комплексные коэффициенты Фурье определяются формулой

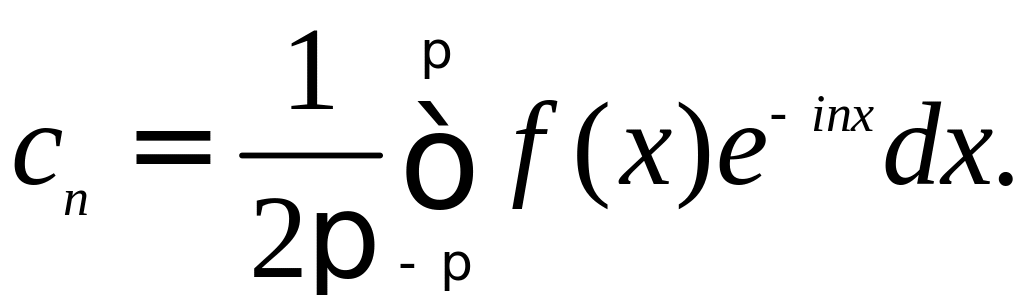
Предполагая, что решение уравнения представляется рядом Фурье Найдем выражение для производной: Подставляя это в исходное дифференциальное уравнение, получаем

Поскольку данное равенство справедливо при всех значениях n, то получаем следующее соотношение: 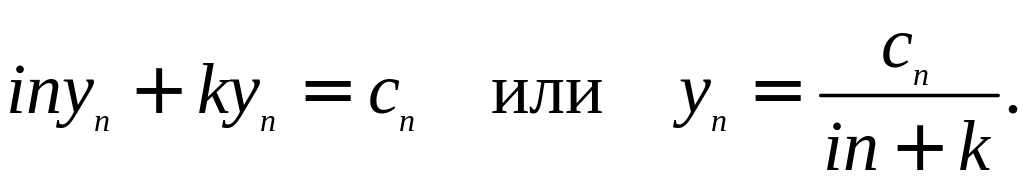Здесь c_n и k − известные числа. Следовательно, решение выражается формулой

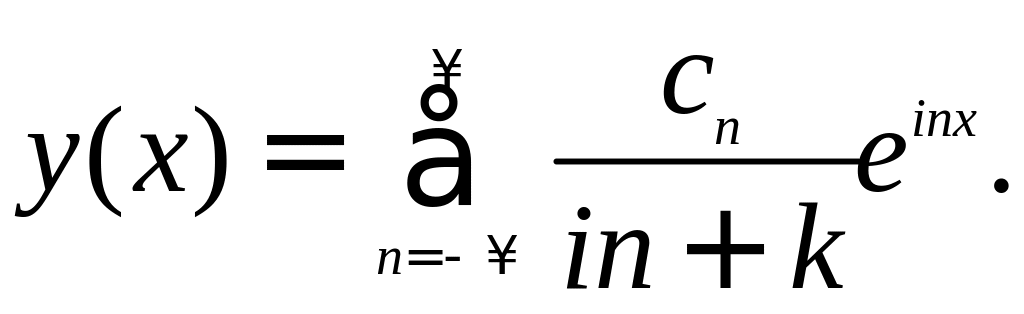
Пример.

Используя разложение в ряд Фурье, решить одномерное уравнение теплопроводности 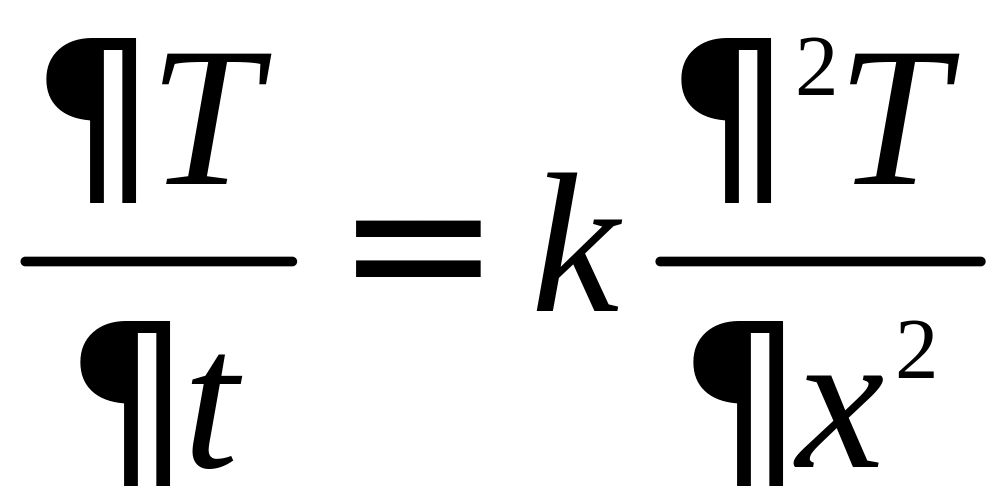с граничными условиями Дирихле: Т=Т₁ при x=0, и Т=Т₂ при x=L. Начальное распределение температуры задано функцией

Решение.

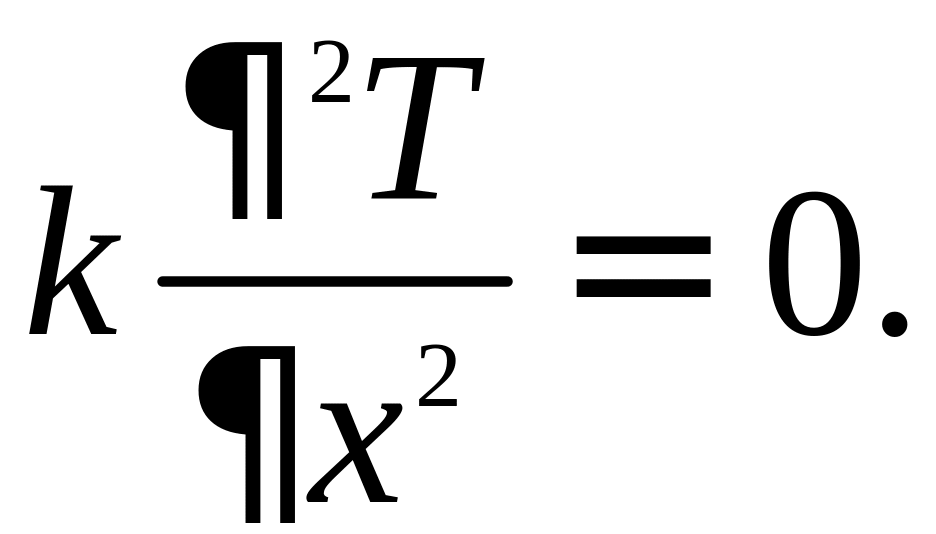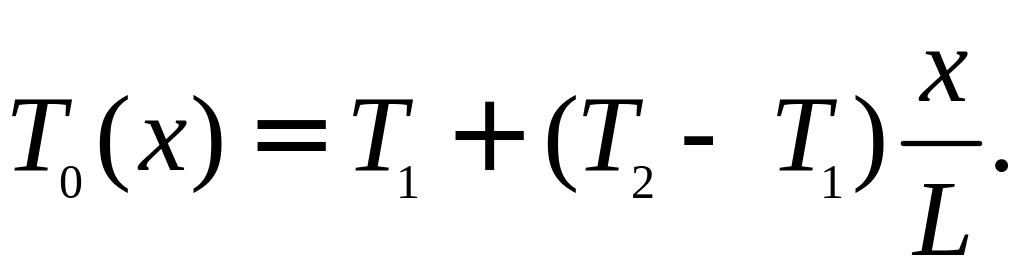Сначала мы определим стационарное распределение температуры при заданных граничных условиях. Рассмотрим уравнение Интегрируя его, найдем общее решение: Коэффициенты C₁ и C₂ найдем из граничных условий: Т₀(0)=Т₁, Т₀(L)=Т₂. В результате получаем Построим теперь решение задачи, зависящее от времени. Введем новую переменную Граничные условия для y(x,t) принимают вид: а начальное распределение записывается в форме Принимая во внимание новые граничные условия, будет естественным искать решение в виде разложения по нечетным гармоникам. Тогда 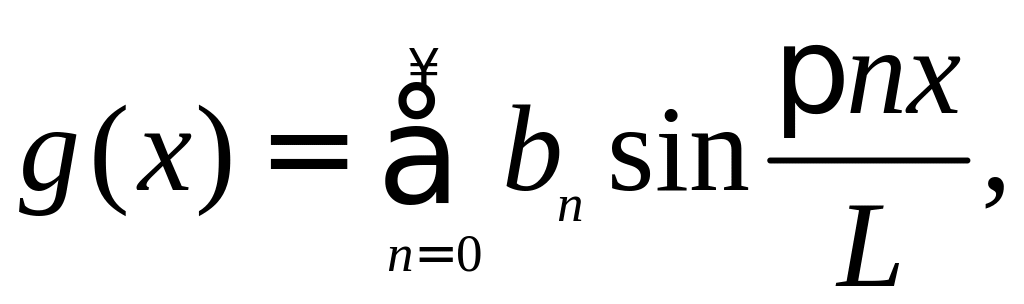где коэффициенты b_n находятся по формуле

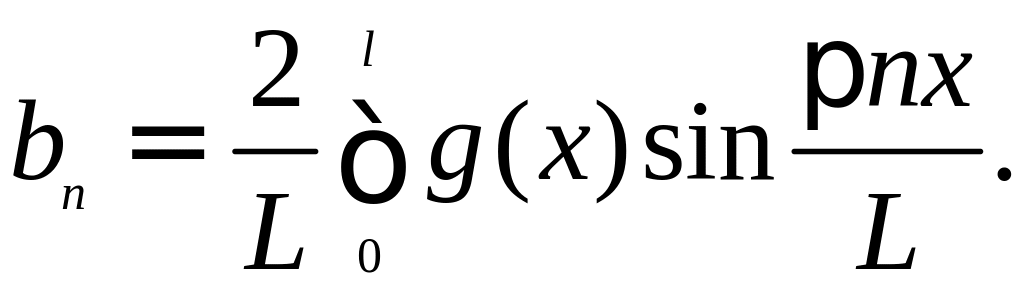
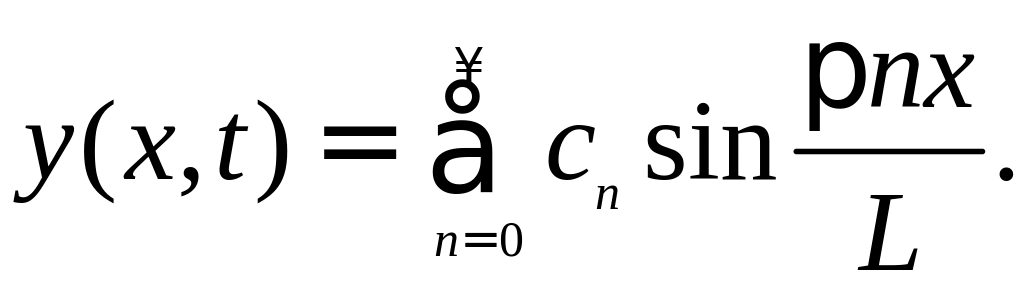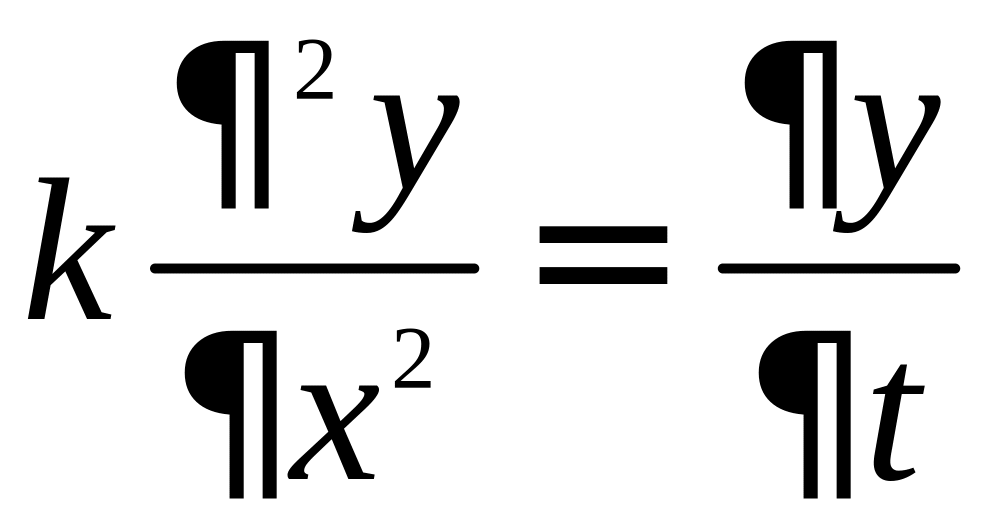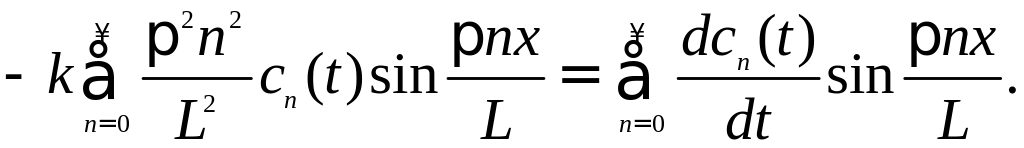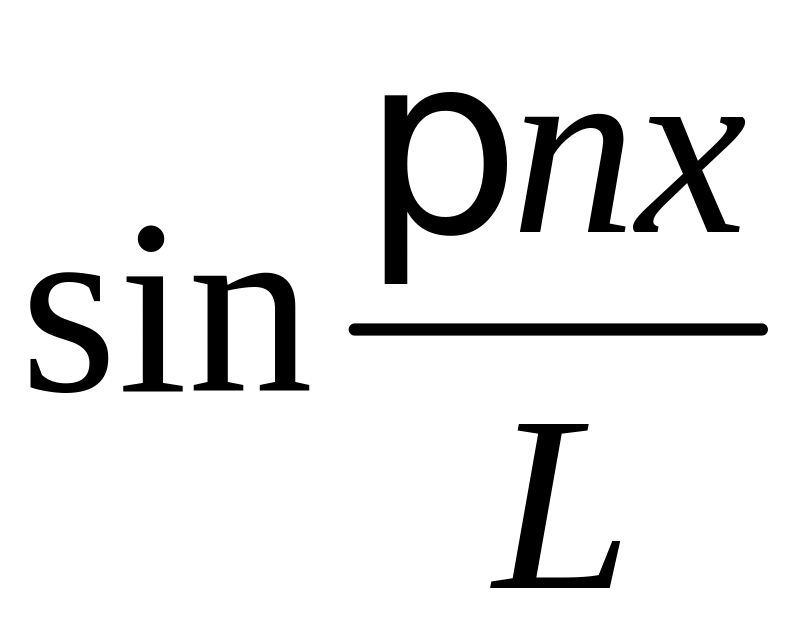(Мы предполагаем, что эти коэффициенты известны.). Общее решение будем искать в виде ряда с коэффициентами c_n(t), зависящими от времени: Очевидно, что граничные условия y(0,t)=0 и y(L,t)=0 выполняются при любых значениях времени t>0. Начальные условия для c_n(t) имеют вид Подставим эти выражения в уравнение теплопроводности . Тогда Умножим обе части последнего выражения на и проинтегрируем на интервале [0, L], используя соотношения ортогональности .
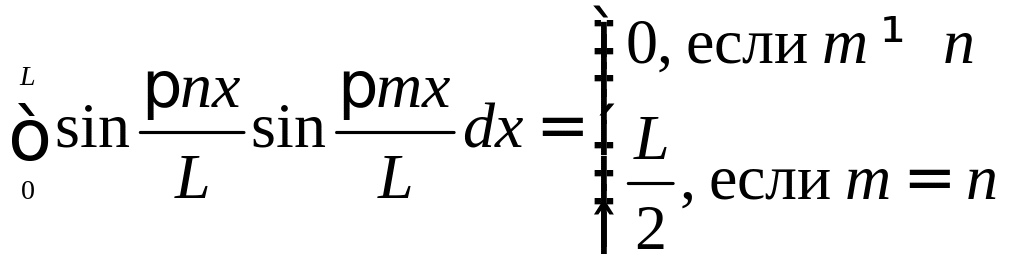