Учебники 6089

В результате получаем

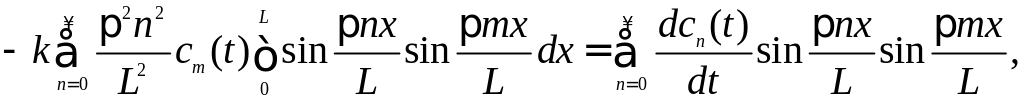или

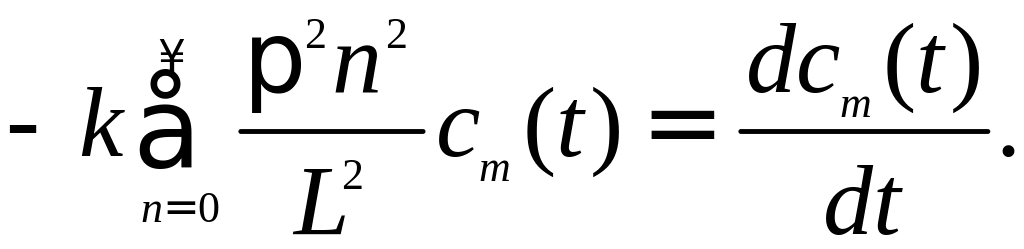
Решая полученное обыкновенное дифференциальное уравнение, находим c_n (t):

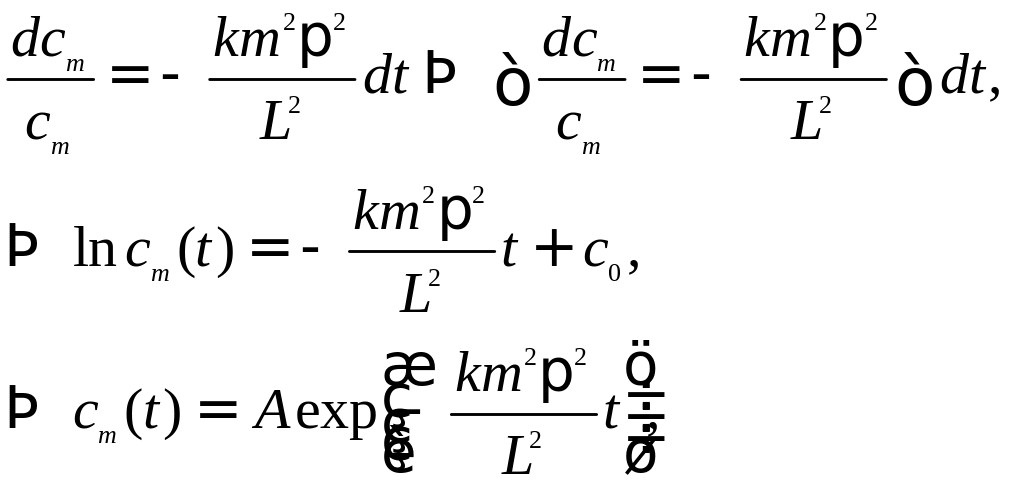
где − постоянная, зависящая от начальных условий. Учитывая, что c_n(0) =b_n, получаем решение для c_n(t) в форме

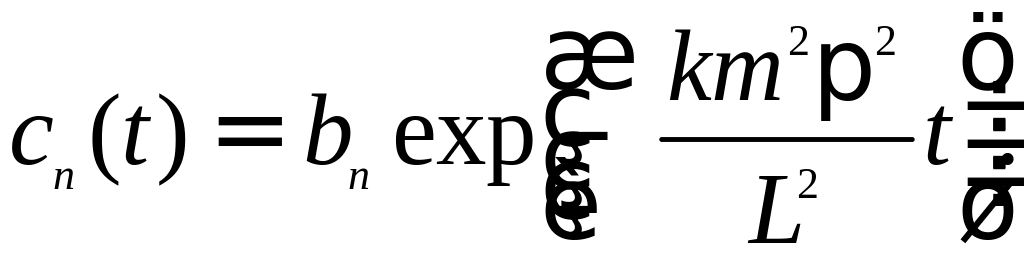
Следовательно, окончательное решение уравнения теплопроводности выражается формулой

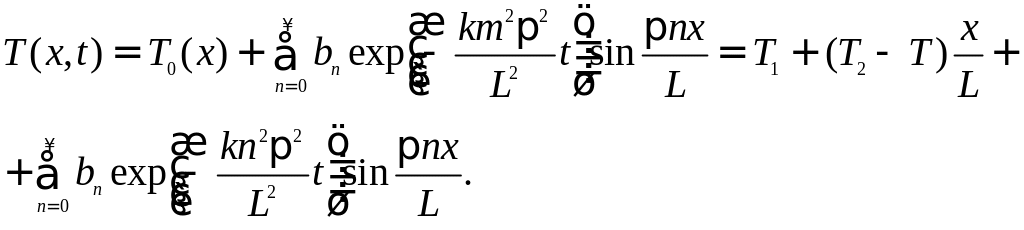
Пример.

Найти решение волнового уравнения 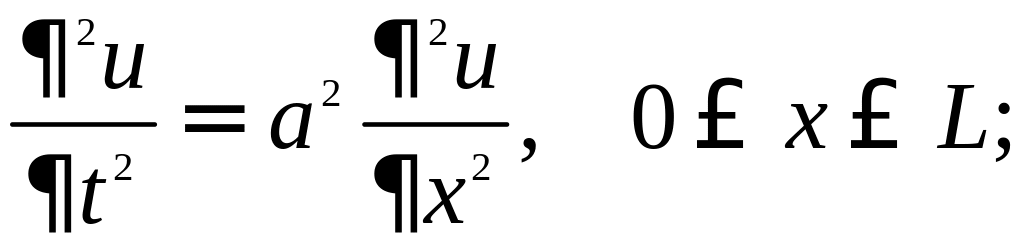для струны с закрепленными концами с граничными условиями u(0,t)=u(L,t)=0. Начальное смещение и скорость заданы в виде

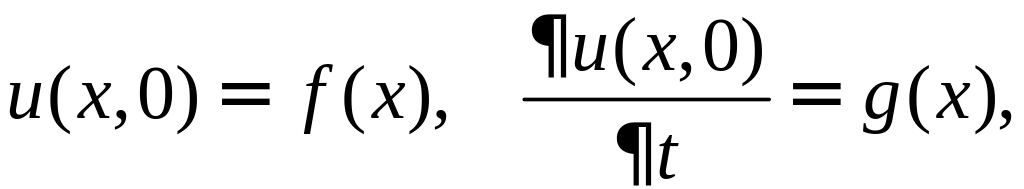где f(x) и g(x) − некоторые функции, которые считаются известными в данной задаче. При этом должны быть выполнены соотношения

Решение.

Будем искать все периодические решения задачи, в которых разделяются переменные x и t, т.е. в форме Тогда

.

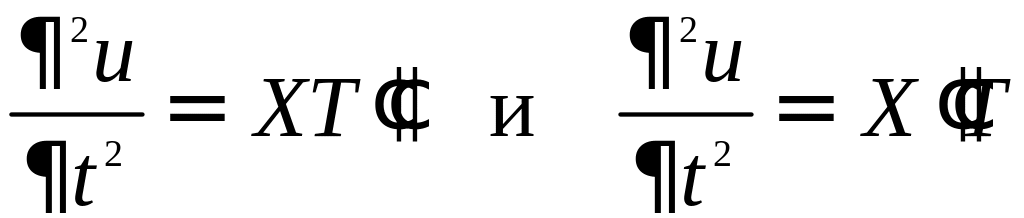Подставляя это в волновое уравнение, получаем или .

В последней записи функция в левой части зависит только от x, а функция в правой части - только от t. Это возможно, если только обе части уравнения равны некоторой константе. Следовательно,

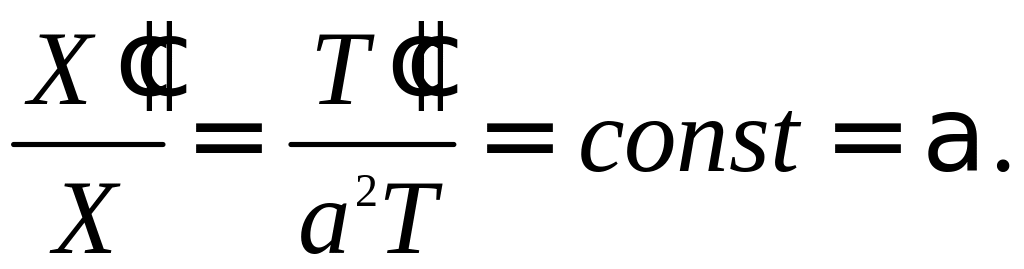
Если константа α положительная, то, полагая , получим уравнение с общим решением Такое решение не содержит периодических функций по t. Поэтому рассмотрим вариант, когда константа α отрицательна: . В этом случае волновое уравнение расщепляется на два обыкновенных дифференциальных уравнения:

Решая первое уравнение, находим: где C₁ и C₂ − постоянные интегрирования. Учитывая граничные условия, получаем: Тогда

Полагая C₂≠0 (в противном случае мы бы получили тривиальное решение X≡0), находим, что (n − целое число). Следовательно, так называемые собственные значения равны 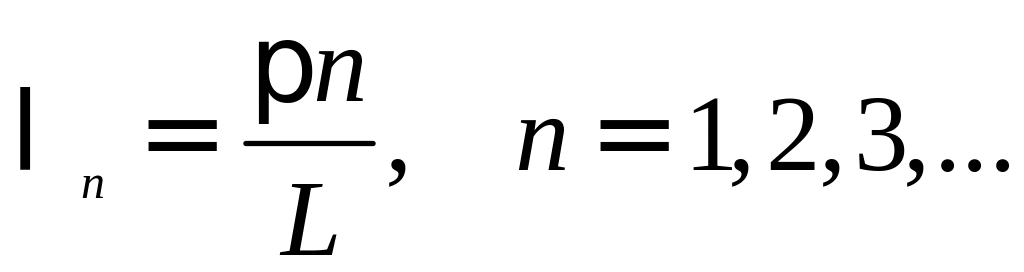Соответствующие им собственные функции записываются в виде:

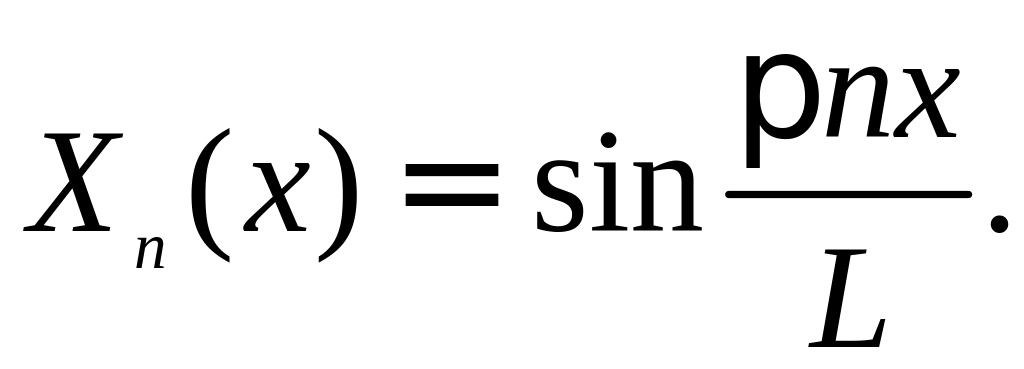
При λ=λ_n второе уравнение имеет решение

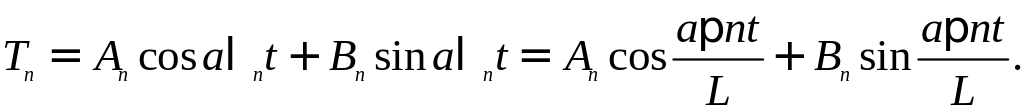
Таким образом, можно записать, что

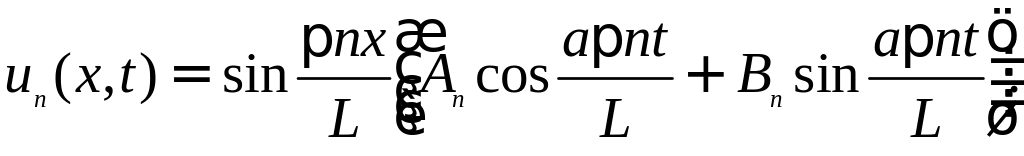
Здесь n − целое число, а A_n и B_n − постоянные, зависящие от начальных условий. Теперь мы можем построить общее решение волнового уравнения как линейную комбинацию частных решений:

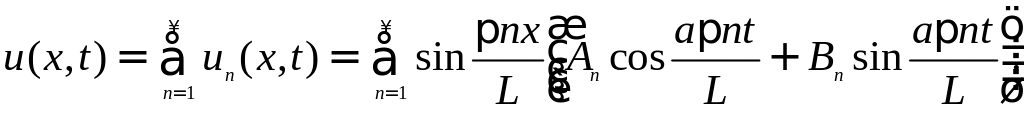
Предполагая, что этот ряд дифференцируемый, запишем выражение для производной:

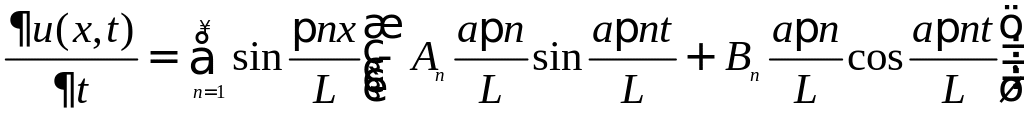
Теперь из начальных условий определим постоянные A_n и B_n:

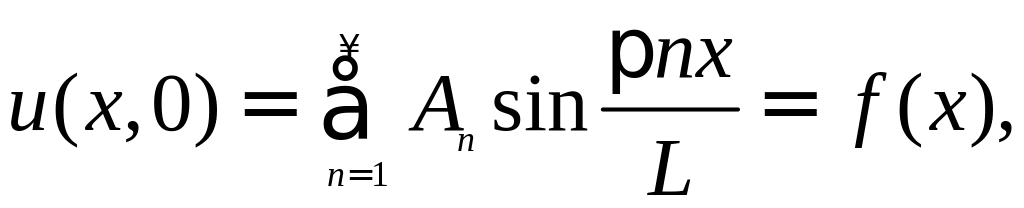
Видно, что функции f(x) и g(x) следует разложить по ортогональной системе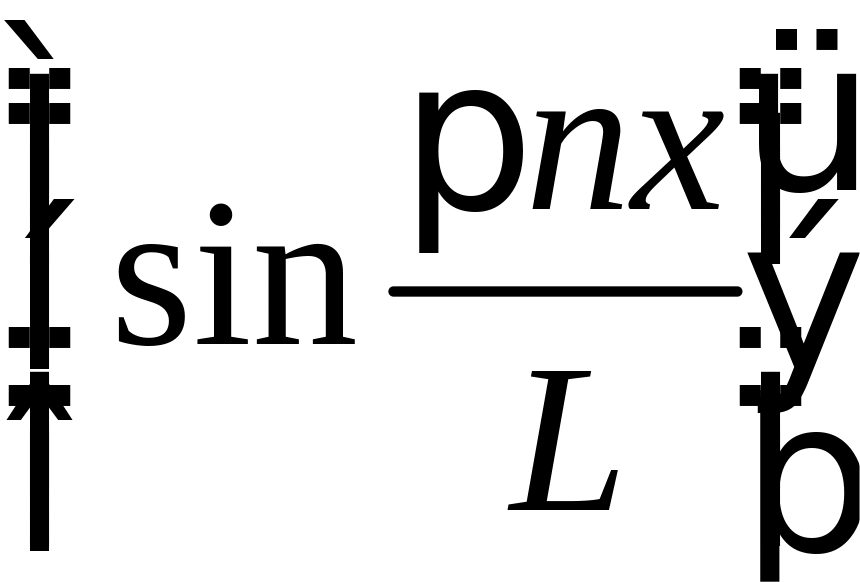 . По формулам для коэффициентов Фурье получаем:

Таким образом, решение волнового уравнения с заданными граничными и начальными условиями имеет вид:

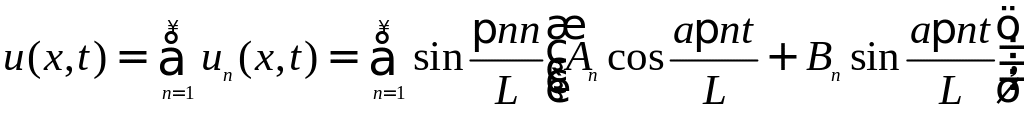
где коэффициенты A_n и B_n определяются приведенными выше формулами. Первый член ряда u₁(x,t) называется основной частотой, остальные члены u_n(x,t) − обертонами или гармониками. Период и частота гармоники определяются формулами

Пример.

Найти решение уравнения Лапласа 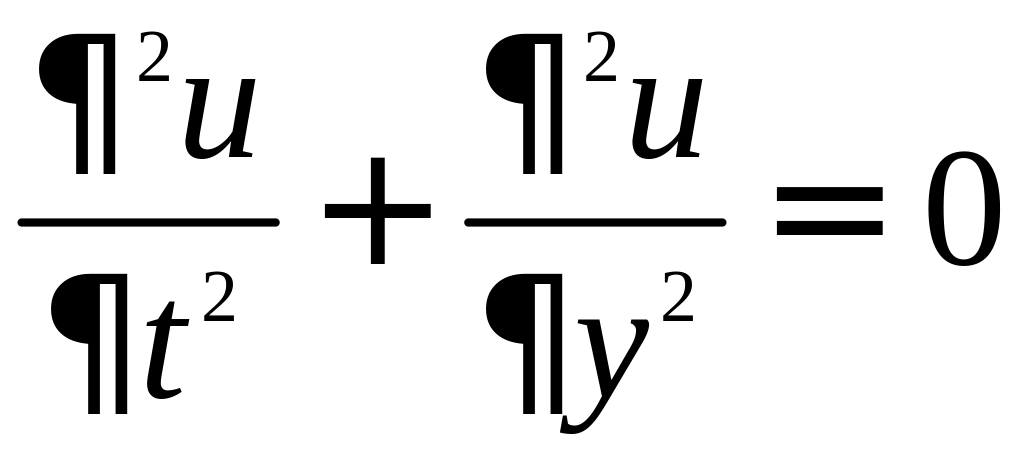в круге c граничным условием

Решение.

Будем искать решение в полярных координатах (r, φ). Взаимосвязь между декартовыми и полярными координатами определяется стандартными формулами (рисунок 3):

		Решением задачи будет функция u(r,φ), зависящая от переменных r и φ. Очевидно, u(r,φ) является 2π-периоди–ческой функцией по φ. При этом граничная функция f (x,y) преобразуется в функцию f (φ), зависящую только от пере–менной φ. Уравнение Лапласа в полярных координатах запи–сывается в виде
Рисунок 3.

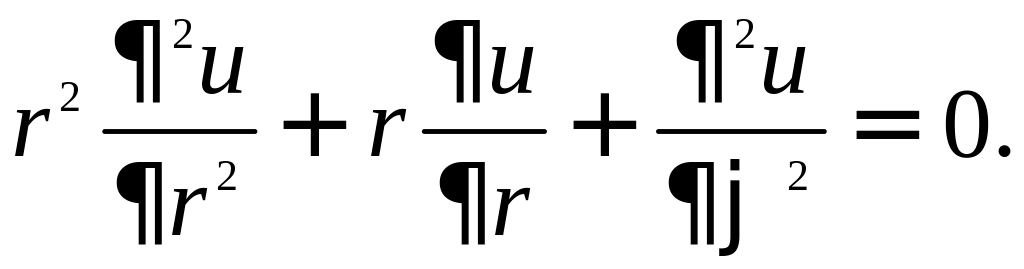
Будем искать решение u(r,φ) в виде ряда Фурье

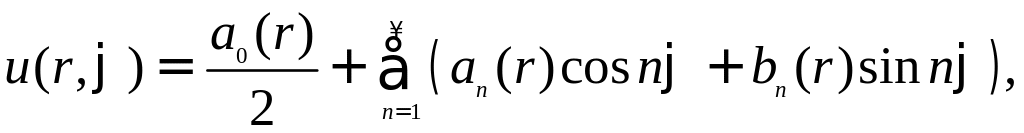
где коэффициенты Фурье a_n(r) и b_n(r) зависят от радиуса r. Предполагая, что функция u(r, φ) является достаточно гладкой и допускает двойное дифференцирование по r и φ, получаем следующие выражения для производных:

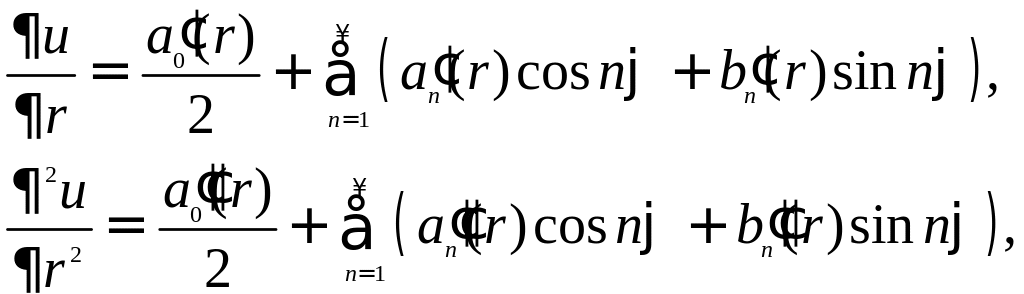
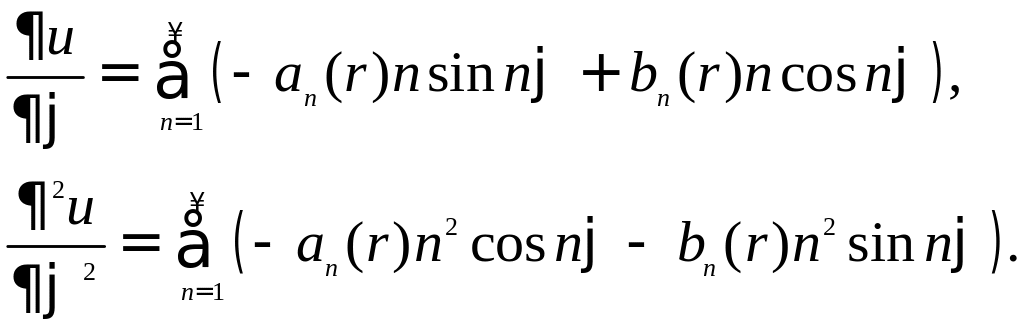
Подставляя это в уравнение Лапласа, находим

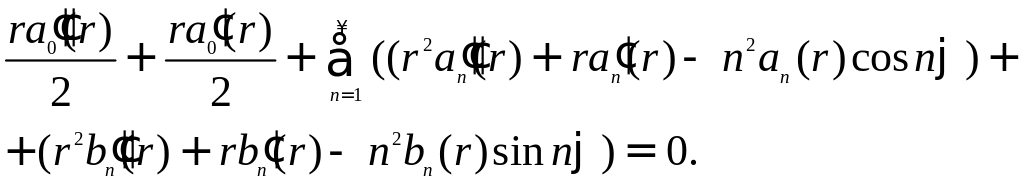
Поскольку это выражение равно нулю при всех r и φ, то приходим к выводу, что

Таким образом, мы получили систему обыкновенных дифференциальных уравнений вместо исходного уравнения в частных производных (этот метод был предложен Жозефом Фурье в 1822). Важно, что каждое уравнение в системе решается независимо. Убедимся, что полученным уравнениям удовлетворяют функции вида

Здесь постоянные a_n(r) и b_n(r) находятся из начальных условий к полученным обыкновенным дифференциальным уравнениям. Чтобы сформулировать эти начальные условия, разложим в ряд Фурье функцию , определяющую граничные условия для уравнения Лапласа в полярных координатах. В результате находим

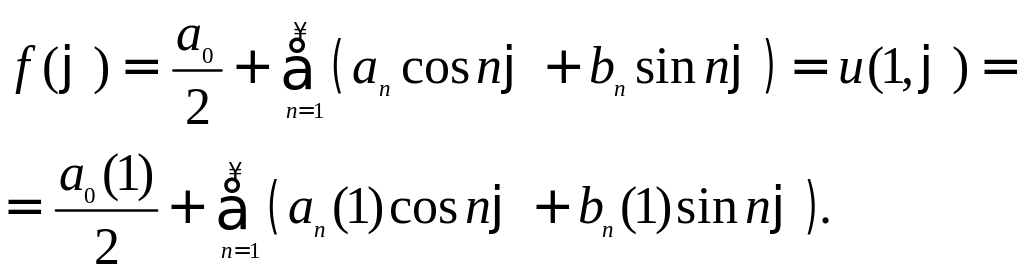
Приравнивая коэффициенты слева и справа при членах cosnφ и sinnφ, получаем соотношения

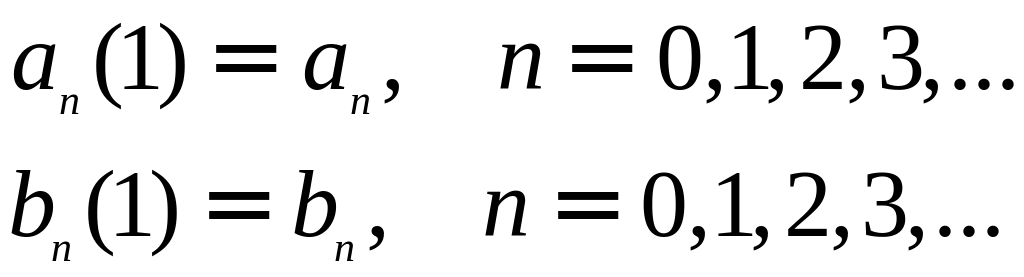
Следовательно, система обыкновенных дифференциальных уравнений имеет решение

Тогда решение уравнения Лапласа записывается в виде

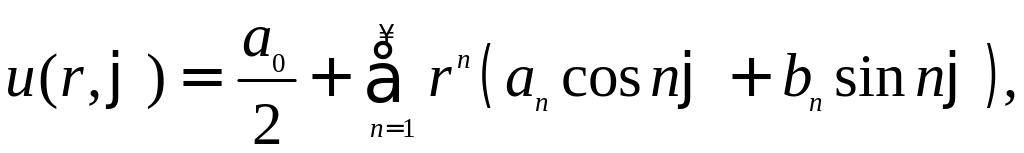
где α_n, β_n − известные числа, зависящие от граничных условий. Полученный ответ можно упростить. Подставим явные выражения для коэффициентов α_n, β_n:

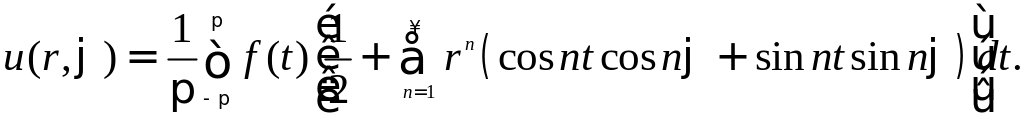
Заметим, что Поэтому

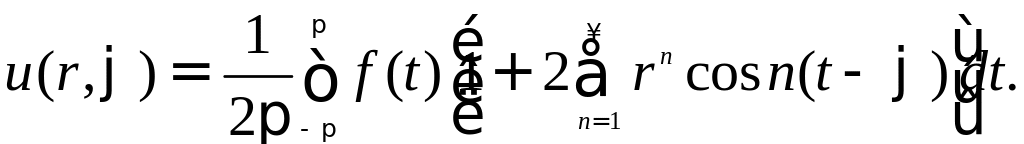
Используя формулу 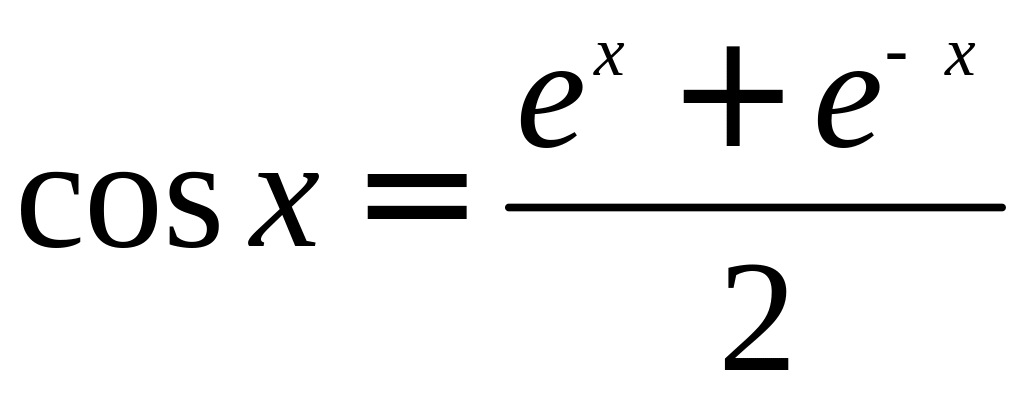, можно показать, что выражение в квадратных скобках равно сумме бесконечно убывающей геометрической прогрессии:

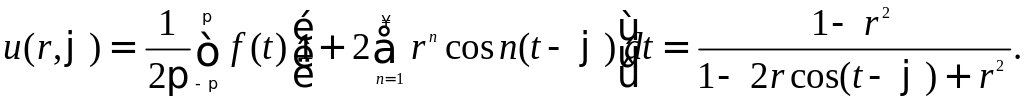
Тогда решение будет определяться формулой

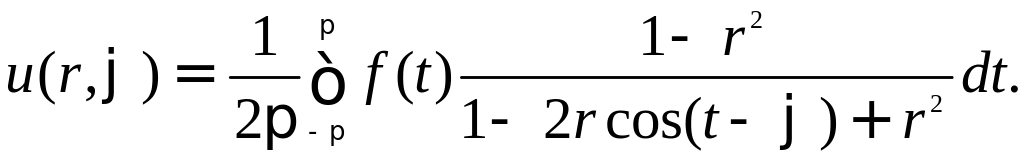
Полученное выражение называется интегралом Пуассона для единичного круга.

Библиографический список

1. Пискунов Н.С. Дифференциальное и интегральное исчисления / Н.С. Пискунов. Учебник для втузов. Т.1. - М.: Интеграл-Пресс, 2002. – 214 с.

2. Пискунов Н.С. Дифференциальное и интегральное исчисления / Н.С. Пискунов. Учебник для втузов. Т.2. - М.: Интеграл-Пресс, 2002. – 253 с.

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова: Учеб. пособие для студентов втузов. - М.: Высшая школа, 1986. Ч.2. – 136 с.

Содержание

Достаточные признаки разложимости в ряд Фурье…......................1

Ряд Фурье для четных и нечетных функций………………………..5

Разложение в ряд Фурье непериодических функций………………8

Ряды Фурье для функций любого периода ……………………........9

Ряд Фурье по ортогональной системе функций……………………10

Интеграл Фурье……………………………………………………….11

Преобразование Фурье……………………………………………….12

_{Примеры разложения функций в ряды Фурье…………………….......13}

_{Замечание о разложении периодической функции в ряд Фурье…….15}

Библиографический список…………………………………….........25

27