Учебное пособие 800619

УДК 65

ПРИМЕНЕНИЕ МАРКОВСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ К МОДЕЛИРОВАНИЮ ОРГАНИЗАЦИОННО-ТЕХНИЧЕСКИХ СИСТЕМ

А.М. Котенко, Л.П. Мышовская, А.И. Половинкина

Котенко Алексей Михайлович*, Воронежский государственный технический университет,

доктор технических наук, профессор кафедры управления

Россия, г. Воронеж, e-mail: upr_stroy_kaf@vgasu.vrn.ru, тел.: +7-473-276-40-07

Мышовская Людмила Петровна, Воронежский государственный технический университет, кандидат технических наук, доцент кафедры технологии, организации строительства, экспертизы и управления недвижимостью

Россия, г. Воронеж, e-mail: u00114@vgasu.vrn.ru, тел.: +7-960-122-22-41

Половинкина Алла Ивановна, Воронежский государственный технический университет, доктор технических наук, профессор, профессор кафедры управления

Россия, г. Воронеж, e-mail: polovinkina_alla@mail.ru, тел.: +7-473-276-40-07

Аннотация. В работе рассмотрены методы математического моделирования эволюции сложных технических систем. В основе математической модели лежит теория марковских случайных процессов с непрерывным временем и дискретным состоянием.

Ключевые слова: технические системы, марковские процессы, динамическая модель.

Введение

Большинство технических систем являются сложноструктурированными,

обладающими множеством элементов и связей, поэтому из множества методов системного анализа, для их описания наилучшим образом подходят стохастические методы, мало зависимые от степени сложности системы [3]. Если анализировать систему с точки зрения динамики ее эволюции, то из стохастических методов лучше всего подходят математические методы теории случайных процессов [2, 5].

Если техническая система может находиться в конечном числе состояний и в ней отсутствует последействие, то для ее описания можно использовать марковские случайные процессы с дискретным состоянием и непрерывным временем [4].

Целью данной работы является описание методики анализа динамики сложных технических систем с помощью математического аппарата марковских случайных процессов. При этом решим задачу для некоторой абстрактной технической системы с типичными обобщенными состояниями.

1. Математическая модель

Рассмотрим некоторую обобщенную техническую систему в виде некоторого технического устройства. Введем типичные состояния, в которых система может находиться:

S1 – нормальное функционирование системы, когда техническое устройство исправно; S2 – в системе обнаружен сбой в работе, в технической системе обнаружены

неполадки, идет диагностика;

S3 – попытка ликвидировать сбой в системе, ремонт технического устройства;

S4 – система перестала функционировать, техническое устройство списано введу невозможности ремонта (что когда-либо наступает для конечных систем.

© Котенко А.М., Мышовская Л.П., Половинкина А.И., 2019

81

Следует отметить, что можно ввести некоторые промежуточные состояния, увеличив их число, общий подход к решению не изменится, но решение в вычислительном плане усложниться.

На основании эмпирических данных, взятых в результате наблюдений за системами подобного типа и учитывая функциональные особенности работы таких систем, можно оценить следующие входные параметры системы:

T – средняя продолжительность безотказной работы системы до первого сбоя;

Td – среднее время проведения диагностики в системе, выявление причин сбоя

технического устройства, анализ возможности восстановления;

Tr – среднее время восстановления системы в случае, если это возможно;

pd – вероятность того, что после диагностики возможен возврат системы в

нормальную работу после проведения этапа восстановления;

pr – вероятность того, что в результате попытки ликвидировать сбой в системе, она

будет восстановлена на этапе ремонта.

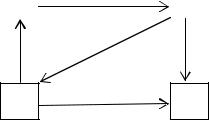
Рассмотрим простейший случай, когда случайный процесс, функционирующий в системе, будет однородным и указанные выше параметры не зависят от времени. Тогда граф состояний для описанной системы и случайного процесса представлен на рисунке.

S3 (1-pr)/Тr S4

Граф состояний системы со случайным процессом

Так как случайный процесс при длительном функционировании неминуемо перейдет в концевое состояние S4, то данный случайный процесс не является эргодическим и у него нет стационарного режима [5].

Для динамического анализа функционирования системы необходимо решить систему дифференциальных уравнений Колмогорова:

где Pi(t) (i=1, 2, 3, 4) – вероятности состояний системы.

Так как система уравнений является вырожденной, заменим четвертое ее уравнение на условие нормировки: P1(t) P2 (t) P3 (t) P4 (t ) 1. Получим:

82

Учитывая, что в начальный момент времени система нормально функционировала, уравнения Колмогорова (2) дополняются начальными условиями:

P1(0) 1; P2 (0) 0; P3 (0) 0; P4 (0) 0.

2. Определение характеристик функционирования системы

Для решения системы дифференциальных уравнений (2) примем обозначения:

В результате, с учетом начальных условий, решение (3) сводится к системе алгебраических уравнений:

83

Ее решение есть:

Выполнив обратное преобразование Лапласа, получим вероятности состояний технической системы:

P4 (t) 1 P1(t) P2 (t) P3 (t) .

В итоге, решение задачи об исследовании динамики технических систем найдено

84

Заключение

Из анализа полученного решения подтверждается то, что с течением времени вероятность всех состояний стремиться к нулю, а вероятность окончания функционирования системы (состояние S4) – к единице. При этом скорость выхода вероятностей состояний на

постоянное значение обратно пропорциональна среднему времени нормального функционирования системы до первого сбоя Т. Зависимости вероятностей состояний S2 и S3 имеют максимум при временных диапазонах порядка Td и Tr. Максимум дальше по временному интервалу, чем больше значения параметров Td и Tr. Особый интерес представляет вероятность состояния S4, когда техническая система прекращает свою

эволюцию. Эта вероятность поможет оценить длительность функционирования технической системы или время работы технического устройства.

Предложенная модель может быть использована и для иных, не технических систем [1], функционирование которых осуществляется по описанной схеме.

Библиографический список

1.Баркалов С.А. Динамическая модель потребительского спроса, основанная на марковских случайных процессах / С.А. Баркалов, С.И. Моисеев. В сборнике: «Экономическое прогнозирование: модели и методы: материалы XII международной научно- практической конференции». 2016. С. 4-7.

2.Баркалов С.А. Математические методы и модели в управлении и их реализация в MS Excel / С.А. Баркалов, С.И. Моисеев, В.Л. Порядина. - Воронежский ГАСУ. – Воронеж,

2015.- 265 с.

3.Баркалов С.А. Синтез организационной структуры управления строительным предприятием / С.А. Баркалов, П.Н. Курочка. Управление строительством. 2017. № 1 (9). С.

6-30.

4.Баркалов С.А. Модели и методы в управлении и экономике с применением информационных технологий [Электронный ресурс]: учебное пособие/ С.А. Баркалов, С.И. Моисеев, В.Л. Порядина. — СПб.: Интермедия, 2017. 264 c.

5.Вентцель Е.С. Теория случайных процессов и ее инженерные приложения / Е.С. Вентцель, Л.А. Овчаров. - М.: Высш. шк., 1998. 354 с.

6.Владимиров В.С. Уравнения математической физики. М.: Наука, 1981. — 512 с.

85

APPLICATION OF MARKOV RANDOM PROCESSES TO MODELING

OF ORGANIZATIONAL-TECHNICAL SYSTEMS

A.M. Kotenko, L.P. Myshovskaya, A.I. Polovinkina

Kotenko Alexey Mikhailovich*, Voronezh State Technical University, Doctor of Technical Sciences, Professor

Russia, Voronezh, e-mail: upr_stroy_kaf@vgasu.vrn.ru, tel.: +7-473-276-40-07

Myshovskaya Lyudmila Petrovna, Voronezh State Technical University, Candidate of Technical Sciences, Associate Professor of the Department of Technology, Organization of Construction, Expertise and Property Management

Russia, Voronezh, e-mail: u00114@vgasu.vrn.ru, tel.: +7-960-122-22-41

Polovinkina Alla Ivanovna, Voronezh State Technical University, Doctor of Technical Sciences, Professor, Professor, Department of Management

Russia, Voronezh, e-mail: polovinkina_alla@mail.ru, tel.: +7-473-276-40-07

Abstract. The paper considers methods of mathematical modeling of the evolution of complex technical systems. The mathematical model is based on the theory of Markov random processes with continuous time and a discrete state.

Keywords: technical systems, Markov processes, dynamic model.

References

1. Barkalov S.A. A dynamic model of consumer demand based on Markov random

processes [Dinamicheskaya model' potrebitel'skogo sprosa, osnovannaya na markovskikh sluchaynykh protsessakh] / S.A. Barkalov, S.I. Moiseev. V sbornike: «Ekonomicheskoye

prognozirovaniye: modeli i metody: materialy XII mezhdunarodnoy nauchno-prakticheskoy konferentsii». 2016. Pp. 4-7.

2.Barkalov S.A. Mathematical methods and models in management and their implementation in MS Excel [Matematicheskiye metody i modeli v upravlenii i ikh realizatsiya v MS Excel] / S.A. Barkalov, S.I. Moiseev, V.L. Poryadina. - Voronezh State University of Architecture and Civil Engineering. - Voronezh, 2015.- 265 p..

3.Barkalov S.A. The synthesis of the organizational structure of the construction company

[Sintez organizatsionnoy struktury upravleniya stroitel'nym predpriyatiyem] / S.A. Barkalov, P.N. Kurochka. Upravleniye stroitel'stvom. 2017. № 1 (9). Pp. 6-30.

4.Barkalov S.A. Models and methods in management and economics using information technology [Electronic resource]: a training manual [Modeli i metody v upravlenii i ekonomike s primeneniyem informatsionnykh tekhnologiy [Elektronnyy resurs]: uchebnoye posobiye]/ S.A.

Barkalov, S.I. Moiseev, V.L. Poryadina. – SPb.: Intermediya, 2017. 264 p.

5. Venttsel’ E.S. Theory of random processes and its engineering applications [Teoriya sluchaynykh protsessov i yeye inzhenernyye prilozheniya] / E.S. Venttsel’, L.A. Ovcharov. – M .:

Higher school, 1998. 354 p.

6. Vladimirov V.S. Equations of mathematical physics [Uravneniya matematicheskoy fiziki]. M.: Nauka, 1981. — 512 p.

86

УДК 378. 694.8

АЛГОРИТМ ОЦЕНКИ ИНТЕГРАЛЬНОЙ ФУНКЦИИ КАЧЕСТВА ПРОЕКТНОГО УПРАВЛЕНИЯ

Л.В. Россихина, Д.Е. Орлова

Россихина Лариса Витальевна, Воронежский институт ФСИН России, доктор технических наук,

профессор кафедры информационной безопасности телекоммуникационных систем Россия, г. Воронеж, e-mail: rossihina_lv@mail.ru, тел.: +7-960-110-56-67

Орлова Дарья Евгеньевна, Воронежский институт ФСИН России, адъюнкт Россия, г. Воронеж, e-mail: dasha_scorobogat@mail.ru, тел.: +7-906-673-92-19

Аннотация. Предложен новый алгоритм оценки интегральной функции качества проектного управления. В отличие от известных аналогов алгоритм позволяет оценить фактическое отклонение

хода его выполнения от нормы при условии корреляции локальных показателей проекта, и их оценки не только на количественных, но и качественных шкалах. Алгоритм разработан на основе

использования положений теории нечетких множеств.

Ключевые слова: управление проектами, показатель проекта, алгоритм расчета, нечисловые шкалы, норма.

Введение. Задача оценки интегральной функции качества проектного управления заключается в том, чтобы, зная множество текущих показателей, характеризующих различные стороны управляемого проекта, рассчитать обобщенную функция, характеризующую степень отклонения хода его выполнения от установленной нормы. В настоящее время для решения такой задачи используются различные методы свертки показателей, а именно, мультипликативной, аддитивной и дихотомической [1-3]. Как показывает анализ, указанные методы обладают двумя недостатками. Во-первых, все они

исходят из предположения о независимости показателей, определяющих качество проектов, что является достаточно сильным допущением. Во-вторых, они применимы только в том

случае, когда существует возможность количественно выразить значения показателей проекта, что не всегда представляется возможным и целесообразным. В статье предлагается инвариантный к проблемным областям алгоритм оценки интегральной функции качества проектного управления свободный от названных ограничений. Достигается это введением специальных метрических шкал и использованием нечетких критериев оценки качества проектного управления [4-7].

Формулировка задачи. Пусть имеется некоторый управляемый проект Q с известными локальные показатели x = {x1, x2,…, xN} и в каждый момент времени t каждому

набору xn Х соответствует состояние хода выполнения проекта s(t)S. Обозначим

символами x(X) и stec(X) функции принадлежности локальных показателей проекта и его текущего состояния соответственно.

Для определения функций x и s, а также уровня корреляции их аргументов, будем

использовать трехмерное пространство:

в котором Т – временная шкала [0, 1]; Р – оценочная шкала [0, 1]; – шкала порядка с числовым представлением [–1, +1].

Будем исходить из того, что управляемый проект находится в нормальном состоянии s* S, тогда и только тогда, когда отклонения его текущих параметров не выходят за установленные нормы. Функцию принадлежности этого состояния обозначим символом s*.

© Россихина Л.В., Орлова Д.Е., 2019

87

Тогда интегральная функция качества проектного управления tec есть множество величин

stec(X), s* и (s*, stec(X)), где (s*, stec(X)) – функция принадлежности, выражающая

степень близости текущего и нормального состояний проекта.

С учетом сказанного, задача оценки интегральной функции качества проектного управления сводится к определению функции Ωtec ( ( s*, tec (X))) и к нахождению правил

вычисления s* и (s*, stec(X)).

Решение задачи. В предположении экспоненциального характера компонентов функций s*, для расчета их значений воспользуемся выражением:

близости состояний (si,sj)[-1,+1], для оценки которой будем использовать нормированную

меру Хемминга [2,5]:

Для определения tec будем использовать пространство (1), дополнив его шкалой [+1,–1], на которой будем измерять степень близости состояний проекта, то есть величины . (si,sj).Тогда интегральную оценку близости состояний управляемого проекта за один шаг

его выполнения можно рассчитать с помощью интеграла Стилтьеса [9], который в нашем имеет вид:

С учетом (2-4) суть алгоритма оценки интегральной функции качества проектного управления сводится к выполнению следующих шагов:

Шаг 1. Определение по формуле (2) функции принадлежности параметров проекта к

нормальному состоянию s*.

Шаг 2. Определение по формуле (3) функции принадлежности близости текущего и

нормального состояний проекта (s*, stec(X)).

Шаг 3. Определение по формуле (4) интегральной функции качества проектного

управления.

Заключение. Предложенный в статье алгоритм построен на положениях теории нечетких множеств. Это дало возможность оценить интегральную функцию качества проектного управления при условии корреляции локальных показателей выполняемого проекта и невозможности их представления на количественных шкалах. Алгоритм и входящие в него расчетные соотношения инвариантны к проблемным областям проектного управления и могут быть использованы при разработке программных средств интеллектуальной поддержки проектных решений в социальных и экономических системах.

88

Библиографический список

1. Шабалин А.Н. Инвестиционное проектирование. – М.: Изд-во МЭСИ, 2002. –

320 с.

2.Порядина В.Л. Управление социально-экономическими проектами: конкурсный

подход. – Воронеж: Научная книга, 2015. – 230 с.

3.Орлова Д.Е., Крупенко С.Е. Интегральная оценка строительных проектов методом иерархической дихотомии. Вестник Воронежского института высоких технологий. 2014. № 12. С. 54-56.

4.Заде Л.А. Понятия лингвистической переменной и его применение к принятию приближенных решений. – М.: Мир, 1976. – 165 с.

5.Борисов А.Н., Крумберг О.А., Федоров И.П. Принятие решений на основе нечетких моделей: Примеры использования. – Рига: Зинатне, 1990. –184с.

6.Вересков А.А., Кузькин В.Б., Федоров В.В. Определение степеней принадлежности на основе совокупности матриц Саати для нечетких множеств // Сб.тр. ВНИИСИ. – М., 1982. – №10. С. 117-124.

7.Жаке-Лагрез Э. Применение размытых отношений при оценке

предпочтительности распределенных величин // Статистические модели и многокритериальные задачи принятия решений. – М.: Статистика, 1979. С.168-183.

8.Аржакова Н.В., Новосельцев В.И. Определение интегральной оценочной функции диагностируемой системы на основе нечетких представлений / Моделирование систем и информационные технологии. Сб. науч. тр. ВИВТ – Воронеж: Изд-во Научная книга, 2004. – Вып.1. – С. 20-28.

9.Левиатов А.Ю., Захаров В.Н. Непрямые методы диагностики // Международный симпозиум по искусственному интеллекту. – Л.: ISAI, 1983. – С.67-72.

89

ALGORITHM OF ESTIMATION OF INTEGRAL FUNCTION OF QUALITY OF

PROJECT MANAGEMENT

L.V. ROSSIKHINA, D.E. ORLOVа

Rossikhina Larisa Vitalievna, ET Department, Voronezh Institute Federal Penitentiary Service of Russia, 1a Irkutskaya Street, RU, Voronezh, e-mail: rossihina_lv@mail.ru, тел.: +7-960-110-56-67

Orlova Darya Evgenievna, ET Department, Voronezh Institute Federal Penitentiary Service of Russia, 1a Irkutskaya Street, RU, Voronezh, e-mail: dasha_scorobogat@mail.ru, тел.: +7-906-67-39-219

Abstract. A new algorithm for estimating the integral function of project management quality is proposed. In contrast to the known analogues, the algorithm allows to estimate the actual deviation of the progress of its implementation from the norm, provided the correlation of local indicators of the project, and their evaluation not only on quantitative but also qualitative scales. The algorithm is developed on the basis of using the provisions of the theory of fuzzy sets.

Keywords: project management, project indicator, calculation algorithm, non-numeric scales, norm.

REFERENCES

1. Shabalin A. N. [Investment planning]. – M:. publishing house of the University, 2002. –

320 p.

2.Poryadina V. L. [Management of socio-economic projects: a competitive approach]. – Voronezh: Scientific book, 2015. – 230 p.

3.Orlov, D. E., Krupenko S. E. [Integrated evaluation of construction projects by the method of hierarchical dichotomies]. Bulletin of Voronezh Institute of high technologies. 2014. No.

12.Pp. 54-56.

4.Zadeh L. A. [Concept of linguistic variable and its application to making approximate decisions]. – M.: Mir, 1976. – 165 p.

5.Borisov A. N., Grumberg O. A. and Fyodorov I. P. [decision-Making based on fuzzy models: Examples of use]. – Riga: Zinatne, 1990. –184с.

6.Vereskov A. A., Kuzkin V. B., Fedorov V. V. [Determination of grades of membership based on the totality of Saaty matrices for fuzzy sets] // Proc.Tr. VNIISI. – M., 1982. – No. 10. P. 117-124.

7.Jacques-of Logres E. [Application of fuzzy relations in the assessment of preference distributed values] // Statistical models and multi-criteria decision-making tasks. – M.: Statistics, 1979. P. 168-183.

8.Arzhakova N. In. Novoseltsev, V. I., [Determination of an integral evaluation function of

the diagnosed system based on fuzzy representations / Modeling systems, and information technology][. SB. scientific. Tr. Military hardware – Voronezh: publishing house of Scientific book, 2004. – Vol.1. – S. 20-28.

9.Levitov A. Yu., Zakharov V. N. Indirect diagnostic methods // international Symposium on artificial intelligence]. – L.: ISAI, 1983. – P. 67-72.

90