
Сборник задач по алгебре. Майорова С.П., Завгородний М.Г
.pdf170. Исследуйте и решите сравнения:
1) |
127x 80 (mod 274) ; |
2) |
36x 42 (mod 90) ; |
|
3) |
83x 12 (mod101) ; |
4) |
820x 13 (mod 9) ; |
|
5) |
78x 42 (mod 51) ; |
6) |
415x 200 (mod 630) ; |
|
7) |
134x 118 (mod 206) ; |
8) |
111x 75 (mod 321) ; |
|
9) |
67x 64 (mod183) ; |
10) |
354x 567 (mod 639) ; |
|
11) |
2775x 825 (mod 624) ; |
12) |
285x 177 (mod 924) ; |
|
13) |
285x 51 (mod 363) ; |
14) |
12103x 385 (mod1425) ; |
|
15) |
89x 86 (mod 241) ; |
16) |
186x 374(mod 422) ; |
|
17) |
486x 39 (mod 327) ; |
18) |
690x 57 (mod 429) ; |
|
19) |
213x 137 (mod 516) ; |
20) |
1296x 1105 (mod 2413) . |
|
171. Решите сравнения способом подбора:
1) |
x4 3x3 x2 2 0 |
(mod 7) ; |
2) |
x3 |
7x 3 0 |
(mod 5) ; |
|
||||||
3) |
x3 x 1 0 |
(mod 6) ; |
4) |
x2 |
3x 5 0 |
(mod 5) ; |
|
||||||
5) |
x5 x 1 0 |
(mod 7) ; |
6) |
x3 |
3x 1 0 |
(mod19) . |
|
||||||
|
172. Решите системы сравнений: |
|
|
|
|
|
|
||||||
1) |
x 3 (mod12) |
; |
|
2) |
x 2 (mod 15) |
; |
3) |
x 28(mod15) |
; |
||||
|
|
|
|
|
|
|
|
||||||
|
x 4 (mod 5) |
|
|
|
x 18 (mod 22) |
|
|
x 18(mod 22) |
|
|
|||
4) |
3x 2(mod 5) |
; |
5) |
4x 7(mod11) |
; |
6) |
4x 3(mod 7) |
; |
|
||||
|
|
|
|
|
|
|
|
||||||
|
2x 5(mod 9) |
|
|
8x 15(mod13) |
|
|
5x 4(mod 6) |
|
|
||||
|
x 7(mod 5) |
|
x 16 (mod 5) |
|
7) |
|
; 8) |
|
; |
x 3(mod 4) |
x 27 (mod 4) |
|||
|
|
|
|
|
|
x 26(mod11) |
|
x 2 (mod13) |
|
x 15(mod 7) 9) x 8(mod 5) ;x 19(mod11)
7x 5(mod11) |
7x 10(mod11) |
5x 20(mod 6) |
|
10) 13x 12(mod 23) ; 11) 12x 7(mod13) ; |
12) 6x 6(mod |
5) . |
|
5x 2(mod 7) |
7x 11(mod15) |
4x 5(mod |
77) |
|
|
|
|
41
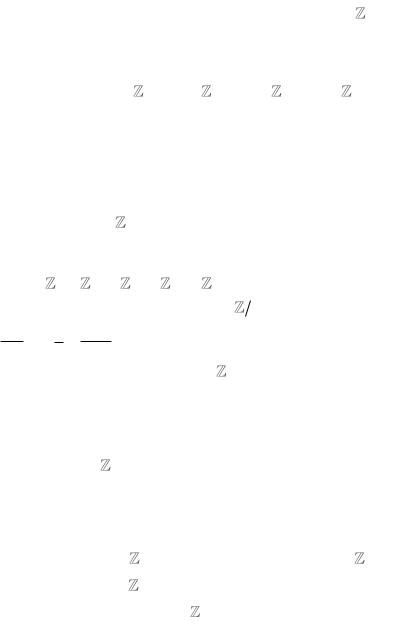
173. Укажите, из каких элементов состоит кольцо 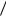 10 .
10 .
Выпишите множества всех обратимых элементов и всех делителей нуля этого кольца. Для каждого обратимого элемента найдите обратный.
174. Для колец 1) 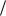 11, 2)
11, 2) 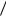 16 , 3)
16 , 3) 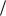 20 , 4)
20 , 4) 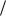 28
28
укажите множества всех обратимых элементов и всех делителей нуля. Для каждого обратимого элемента найдите обратный. Для элементов [a]m , являющихся делителями нуля,
найдите [b]m [0]m такой, что [a]m [b]m [0]m . Является ли такой класс [b]m единственным?
175. Для кольца |
360 |
найдите: 1) число обратимых эле- |
|
ментов; 2) число делителей нуля. |
|||
176. |
Укажите, какие из данных колец вычетов являются |
||
полями: |
8 , 15 , |
19 , |
47 , 129 . |
177. |
В кольце классов вычетов 117 найдите сумму, |
||
произведение и обратные (если они существуют) для классов a 248 и b 416 .
178. В кольце классов вычетов 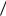 14 найдите сумму, произведение и обратные (если они существуют) для классов:
14 найдите сумму, произведение и обратные (если они существуют) для классов:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
|
319 и |
35 ; |
2) |
17 и |
31; |
3) |
16 |
|
и |
|
271; |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4) |
|
219 и |
201 ; |
5) |
102 |
и 35 ; |
6) |
131 |
и |
262 . |
|
||||||||||||||||||
|
|
179. В кольце |
18 |
вычислите: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1) |
318 72 |
15 5 1 ( 21) 35 ; |
|
|
2) 15 715 |
12 75 730 7 ; |
|||||||||||||||||||||||
3)710 79 78 .
180.Вычислите значение выражения в указанном поле:
1) |
(2 6 3 5)10 |
в поле |
7 ; |
2) (1 2 3 4) 2 в поле 11 ; |
3) |
(7 3 1 4) 1 |
в поле |
13 ; |
|
4) |
1 1 2 1 ... ( p 1) 1 |
в поле |
p ( p 2 ). |
|
42

|
|
181. Для матрицы A над данным полем |
p |
найдите |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
обратную матрицу A 1 . Сделайте проверку. |
|
|
|
|
|
|
|||||||||||||
|
|
3 |
2 |
|
|
|
|
|
|
8 |
7 |
|
|
|
|
|
|
||
1) |
A |
|
|
над |
7 ; |
|
2) |
A |
|
|
над |
13 ; |
|
|
|
||||
|
|
|
1 |
6 |
|
|
|
|
|
|
|
3 |
5 |
|
|
|
|
|
|
|
|
7 |
5 |
|
|
|
|
|
|
1 |
2 |
5 |
|
|
|
|
|||
|
|
|
|
11 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|||
3) |
A |
|
|
над |
|
4) |
A |
4 |
0 |
1 |
над 7 ; |
|
|
||||||
|
|
|
1 |
3 |
|
|
|
|
|
|
|
3 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
5 |
2 1 |
|
|
|
|
1 |
0 1 1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 . |
|
5) |
A |
8 |
3 |
6 |
над 31 ; |
|
6) |
A |
0 |
1 |
0 |
1 над |
|||||||
|
|
|
7 |
4 |
5 |
|
|
|
|
|
|
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
|
|
|
|
|
|
182. Найдите ранг данной матрицы над данным полем: |
|||||||||||||||||
|
2 3 |
1 4 5 |
|
|
1 2 |
1 1 0 |
|
|
|
||||||||||
|
|
1 2 |
0 |
6 |
3 |
|
|
|
|
2 1 |
0 |
2 |
1 |
|
|
|
|
||
1) |
над |
7 |
; 2) |
над |
3 |
. |
|||||||||||||
|
|
3 3 |
5 0 2 |
|
|
|
1 2 |
2 1 1 |
|
|
|
||||||||
|
|
|
|
|
|
||||||||||||||
|
|
2 4 |
4 3 5 |
|
|
|
|
0 0 |
1 0 1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
183. Решите уравнение в указанном поле: |
|
|
|
||||||||||
1) |
3x 7 0 в поле |
17 ; |
|
|
|
2) 5x 11 0 в поле 19 ; |
|
|||||||
3) |
4x2 x 2 0 в поле |
|
7 |
; |
4) 2x2 4x 1 0 в поле |
5 |
; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5) |
x3 x 2 0 в поле |
5 |
; |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6) |
x4 3x3 4x 5 0 в поле |
7 |
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
184. Решите системы линейных уравнений: |
|
|
|
||||||||||
1) над полем |
2 : |
|
|
|
|
|
|
|
|
|
|
|
||
|
x |
x |
x |
x |
1 |
|
x |
x |
x |
x |
1 |
|
||
|
1 |
2 |
3 |
4 |
|
|
|
|
1 |
2 |
3 |
4 |
|
|
а) x1 |
|
x3 |
|
1 ; |
б) x1 |
|
x3 |
|
1; |
|
||||
|
|
x2 |
|
x4 |
0 |
|
|
x2 |
|
x4 |
1 |
|
||
|
|
|
|
|
|
|
||||||||
43

2) над полем |
3 : |
|
|
|
|
|
|
|
x |
x |
x |
1 |
2x |
x |
x |
1 |
|
1 |
2 |
3 |
|
|
1 |
2 |
3 |
|
а) 2x1 |
x2 |
x3 |
1 ; |
б) 2x1 |
x2 |
2x3 |
2 ; |
|
|
2x |
2x |
1 |
2x |
2x |
x |
0 |
|
|
2 |
3 |
|
|
1 |
2 |
3 |
|
3) над полем |
5 : |
|
|
|
|
|
|
|
x |
2x |
4x |
1 |
x |
x |
x |
2 |
|
1 |
2 |
3 |
|
|
1 |
2 |
3 |
|
а) x1 |
3x2 |
4x3 |
2 ; |
б) 2x1 |
3x2 |
4x3 |
1 . |
|
x |
4x |
x |
3 |
3x |
|
2x |
0 |
|
1 |
2 |
3 |
|
|
1 |
|
3 |
|
|
185. |
Решите системы уравнений над данным полем. |
||||||||
Сделайте проверку. |
|
|
|
|
|
|
|
|||
1) |
3x 4 y 1 |
над |
13 ; |
|
2) |
4x 5 y 6 |
над 11 . |
|||
|
3y 7 |
|
|
7x 3y 1 |
||||||
|
5x |
|
|
|
|
|
|
|
||
|
186. |
Решите матричное уравнение над полем |
|
7 , сде- |
||||||
лайте проверку: |
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
2 |
4 |
|
3 |
|
|
|
|
|
|
|
X |
|
. |
|
|
|
|
|
|
|
1 |
4 |
1 |
1 |
|
|
|
|
187. |
Докажите, что ненулевой элемент [a]m |
m обра- |
|||||||
тим тогда и только тогда, когда числа a и m взаимно просты, и что в противном случае [a]m является делителем нуля.
188. При каком m в кольце 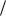 m возможно равенство
m возможно равенство
[2]m [3]m [5]m ?
189.Найдите условия, при которых все элементы группы
 m; являются кратными одного ее элемента [a]m .
m; являются кратными одного ее элемента [a]m .
Сколько таких элементов существует в группе 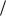 m; ?
m; ?
44

|
КОЛЬЦО МНОГОЧЛЕНОВ |
|
|
|
|
|||||||
|
190. Для многочленов |
f (x) и g (x) над данным полем P |
||||||||||
разделить с остатком f (x) |
на g (x) : |
|
|
|
|
|
||||||
1) |
f (x) x4 3x3 5x2 6x 7 , |
g(x) x2 x 3 , |
P ; |
|||||||||
2) |
f (x) x5 1 , g(x) x3 1 , |
P ; |
|
|
|
|
|
|||||
3) |
f (x) 2x4 3x3 4x 1 , |
g(x) 3x3 x 2 , |
P |
5 |
; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4) |
f (x) x5 x3 x 1, |
g(x) x3 x 1 , |
P |
2 |
. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
191. В кольцах |
3[x] , |
5[x] , |
[x] |
найдите частное и |
|||||||
остаток при делении многочлена |
f (x) на многочлен g (x) : |
|||||||||||
1) |
f (x) x5 x2 x 1, |
g(x) x3 2x 1 ; |
|
|
|
|
||||||
2) |
f (x) 2x4 x2 2x , |
g(x) x2 2 . |
|
|
|
|
|
|||||
|
192. Разделить |
многочлен |
f (x) |
[x] |
с остатком на |
|||||||
(x x0 ) и найти значение |
f (x0 ) : |
|
|
|
|
|
|
|
||||
1) |
f (x) x4 2x3 4x2 6x 8 , |
x 1 ; |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
2) |
f (x) 2x5 5x3 8x , |
x 3 ; |
|
|
|
|
|
|
||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
3) |
f (x) 3x5 x4 19x2 13x 10 , |
x 2 ; |
|
|
|
|
||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
4) |
f (x) x4 3x3 10x2 2x 5 , |
|
x 2 . |
|
|
|
|
|||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
193.Используя схему Горнера, найдите частное и остаток от деления многочлена:
1)2x5 3x4 11x3 12x 5 на (x 3) ;
2)8x8 10x7 36x6 28x5 4x3 24x2 20x 11 на (4x 3) .
194.Используя схему Горнера, выполните деление с
остатком в кольцах 2[x] и 5[x] :
1)x3 3x 5 на (x 1) ;
2)2x5 3x3 6x2 7x 2 на (x 2) ;
3) 5x4 3x3 4x2 6x 1 на (x 3) .
45

|
195. Найдите кратность корня x0 |
многочлена f |
[x] : |
|||
1) |
f (x) x5 6x4 11x3 2x2 12x 8 , |
x 2 ; |
|
|||
|
|
|
|
0 |
|
|
2) |
f (x) x5 5x4 7x3 2x2 4x 8 , |
x 2 ; |
|
|||
|
|
|
|
0 |
|
|
3) |
f (x) x5 7x4 16x3 8x2 16x 16 , |
x 2 ; |
|
|||
|
|
|
|
0 |
|
|
4) |
f (x) 3x5 2x4 x3 10x 8 , |
x 1; |
|
|
||
|
|
0 |
|
|
|
|
5) |
f (x) x5 6x4 2x3 36x2 27x 54 , |
x 3 . |
|
|||
|
|
|
|
0 |
|
|
|
196. Может ли кольцо многочленов K[x] |
быть полем? |
||||
|
197. Пусть f , g K[x] и f (x) x4 a , |
g(x) x2 |
bx 1. |
|||
Найдите a и b так, чтобы многочлен |
f (x) делился на g (x) . |
|||||
|
198. Многочлен f [x] четвертой степени со старшим |
|||||
коэффициентом, равным единице, имеет трехкратный корень x0 2 и при делении на (x 3) дает остаток (-1). Найдите
этот многочлен.
199. При каких a, b, c многочлен
f (x) x4 ax3 bx2 cx 1 [x]
имеет корень не ниже второй кратности, равный 1?
|
200. С помощью алгоритма Евклида найдите НОД для |
|||
многочленов f и g над полем |
|
: |
||
1) |
f (x) 2x4 x3 x2 x 3 , |
g(x) x3 2x2 1; |
||
2) |
f (x) x5 2x4 x3 7x2 x 6 , |
g(x) x4 4x3 4x2 3x 14 ; |
||
3) |
f (x) x4 4x3 1, |
g(x) x3 3x2 1 ; |
||
4) |
f (x) x6 x5 3x4 2x3 4x 2 , g(x) x5 3x4 x3 6x2 4x 6 ; |
|||
5) |
f (x) x4 x3 2x2 x 1 , |
g(x) x3 2x2 x 2 ; |
||
6) |
f (x) x4 x3 3x2 4x 1 , |
|
g(x) x3 x2 x 1 ; |
|
7) |
f (x) x4 2x3 2x2 2x 2 , |
g(x) x3 3x 2 ; |
||
8) |
f (x) x6 7x4 8x3 7x 7 , g(x) 3x5 7x3 3x2 7 . |
|||
46

|
201. Найдите НОД и его линейное представление для |
|||||||
многочленов f |
и g над полем |
: |
|
|
|
|||
1) |
f (x) 3x3 2x2 x 2 , |
g(x) x2 x 1 ; |
|
|||||
2) |
f (x) x4 x3 3x2 6x 3 , |
g(x) x3 2x2 2x 1 ; |
||||||
3) |
f (x) x3 1, |
g(x) x4 x3 2x2 x 1 ; |
|
|||||
4) |
f (x) x5 x4 2x3 x2 2x 1 , |
g(x) x4 2x2 x . |
||||||
|
202. Найдите НОД и НОК для многочленов f , g, h [x]: |
|||||||
f (x) x3 2x2 3x 2 , g(x) x4 x3 x2 x 2 , |
h(x) x3 x2 4 . |
|||||||
|
203. Найдите НОД и его линейное представление для |
|||||||
многочленов f |
и g над данным полем |
p : |
|
|||||
1) |
f (x) x5 x4 1, |
g(x) x4 x2 1 , |
p 2 ; |
|||||
2) |
f (x) x5 x3 x 1, |
g(x) x4 1, |
p 2 ; |
|||||
3) |
f (x) x5 x 1 , |
g(x) x4 x3 1, |
p 2 ; |
|||||
4) |
f (x) x5 x3 x , |
g(x) x4 x 1 , |
p 2 ; |
|||||
5) |
f (x) x6 x5 x3 x 2 , g(x) x5 x4 x3 x2 1 , p 3 ; |
|||||||
6) |
f (x) x8 2x5 x3 x2 1 , g(x) 2x6 x5 2x3 2x2 2 , p 3 . |
|||||||
|
204. В каждом из колец |
3[x] , |
5[x] , [x] найдите |
|||||
НОД и НОК для данных многочленов f |
и g : |
|||||||
1) |
f (x) x3 x2 2x 2 , |
|
g(x) x2 x 1 ; |
|
||||
2) |
f (x) x4 x3 x2 1 , |
|
g(x) x3 2x 1; |
|||||
3) |
f (x) x4 2x2 2x 2 , |
g(x) x3 x2 1. |
||||||
205. Постройте унитарные многочлены наименьшей степени над полями и , которые имеют данные корни:
1) 1 - корень кратности два; |
2, 3, |
1 i - простые корни; |
|
2) |
i - корень кратности два; |
1 i |
- простой корень; |
3) |
1 i , 2 i - корни кратности два. |
||
47

|
206. Зная, что многочлен |
f (x) имеет корень c , найдите |
его остальные корни: |
|
|
1) |
f (x) x4 3x3 2x2 x 5 , |
c 2 i ; |
2) |
f (x) x6 9x5 33x4 65x3 74x2 46x 12 , c 1 i . |
|
|
207. Многочлен f [x] |
степени n имеет веществен- |
ный корень кратности n 1. Может ли этот многочлен иметь комплексные корни с ненулевой мнимой частью?
208. |
Найдите канонические разложения |
многочленов |
f ( x) x6 |
1 и g( x) x4 1 над полями , |
, . |
209. Найдите НОД многочленов f (x) и g(x) над полем
,используя разложение на неприводимые множители:
1)f (x) (x 1)81(x 3)4 (x 2)17 ,
g(x) x9 x8 5x7 x6 11x5 13x4 7x3 15x2 4 ;
2) |
f (x) (x3 |
1)(x2 2x 1) , |
g(x) (x2 1)3 ; |
|
3) |
f (x) (x2 x 2)2 (x 1)4 (x 1) , |
|||
|
g(x) (x2 |
x 1)5 (x 2)(x 1)3 ; |
||
4) |
f (x) (x2 |
2x 1)2 (x2 x 1) , |
g(x) (x 2)(x 4)(x 1)2 ; |
|
5) |
f (x) (x2 2x 8)2 (x3 8)(x 2)2 , |
g(x) (3x2 5x 22)2 (x2 16)3 . |
||
|
210. Отделите кратные корни многочлена и напишите |
|||
разложение |
f (x) на неприводимые над полем множители: |
|||
1)f (x) x6 6x4 4x3 9x2 12x 4 ;
2)f (x) x5 8x4 25x3 38x2 28x 8 ;
3)f (x) x6 15x4 8x3 51x2 72x 27 .
211.Докажите, что многочлен второй или третьей степени неприводим над полем P тогда и только тогда, когда он не имеет корней в поле P . Покажите на примере, что уже для многочленов четвертой степени этот факт неверен.
48

212. Докажите, что если многочлен f P[x] взаимно
прост со своей производной, то кратность каждого его неприводимого делителя в каноническом разложении над полем P равна единице.
213. |
Докажите, что если несократимая рациональная дробь |
||||||||
|
m |
является корнем многочлена f (x) a xn a |
|
xn 1 ... a x a |
|||||
|
|
n 1 |
|||||||
|
q |
|
|
|
n |
|
1 0 |
||
|
|
|
|
|
|
|
|
||
с целыми коэффициентами, то: |
|
|
|
|
|||||
|
1) a0 m ; |
2) an q ; |
3) |
f (k) (m kq) |
при любом целом k . |
|
|||
214. |
Докажите, что для любого простого числа p |
мно- |
|||||||
гочлен x p 1 x p 2 |
... x 1 неприводим над полем . |
|
|||||||
215. |
Используя признак Эйзенштейна, докажите непри- |
||||||||
водимость над полем |
следующих многочленов: |
|
|||||||
1) x4 8x3 12x2 6x 2 ; |
2) x5 12x3 36x2 12 ; |
||||||||
3) 6x5 7x4 14x3 28x2 7x 35 ; |
4) xn 5 . |
|
|
||||||
216. |
Установите, какие из следующих многочленов не- |
||||||||
приводимы над полем |
рациональных чисел: |
|
|||||||
1) 2x5 6x4 9x2 12 ; |
2) 3x4 4x3 8x 10 ; |
|
|||||||
3) x2 3x 4 ; |
|
4) x3 12 ; |
|
|
|
||||
5) x3 x 2 ; |
|
6) x3 3x 5 ; |
|
|
|||||
7)x4 2x 3.
217.Разложите многочлены на неприводимые над полем множители:
1) |
x3 3x 2 ; |
2) |
x3 x 1; |
3) |
x4 x3 6x2 3x 6 ; |
4) |
x4 3x3 4x2 18x 18 ; |
5) |
x4 x3 11x2 5x 30 ; |
6) |
x4 2x3 13x2 38x 24 ; |
7) |
x5 x4 6x3 14x2 11x 3; |
8) |
x4 4x3 2x2 12x 9 . |
49

218. Найдите все рациональные корни многочленов:
1) |
x3 6x2 15x 14 ; |
2) x4 2x3 8x2 13x 24 ; |
3) 3x5 2x4 2x3 7x2 7x 3 ; |
4) 3x3 5x2 5x 2 ; |
|
5)2x5 6x4 x3 12x2 15x 6 ;
6)24x5 10x4 x3 19x2 5x 6 ;
7)6x4 19x3 7x2 26x 12 ;
8)8x5 2x4 26x3 11x2 11x 6 ;
9)10x4 13x3 15x2 18x 24 ;
10)6x4 17x3 26x2 37x 30 .
219. Найдите каноническое разложение данных многочленов над полем :
1)x3 32 x2 3x 2 ; 2) x5 233 x4 443 x3 433 x2 59x 30 .
220.Найдите все корни и их кратности для многочленов:
1) |
4x6 24x5 29x4 37x3 34x2 |
39x 9 |
над полем |
|
; |
|||
2) |
x7 4x6 |
4x5 |
2x4 4x3 3x2 |
3x 4 |
над полем |
5 |
; |
|
|
|
|
|
|
|
|
|
|
3) |
x6 2x5 |
3x4 |
x3 4x 3 над полем |
7 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
221. Методом перебора найдите все корни данного многочлена и разложите его на неприводимые множители над данным полем P :
1) |
x3 x 1, |
P |
2 |
; |
|
|
|
|
2) x5 x3 x2 1, |
P |
2 |
; |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3) |
x3 2x2 4x 1, |
|
P |
5 |
; |
|
4) x4 x3 x 2 , |
P |
3 |
; |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5) |
x4 3x3 2x2 x 4 , |
|
P |
5 |
; |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6) |
x6 x5 2x4 3x3 2x2 2x 1, |
P |
5 |
; |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7) |
x5 5x4 x3 6x2 6x 4 , |
|
P |
7 |
; |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8) |
x4 2x3 2x 6, |
P |
7 |
. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50
