Учебное пособие 800508

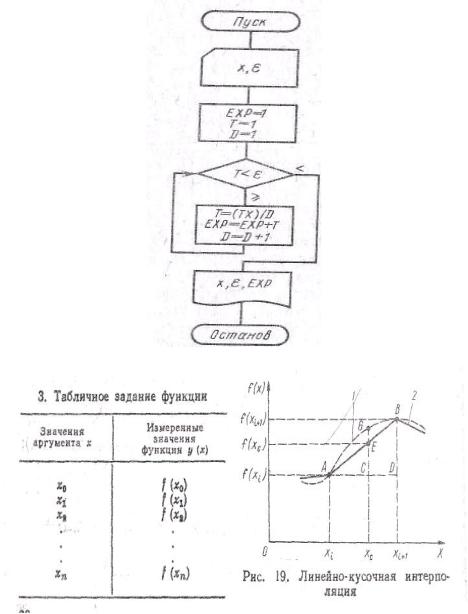
Алгоритм вычисления экспоненциальной функции для заданного в построен по этому принципу приведен на рис. 14. В программе вычисляется последовательно каждый член ряда Т, через его предыдущее значение по рекуррентному соотношению Т = (Тх)/D. К значению ЕХР, полученному на предыдущем шаге, каждый раз добавляется значение следующего члена ряда. Вычисление прекращает

ся как только последующий член ряда станет меньше заданного ε.

Иногда при вычислениях используются непрерывные функции, заданные в виде таблиц, например, полученных в результате эксперимента , как указано в табл. 3, что сделано для того, чтобы в ходе выполнения программы могли вычисляться значения функции в промежуточных точках по отношению к точкам x0, x1… xn , затем производится интерполяция табличной функции.

Наиболее простым является метод линейно-кусочной интерполяции, когда на участках между узлами интерполяции, (x0, x1… xn) функция заменяется линейными отрезками. На рис. 15 ломаная линия 2 получена в результате линейно-кусочной интерполяции, а кривая 1 более точным интерполированием (например, с помощью

вычисления значения функции в точке хc получаем следующую формулу:

Алгоритм линейно-кусочной интерполяции (рис. 16) включает процедуру перебора и сравнения значений табличных аргументов и значения хс. Как только табличное значение аргумента станет больше хс, значит, найден соответствующий отрезок интерполяции, на котором лежит хс.

Рис. 14. Алгоритм для вычисления экспоненциальной функции

Рис. 15. Пример таблицы функций и линейно-кусочной интерполяции

Рис. 16. Алгоритм интерполяции

Более точной является параболическая интерполяция, при которой табличная функция заменяется многочленом θ (х). Степень интерполяционного многочлена не выше п, где п — число узлов интерполяции.

Значения интерполяционного многочлена θ (х) в узлах интерполяции совпадают с табличными значениями функции f (х). Используют различные виды интерполяционных многочленов: Лагранжа, Гаусса, Эрмита, Стирлинга и др / 2 /. Наиболее удобен для реализации на ЭВМ интерполяционный многочлен Ньютона

k 1

где y(x0, x1, …, x k ) – разделенные разности.

Для вычисления разделенных разностей используют формулы:

Численное дифференцирование применяют в том случае, когда функция задана таблично или когда выражение для производной имеет сложный вид.

С помощью интерполяционного многочлена Ньютона (6) задача численного дифференцирования сводится к вычислению разделенных разностей :

Используя лишь несколько первых членов, получим приближенное выражение для каждой производной.

При численном интегрировании используют формулы трапеции, средних, Симпсона, Гаусса и т. д. Эти формулы обычно приводят для интегрирования на равномерной сетке.

Функцию, заданную таблично с неравномерно расположенными узлами интерполяции, можно проинтегрировать по формуле трапеций, т. е. при использовании линейно-кусочной интерполяции. Формула трапеций для этого случая будет иметь вид:

Методы решения линейных систем уравнений делятся на прямые и итерационные. Прямые методы позволяют за конечное число операций получить точное решение. Итерационные методы предполагают получение решения с заданной точностью за несколько циклов. Итерационные методы выгодны для систем большого порядка с разреженными матрицами /3/.

Одним из прямых методов является метод исключения Гаусса /2/, который достаточно просто реализуется на ЭВМ. Метод заключается в приведении матрицы системы уравнений к треугольному виду. Затем система уравнений решается обратным ходом. Приведение к треугольному виду осуществляется с помощью эквивалентных преобразований; сложением строк матрицы, умноженных на соответствующие коэффициенты.

Точность вычисления неизвестных переменных методов Гаусса повышается выбором главного элемента (наибольшего в столбце) и перестановкой его на главную диагональ (за счет перестановки строк).

Рассмотрим численные методы решения алгебраических и трансцендентных уравнений. Алгебраическое или трансцендентное уравнение имеет вид

где f(х) — непрерывная функция.

Врезультате решения необходимо определить корни этого уравнения. В основном для конструкторских задач имеют смысл только действительные корни, т. е. точки, где функция f(х) пересекает ось абсцисс. Задача поиска корней у уравнения (7) имеет несколько этапов. Сначала определяется число корней и отрезки, где они расположены. Затем находятся приближенные значения корней и производится их уточнение. Число действительных корней можно определить с помощью теоремы Штурма. Полезно построить график функции f(х), с помощью которого можно найти области расположения корней. Исходя из конструктивных соображений, почти всегда удается существенно сузить область поиска корней. Приближенные значения корней уточняются с помощью итерационных методов. Наиболее эффективными из них, с учетом реализации на ЭВМ, являются методы дихотомии, простой итерации

иметод Ньютона (рис. 17). Для использования этих методов необходимо знать интервал (а, b), на котором находится интересующий нас корень.

Метод дихотомии, или половинного деления (рис. 17, а) обеспечивает поиск значения корня х* с помощью последовательного деления пополам интервала неопределенности (интервал, содержащий корень). После этого полуинтервал, не содержащий корень, отбрасывается, а оставшийся полуинтервал снова делится пополам, и так до тех пор, пока длина последнего полуинтервала не будет меньше погрешности вычисления корня. Критерием выбора полуинтервала является перемена знака функции f(х) на его концах.

Всхеме алгоритма метода половинного деления (рис. 18) показано, что выбор полуинтервала, содержащего корень уравнения f(х), обеспечивается оценкой знака произведения f (X) × f (А), где X

— середина текущего интервала; A — его левый конец (блок 6). Если это произведение меньше или равно нулю, корень лежит на левом полуинтервале, в противном случае корень лежит на правом

полуинтервале и нужно его взять для последующей процедуры половинного деления.

Рис. 17. Поиск решения методами дихотомии (а), простой итерации (6) и методом Ньютона (в)

Рис. 18. Алгоритм метода половинного деления

Метод половинного деления неприменим для систем алгебраических уравнений, так как имеет небольшую скорость сходимости к точному решению. Этот метод абсолютно устойчив и прост в реализации на ЭВМ.

Метод простой итерации (см. рис. 17, б) ищет решение уравнения (7) как точку пересечения линейной функции у1(х) = х и вспомогательной функции y2 (x). Функция у2(х) строится на базе функции f(х) различными способами. Например, уг (х) = = f (х) + х. В данном случае у2 (х) получается добавлением х к левой и правой частям уравнения (7);

х + f (х) = х или у2 (х) = y1 (х).

Итерация строится на основе нулевого приближения (на рис.

17, б х0 = а). Тогда

x1 =y2 (x0): x2 =y2 (x1):

...................

xn =y2 (xn-1).

Таким образом, в результате первой итерации получаем значение x1 , подставляя его в функцию y2(х), в результате второй итерации получаем приближенное значение корня в виде х2 и т. д. После очередной итерации (см. рис. 17, б) .уточняется значение корня по отношению к его точной величине х*. Метод алгоритмически устойчив, если на отрезке (х0, х1,), | у2' (х) | < 1. Чем меньше | у'2 (х)|, тем быстрее итерации сходятся к х*. ,

Метод простой итерации можно использовать и для системы алгебраических уравнений.

Метод Ньютона, или метод касательных, строится на основе следующей итерационной формулы:

Например, для первой итерации при х0 = а

x1 x0 f (x0 ) . f '(x0 )

Геометрическую интерпретацию для первой итерации можно получить, используя рис. 21, в. Для треугольника Ах0х1 величина х1 - х0 равна высоте f(х0) треугольника, деленной на tg α0; тогда

он сходится лишь в некоторой малой окрестности корня. При реализации на ЭВМ часто используют модифицированный метод Ньютона, при котором производная в знаменателе вычисляется всего один раз, тогда формула (8) примет вид

xn xn 1 f (xn 1 ) . f '(x0 )

Метод Ньютона так же, как и метод простой итерации, применяется для решения систем алгебраических уравнений. Таковы некоторые правила автоматизированных инженерных расчетов с позиции общих методов вычисления.

2.2ИНЖЕНЕРНЫЕ МЕТОДИКИ РАСЧЕТА ДЕТАЛЕЙ

ИУЗЛОВ СТАНКОВ

Процесс получения проектных решений при автоматизации инженерных расчетов в соответствии с принятой математической моделью объекта проектирования ( рис. 9) может быть представлен схемой, приведенной на рис. 19. Инженерная методика расчета, включающая формулу расчета проектных параметров и проверочные расчеты, заложена в виде подпрограммы в памяти ЭВМ. Конструктор вызывает эту подпрограмму и задает в диалоговом режиме исходные

данные (блок 2). К ним в основном относятся значения базовых

~

проектных параметров x1 , значения показателей качества изделия P0

~

и ограничений g 0 . Остальные сведения имеются в банке данных

(блок 5), обслуживающем подпрограмму в виде параметров таблиц и значений аналитических функций.

Далее (блок 3) вычисляются остальные проектные параме-

~

тры x2 , текущие значения показателей качества P1 и ограничений g.

Если условия ограничений и заданные показатели качества выполняются, расчет заканчивается, в противном случае конструктор должен задать в блоке 2 новые исходные данные. Нужно иметь в виду, что часто в роли ограничений используются значения показателей качества.

Общесистемными составляющими функции качества являются критерии точности, устойчивости и эффективности. При расчете деталей станков показатели точности и устойчивости, в основном касаются их геометрии, точнее, сохранения формы под действием различных нагрузок, в первую очередь, силовых, тепловых, изнашивающих. Эффективность выполнения деталями своих функций в станке обеспечивается долговечность оборудования. В свою очередь эта характеристика определяется статической и усталостной прочностью детали.

В основном при расчете станочных узлов и деталей ограничения строятся на базе обеспечения заданной прочности и устойчивости, а показатели качества - на базе параметров, определяющих точность обработки детали на станке. Например, показателем работоспособности несущей системы станка может являться ее жесткость. Детали входят как составные части в станочные узлы, следовательно, для последних сохраняются все те показатели качества, которые имели место для деталей, но в них вкладывается другой смысл.

Одной из основных характеристик деталей являлась их геометрия, а выходной характеристикой узла — перемещение. Например, узлы станков должны обеспечивать точность и устойчивость перемещений, которые они реализуют. Появляются новые оценки эффективности функционирования.

Рис. 19. Схема процесса автоматизированного расчета

Рис. 20. Расчетная схема для определения центра тяжести

станка.

Однако при автоматизированных расчетах используется лишь расчет коэффициентов полезного действия. Точностные показатели и показатели устойчивости используют для оценки детерминированных, установившихся процессов в станочных узлах. Автоматизированные расчеты делятся в зависимости от того, какие инженерные методики реализуют. Так, они могут быть только для вычислений проектных параметров по формулам, только для поверочных расчетов и комбинированные, в этом случае часть проектных параметров рассчитывается, а другая — задается, работоспособность конструкции в целом определяется проверкой. Кроме того, специально, для автоматизированных расчетов могут быть созданы инженерные методики с универсальными математическими моделями.

Даже если автоматизируется готовая инженерная методика, она не может быть целиком, без изменений, внесена в программу расчета. Нужно разработать банк данных, где помещается информация, которую раньше конструктор брал из справочников в виде таблиц, номограмм, графиков, соотношений. Таким образом, требуется провести аппроксимацию данных в виде, удобном для хранения в памяти компьютера. Должны быть решены вопросы эффективного ввода и вывода данных, выдачи сообщений, о неудачно заданных параметрах, режима взаимодействия конструктора и компьютера, максимальной длительности одного цикла решения. Автоматизация инженерных методик позволяет повысить точность расчетов, поэтому могут быть выбраны другие методы вычислений,

Создание современных инженерных методик должно учитывать возможность перевода этой методики на ЭВМ, ибо назначение любых методик является обеспечение сокращения времени вычислений как при ручном, так и при автоматизированном расчете.

Большое количество программ разработано для вычисления исходных данных инженерных методик расчета: моментов инерции, объемов, центра тяжести, площади сечения деталей сложной конфигурации. Представленная на рис. 20 расчетная схема для определения центра тяжести станка предполагает аппроксимацию параллелепипедами отдельных узлов и деталей станка. Для

уточнения расчета можно ввести аппроксимирующие тела типа цилиндра. Центр тяжести (х0, у0, z0,) системы из n-материальных точек можно подсчитать по формулам

где mi — масса i-й точки; xi , yi , zi - координаты центра тяжести i-й точки.

Выражения для координат х0, у9, z9 преобразуем с учетом аппроксимации составных частей станка в виде параллелепипедов; в

i 1

Алгоритм расчета центра тяжести станка показан на рис. 21. Точность полученных координат центра тяжести будет зависеть от степени детализации расчетной схемы станка.

Оценка координат центра тяжести станка на этапе проектирования позволяет предусмотреть конструктивные мероприятия, обеспечивающие удобное и надежное транспортирование станка.

В основном программы чисто вычислительного характера входят фрагментами в программы автоматизированных расчетов, построенных по схеме, приведенной на рис. 22. Рассмотрим примеры алгоритмов таких программ для расчета пружинной подвески вибрационного загрузочного устройства и параметров передачи винт—гайка качения.

Вибрационное загрузочное устройство (ВЗУ) состоит из основания 5 (рис. 26, а), амортизаторов 6, электромагнита 4, установ ленного под углом, пружинных подвесок / и лотка 3 с деталью При

Вычисляется наибольшая осевая нагрузка [Q]H при максимальном и номинальном натяге (блок 7). Эта нагрузка не должна превышать 0,9 [Q]. Рассчитывают податливости передачи δ', δ", угол

трения ρ и относительные значения сил (Q1)', (Q1)", где Q1 Q1 / PH .

Далее при неавтоматизированном расчете по графику (рис. 30) определяют относительные усилия.

Для аналитического расчета PI и PII необходимо решить эти нелинейные алгебраические уравнения. В блоке 11 расчет PI и PII производится методом половинного деления.

Расчет заканчивается вычислением коэффициента полезного действия передачи η, наименьшей нагрузки QT, начиная с которой

передача перестает быть самотормозящей, и момента вспомогательного (холостого) хода Мx. Результаты расчета выводятся на экран дисплея (блок 13) и анализируются. Если какие-то параметры передачи не удовлетворяют заданным требованиям, расчет повторяется при других исходных данных.

2.3 АВТОМАТИЗИРОВАННЫЙ РАСЧЕТ ДЕТАЛЕЙ И УЗЛОВ СТАНКОВ ПО УНИВЕРСАЛЬНЫМ

МАТЕМАТИЧЕСКИМ МОДЕЛЯМ

Одним из основных требований, предъявляемых к математическим моделям автоматизированного проектирования, является их универсальность. Это означает, что если обычно для расчета однотипных механизмов создаются отдельные программы, то

привести обобщенную математическую модель к виду, который

моделей различают в зависимости от того, к какой расчетной схеме приводится объект: к расчетной схеме детали или к расчетной схеме узла (как совокупности отдельных элементов и устройств). Особенности этих методов рассмотрим на двух примерах. В качестве первого будет автоматизированный расчет много пролетных балок, в качестве второго — расчетная модель станочного гидропривода. В первом примере расчет станочных узлов сводится к расчету детали (многопролетной балки); во втором случае рассчитывают систему, состоящую из отдельных гидравлических устройств и элементов.