
Учебное пособие 800306
.pdf
д) в разделе Distance measure выберите Squared Euclidean distances (квадрат евклидовой метрики) и нажмите ОК.
В появившемся окне нажмите на кнопку Vertical icicle plot. На экране появится дендрограмма (рис. 18), показывающая объединение объектов, расстояние между которыми является наименьшим, в кластеры.
Рис. 18. Дендрограмма при методе одиночной связи
На вертикальной оси дендрограммы откладываются расстояния между объектами и между объектами и кластерами. Так, расстояние между объектами С, и С2 равно 5 (см. матрицу расстояний D2 , в примере 1). Эти объекты объединяются в
один кластер на первом шаге.
Расстояние между этим кластером и объектом С3 равно 8 (см. матрицу расстояний D2 ). Объект С3 объединяется с
кластером (С1, С2) на втором шаге. Наконец, расстояние между объектом С4 и кластером (С1, С2, С3) равно 13 (см. матрицу расстояний D3 ).
Таким образом, горизонтальные отрезки дендрограммы проводятся на уровнях, соответствующих пороговым значениям расстояний, выбираемым для данного шага кластеризации.
Кластеризация методом одиночной связи (ближайшего соседа) приводит к образованию одного кластера (пороговое
29

расстояние равно 13).
Далее последовательно нажмите Continue... и Cancel и в окне установок процедуры в разделе Amalgamation... выберите Complete Linkage. После выполнения процедуры появится следующая дендрограмма (рис. 19).
Рис. 19. Дендрограмма при методе полной связи
Вторая дендрогамма показывает, что кластеризация методом полной связи (дальнего соседа) при таком же пороговом расстоянии равным 13, приводит к образованию двух кластеров. Сравните полученные дендрограммы с результатами решения примера 1.
Задания для самостоятельного решения
1.Используя иерархические алгоритмы, проведите кластеризацию данных из примера 2. Сравните результаты с результатами в примере 2.
2.На предприятии существует 16 научнопроизводственных отделов, занятых выпуском различной продукции, работ, услуг. Поскольку виды деятельности, количество работающих, рентабельность отделов, существенно различаются между собой, было решено сгруппировать отделы
внесколько однородных групп, а затем для каждой группы разработать свою систему премирования.
30

После тщательного анализа выбрали четыре признака, с помощью которых описывались важные (для указанной цели)
параметры каждого отдела: X1 |
– стоимость активной части ос- |
||||||||||
новных |
производственных |
фондов, тыс. руб.; X 2 |
– средне- |
||||||||
месячный объем работ отдела, тыс. руб.; X 3 |
– удельный вес |
||||||||||
работ/услуг отдела по внутрифирменной кооперации, %; |
X 4 – |
||||||||||
среднемесячная прибыль отдела, тыс. руб. |
|
|
|
||||||||
Исходные данные по отделам приведены ниже (табл. 9). |
|||||||||||
|
|
|
|
|
|
|
|
|
|
Таблица 9 |
|
|
|
|
Исходные данные по отделам |
|
|
|
|||||
№ |
|
Значения признаков |
|
№ |
Значения признаков |
||||||
отдела |
|
|
|
|
|
|
отдела |
|
|
|
|
|
X1 |
X 2 |
X 3 |
X 4 |
|
X1 |
X 2 |
X 3 |
X 4 |
||
|
|
|
|
||||||||
1 |
|
699 |
190 |
53 |
11 |
|
9 |
293 |
391 |
16 |
66 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
532 |
211 |
19 |
42 |
|
10 |
300 |
396 |
29 |
87 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
650 |
152 |
46 |
14 |
|
11 |
73 |
160 |
0 |
22 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
768 |
216 |
67 |
17 |
|
12 |
862 |
199 |
51 |
22 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
67 |
106 |
0 |
32 |
|
13 |
112 |
136 |
0 |
29 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
322 |
397 |
26 |
52 |
|
14 |
289 |
388 |
31 |
74 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
736 |
180 |
49 |
18 |
|
15 |
512 |
195 |
6 |
58 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
501 |
239 |
11 |
60 |
|
16 |
490 |
201 |
9 |
65 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проведите |
кластеризацию |
отделов |
используя |
|||||||
иерархические алгоритмы (Joining): |
|
|
|
|
||||||||
|
|
а) |
|
используя исходные данные; |
|
|
||||||
|
|
б) |
|
используя стандартизованные данные, т. е. данные, |
||||||||
преобразованные по формуле |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X ij |
X j |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
S j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где X ij |
i |
е значение j го признака, i |
1,2,...,16; j |
1,2,3,4; |
||||||||
|
|
|
1 |
16 |
оценка среднего для |
j го признака; |
||||||
|
|
|
||||||||||
|
X j |
|
|
|
xij |
|||||||
|
|
|
|
|||||||||
|
|
|
16 i 1 |
|
|
|
|
|
|
|||
31
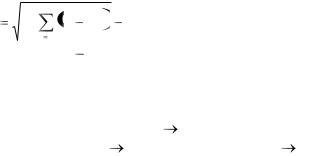
|
1 |
16 |
|
|
|
2 |
оценка |
среднего квадратического |
||
S j |
xij |
x j |
||||||||
|
|
|
|
|||||||
15 i 1 |
|
|||||||||
отклонения для |
j |
го признака. |
|
|||||||
|
Процедуру стандартизации |
данных можно выполнить |
||||||||
непосредственно в таблице, используя следующую последовательность действий: курсор на имени переменной 
нажать правую кнопку мыши |
в выпадающем меню выбрать |
||
File/Standardize Block |
Standardize Columns |
ОК. |
|
Сравните результаты |
кластеризации. |
По результатам |
|
кластеризации определите число кластеров и их состав. Найдите статистические характеристики каждого кластера.
Проведите кластеризацию используя метод К-средних (число кластеров задайте равным 4). Сравните результаты (составы кластеров).
3.4. Общие положения разомкнутых сетей массового обслуживания
1. Постановка задачи по разомкнутой сети Джексона
Первой работой, посвященной разомкнутым сетям массового обслуживания (РСеМО), является работа Дж. Р. Джексона, опубликованная в 1957 г. С тех пор произошло существенное расширение спектра изучаемых СеМО как достаточно адекватных моделей реальных сложных информационных, производственных, вычислительных, связевых и т.п. систем и сетей, используемых в самых разнообразных областях человеческой деятельности. При этом учитывались многие особенности функционирования реальных систем и сетей. Большинство результатов получено для стационарного режима.
Для теории и практики непосредственный интерес представляет получение результатов для нестационарного режима. Для этого режима точные результаты по РСеМО получены только для частного случая РСеМО Джексона. Для лучшего понимания последующих результатов для нестационарного режима марковских СеМО и их места в общей теории СеМО целесообразно привести с
32

доказательствами точные результаты для РСеМО Джексона по [3]. Сначала приведем постановку задачи.
Постановка задачи. Сеть состоит из т перенумерованных узлов. На вход сети поступает пуассоновский поток однородных требований интенсивности . Поступившее требование с вероятностью P0i поступает на обслуживание в i -
m
ый узел, P0i 1. Длительность обслуживания в i -ом узле
i 1
является случайной величиной, имеющей экспоненциальное распределение с пара-метром, зависящим от числа требований в узле. Более точно, если в момент t в i -ом узле имеется l требований, то в интервале t,t dt , где dt мало, закончится обслуживание одного требования с вероятностью
i l dt o dt ,0 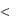 i l
i l ,l 1,2,...,
,l 1,2,...,
или закончится время пребывания одного требования в узле с вероятностью
|
|
vi |
l dt |
o dt ,0 |
vi l |
,l |
1,2,... |
|
||
|
Далее и в том, и в другом случае это требование |
|||||||||
мгновенно поступает на обслуживание в |
j -ый узел с |
|||||||||
вероятностью |
Pij |
и с |
вероятностью |
Pi0 |
покидает |
сеть, |
||||
m |
|
|
|
|
|
|
|
|
|
|
Pij |
Pio 1,i |
1,...,m . Матрица |
Pij |
m m |
неразложима. |
|
||||
j 1 |
|
|
|
|
|
|
|
|
|
|
|
Вводится случайный процесс |
|
|
|
|
|||||
|
|
|
|
v t |
v1 t ,...,vm t , |
|
|
|||
где vi |
t — число требований в i -ом узле в момент t, i |
1,...,m . |
||||||||
В силу предпосылок постановки задачи он является марковским случайным процессом. Обозначим
P k1,...,km ,t |
P v1 t k1,...,vm t |
km , |
Требуется определить |
нестационарное |
распределение |
вероятностей состояний этой сети P k1,...,km ,t .
В практических задачах используются, как правило, не нестационарные распределения вероятностей состояний сети, а
33
функционалы от них, обычно начальные, смешанные и центральные моменты, корреляционные функции, взаимно корреляционные функции, которые являются характеристиками сети. С этих позиций в последующих главах этой части осуществляется развитие точных методов определения этих нестационарных характеристик РСеМО – вышеуказанных функционалов от нестационарных распределений вероятностей состояний разомкнутых сетей массового обслуживания,
при произвольных начальных условиях и постоянных параметрах РСеМО в следующих направлениях:
1. Нахождение явного аналитического вида нестационарных математических ожиданий количества требований в узлах.
Итак, вместо решения бесконечной системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами разрабатывается метод нахождения для нестационарных математических ожиданий количества требований в узлах системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами порядка, равного числу узлов в сети, на базе метода стохастических разностных уравнений. Для решения этой системы уравнений будет использовано преобразование Лапласа с последующим его обращением и получением явного аналитического вида для искомых нестационарных математических ожиданий. Обращение преобразование Лапласа будет проводиться с использованием операции определения корней полинома т-ой степени, где m количество узлов в сети.
Заметим, что из теоремы 2.1 следуют уравнения для нестационарных математических ожиданий, но только в случае, когда начальные условия не являются произвольными, а имеют конкретный вид произведения пуассоновских распределений количества требований в узлах. Ставится же задача нахождения нестационарных математических ожиданий для произвольных начальных условий.
2. Нахождение системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами для нестационарных начальных смешанных моментов второго
34
порядка количества требований в узлах. Решение этой системы с получением явного аналитического вида при использовании преобразования Лапласа и последующим определением корней
полинома степени C 3 |
и его обращением полностью |
m |
|
аналогично вышеуказанному решению системы уравнений для нестационарных математических ожиданий количества требований в узлах сети кроме одного обстоятельства. Это обстоятельство состоит в том, что решение выражается через нестационарные математические ожидания количества требований в узлах сети в виде рекуррентных формул.
3.Нахождение системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами для нестационарных начальных и смешанных моментов произвольного порядка количества требований в узлах. Решение этой системы с получением явного аналитического вида при использовании преобразования Лапласа и последующим определением корней полинома и его обращением, конечно, значительно более громоздко вследствие существенного возрастания размерности системы уравнений, но, по существу, полностью аналогично вышеуказанному решению системы уравнений для нестационарных математических ожиданий количества требований в узлах сети за исключением также одного обстоятельства. Здесь это обстоятельство состоит в том, что решение выражается через нестационарные начальные и смешанные моменты количества требований в узлах сети порядка, на 1 меньшего, в виде рекуррентных формул.
Далее движение по этим рекуррентным формулам приводит к выражению искомых моментов через нестационарные математические ожидания количества требований в узлах сети, для которых решается в виде, указанном в пункте 1.
4.Далее производится обобщение на разные классы требований и т. д.
Осуществляется также развитие итерационных методов определения вышеуказанных функционалов от нестационарных распределений вероятностей состояний разомкнутых сетей
35
массового обслуживания при произвольных начальных условиях
и параметрах РСеМО, зависящих от времени и нестационарных начальных и смешанных моментов, в тех же направлениях.
Задачи определения нестационарных моментов для разомкнутой сети массового обслуживания
Для разомкнутых сетей массового обслуживания (РСеМО) с экспоненциально распределенными длительностями обслуживания и входящим пуассоновским потоком получение искомых вероятностных характеристик производится из вероятностей состояний, для которых в нестационарном случае составляются системы линейных дифференциальных уравнений первого порядка. Находя вероятности состояний из этих уравнений, далее определяются искомые вероятностные характеристики, в частности, математические ожидания количества требований в узлах РСеМО и другие моменты. Размерность систем линейных дифференциальных уравнений первого порядка для вероятностей состояний для РСеМО, как правило, весьма велика, как указывалось выше, во многих случаях она равна бесконечности.
Получение численных, а тем более аналитических, решений систем линейных дифференциальных уравнений первого порядка для вероятностей состояний в нестационарном случае при указанных выше размерностях уже представляет проблему.
Если нас интересуют математические ожидания количества требований в узлах СеМО в нестационарном случае и при этом можно было бы составлять уравнения непосредственно для них, то в этом случае было бы всего т уравнений. Здесь, как и в общем случае, возникают две задачи.
Первая задача: выяснить условия, при которых можно составлять системы линейных дифференциальных уравнений первого порядка сразу для математических ожиданий количества требований в узлах РСеМО, причем в эти уравнения не должны входить вероятности отдельных состояний, а также для других моментов (начальных, центральных) и для других характеристик этих количеств, если
36
можно. Как указывалось выше, условие, чтобы в системы линейных дифференциальных уравнений первого порядка для математических ожиданий не входили вероятности отдельных состояний, существенно, ибо для нахождения их надо решать исходную систему линейных дифференциальных уравнений первого порядка для всех вероятностей состояний.
Вторая задача: при выполнении условий задачи 1 предложить и обосновать способ составления системы линейных дифференциальных уравнений первого порядка сразу для нестационарных математических ожиданий количества требований в узлах РСеМО, в которые бы не входили вероятности отдельных состояний.
Примеры определения нестационарных моментов для разомкнутой сети массового обслуживания
Для того чтобы понять специфику проблемы определения нестационарных моментов для РСеМО, приведем несколько примеров.
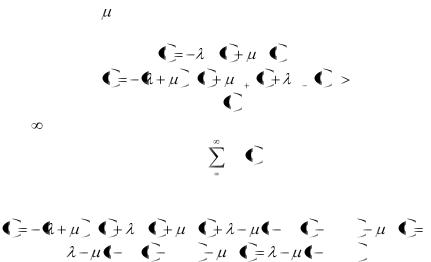
Пример 1. Рассмотрим систему М/М/1 с интенсивностью входящего пуассоновского потока  и интенсивностью обслуживания . Для вероятностей состояний имеем следующую систему дифференциальных уравнений:
и интенсивностью обслуживания . Для вероятностей состояний имеем следующую систему дифференциальных уравнений:
P' t |
P |
t |
|
P t , |
|
(1) |
0 |
0 |
|
|
1 |
|
|
P' t |
P t |
P |
1 |
t |
P |
t ,t 0. |
i |
i |
i |
|
i 1 |
|
|
Умножим уравнение для Pi |
t на i и просуммируем по i |
|||||
от 1 до . |
|
|
|
|
|
|
Тогда имеем (обозначим |
iPi |
t |
через m(t)) следующее |
|||
|
i 1 |
|
|
|
|
|
уравнение для математического ожидания количества требований в системе в нестационарном случае
m' t |
m t m t m t |
1 P t P (t) |
P t |
|
|
|
0 |
1 |
1 |
= |
1 P t |
P (t) |
P t |
1 P (t) . |
(2) |
|
0 |
1 |
1 |
0 |
|
37

(В стационарном случае m'(t) = 0 и из этого уравнения
вытекает известное равенство P0 1 |
|
). |
|
Как видно из полученного уравнения, в него входит вероятность P0(t), т.е. в этом случае не удовлетворяется требование задачи 1.
Пример 2. Рассмотрим разомкнутую СеМО с двумя узлами с потерями. Входящий поток является пуассоновским с параметром . Поступающее требование с вероятностью Pi
поступает на i-ый узел, i = 1,2. Длительность обслуживания в обоих узлах имеет экспоненциальные распределения с параметрами 1 , и 2 соответственно. Система дифферен-
циальных уравнений для вероятностей состояний для этой СеМО имеет вид
|
|
P' |
t |
|
|
|
|
P |
|
|
t |
|
|
|
1 |
P |
|
t |
2 |
P |
|
|
t |
, |
|
|||
|
|
00 |
|
|
|
|
00 |
|
|
|
|
|
10 |
|
|
|
01 |
|
|
|
|
|||||||
|
P' t |
|
|
|
p |
2 |
|
|
1 |
P t |
|
|
|
|
2 |
P t |
|
|
|
p P t , |
||||||||
|
10 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
11 |
|
|
|
|
|
1 |
00 |
|
|||||
P' |
t |
p |
|
2 |
P |
|
t |
|
|
|
1 |
P |
|
t |
|
|
p |
P |
|
t , |
(3) |
|||||||
01 |
|
|
1 |
|
|
01 |
|
|
|
|
|
11 |
|
|
|
2 |
|
00 |
|
|
|
|
||||||
|
P' |
|
|
|
1 |
|
|
2 |
P t |
|
|
|
p P t |
|
|
p |
|
P t . |
||||||||||
|
11 |
|
|
|
|
|
|
11 |
|
|
|
|
|
|
1 |
01 |
|
|
|
2 |
|
10 |
|
|||||
Обозначим |
через |
|
|
mi |
t |
|
|
математическое |
ожидание |
|||||||||||||||||||
количества |
требований |
|
в |
|
i |
|
|
узле, |
|
|
i |
1,2 . |
|
|
Для |
m1 t по |
||||||||||||
определению имеем |
m t |
|
|
P |
|
|
t |
|
P |
|
t . |
Тогда |
из |
системы |
||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
10 |
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
||
уравнений (3) для m1 |
t получаем дифференциальное уравнение |
|||||||||||||||||||||||||||
|
m' |
t |
|
|
|
1 |
m |
|
t |
|
|
|
p |
|
P |
|
t |
P |
|
t |
|
|
(4) |
|||||
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
01 |
|
|
00 |
|
|
|
|
|
|||||
Для |
m2 t |
|
из |
|
системы |
|
уравнений |
|
|
(3) |
получаем |
|||||||||||||||||
дифференциальное уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
m' t |
|
|
2 |
m |
|
t |
|
|
|
p |
2 |
P (t) |
|
P (t) |
|
|
|
|
|
(5) |
|||||||
|
2 |
|
|
2 |
|
|
|
|
|
|
10 |
|
|
|
|
00 |
|
|
|
|
|
|
|
|||||
Как видно из полученных уравнений, в них входит |
||||||||||||||||||||||||||||
вероятность |
P00 t |
другие вероятности, |
т.е. и в этом случае не |
|||||||||||||||||||||||||
удовлетворяется требование задачи 1.
Таким образом, можно сделать следующие выводы:
- наличие очередей в СМО, которое имеет место в
38
