
Теория функций комплексного переменного и операционное исчисление. Бондарев А.В., Ряжских А.В
.pdf
6.ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Вэтой главе мы рассмотрим определение и основные свойства преобразования Лапласа, на базе которого будет строиться операционное исчисление.
Операционное исчисление – один из методов математического анализа, позволяющий в ряде случаев сводить исследование дифференциальных и некоторых типов интегральных операторов и решение уравнений, содержащих эти операторы,
крешению более простых алгебраических задач. Решение задачи операционным методом осуществляется по следующей схеме:
1. От искомых функций переходят к некоторым другим функциям – их изображениям.
2. Над изображениями производят операции, соответствующие заданным операциям над самими функциями.
3. Произведя действия над изображениями и получив некоторый результат, возвращаются к самим функциям.
Вкачестве преобразования, позволяющего перейти от функций к их изображениям, будем применять преобразование Лапласа.
6.1. Оригиналы и их изображения
Пусть f t – действительная функция действительного переменного t. Функция f t называется оригиналом, если она удовлетворяет следующим условиям:
1.f t 0 при t 0 .
2.Функция f t кусочно-непрерывная при t 0 , т.е она
непрерывна или имеет точки разрыва первого рода, причем на каждом конечном отрезке таких точек конечное число.
3. Существуют такие числа M 0 и 0, что для всех t выполняется неравенство f t Me t , т.е. при возрастании t
71
функция f t может возрастать не быстрее некоторой показательной функции. Число называется порядком роста функции f t .
Первое условие означает, что некоторый физический процесс, описываемый функцией f t , начинается с некото-
рого момента времени (удобнее считать, что в момент t 0 ). Третьему условию удовлетворяют ограниченные функции (в
частности, sin t и cos t ), степенные t n ( n 0 ), показательные eat и другие. В качестве примера функции, для которой условие 3 не выполняется, можно указать eat2 . Не является ориги-
налом также функция |
|
1 |
, т.к. она не удовлетворяет условию 2. |
||||
|
|||||||
|
f t |
|
t |
|
|
|
|
Функция |
может быть и комплексной функцией |
||||||
действительного |
переменного, |
т.е. |
иметь |
вид |
|||
f t f1 t i |
f2 t . Она является оригиналом, если действи- |
||||||
тельные функции f1 t и f2 t – оригиналы.
Преобразованием Лапласа, или изображением оригинала
f t |
называется функция |
F p комплексного переменного |
||||
p i , определяемая формулой |
|
|
|
|||
|
|
|
|
|
|
|
|
|
F p f t e pt dt . |
|
(6.1) |
||
|
|
|
0 |
|
|
|
Соответствие между оригиналом |
f t и изображением |
|||||
F p |
записывается в виде |
F p =∙ f |
t , |
f t |
=∙ F p или |
|
|
|
|
∙ |
|
|
∙ |
F p |
L f |
t . |
|
|
|
|
|
|
|
|
|
|
|
Теорема. Для всякого оригинала |
f t |
изображение |
||||
F p |
существует в полуплоскости Re p 0 , где 0 – по- |
|||||
рядок роста функции f t , |
причем функция |
F p является |
||||
72
аналитической в этой полуплоскости. |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
Докажем первую часть теоремы. Пусть |
p i – про- |
||||||||||||||||||
извольная точка полуплоскости Re p 0 |
. Учитывая, что |
||||||||||||||||||||||
|
|
f t |
|
Me 0t , находим: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
f t e pt dt |
|
|
f t e pt |
|
dt M e 0t |
|
e pt |
|
|
dt M e 0t e t dt |
|||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
0 |
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
M e 0 t dt |
|
|
. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
F p |
|
|
f t e pt dt |
|
|
. |
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
0 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Отсюда вытекает абсолютная сходимость интеграла (6.1), т.е. изображение F p существует и однозначно в полуплоскости
Re p 0 .
Следствие. Если функция F p является изображением
функции f t , то lim F p 0 . Отсюда, в частности, следует,
p
что функции F p 5 или F p p2 не могут быть изобра-
жениями.
Пример 1. Найти изображение единичной функции Хеви-
1 |
при t 0 |
|
сайда t |
|
(рис. 6.1). |
0 при t<0 |
|
|
73
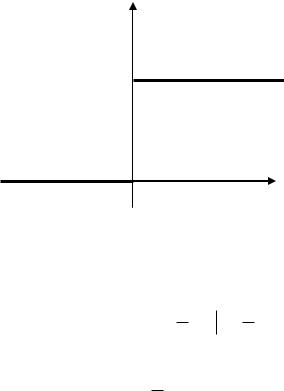
(t)
1
O
Рис. 6.1.
По формуле (6.1) находим
F p 1 e pt dt 1p e pt
0
Таким образом,
1 ∙=∙ 1p .
t
1 .
0 p
(6.2)
В операционном исчислении функцию-оригинал кратко записывают в виде f t , подразумевая, что
f |
t |
при t 0 |
|
|
|
|
|
f t |
|
при t<0 |
. |
0 |
|
|
|
|
|
|
|
Пример 2. Найти изображение функции f t eat , где a
– постоянное комплексное или действительное число. Тогда
|
|
1 |
|
|
|
1 |
|
|
F p eat e pt dt e p a t dt |
e p a t |
|
|
|
||||
|
|
|||||||
|
|
|
|
|
, |
|||
p a |
|
0 |
p a |
|||||
|
|
|
||||||
0 |
0 |
|
|
|
|
|
|
|
если Re p a 0, т.е. Re p Re a . Таким образом,
74
|
|
|
eat |
∙=∙ |
|
|
1 |
. |
|
|
|
|
(6.3) |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
p a |
|
|
|
|
||||||
6.2. Свойства преобразования Лапласа |
|
|
|
|||||||||||
6.2.1. Линейность |
|
|
|
|
|
|
|
|
|
|
|
|
||
Если f1 t |
∙=∙ F1 p , |
f2 t |
∙=∙ F2 p , |
c1 |
и c2 |
– постоян- |
||||||||
ные числа, то |
|
|
|
|
|
=∙ c F |
|
|
|
|
|
|||
c |
f |
t c |
f |
2 |
t |
p c F |
p , |
(6.4) |
||||||
1 |
1 |
2 |
|
|
∙ |
1 1 |
|
2 |
2 |
|
|
|||
т.е. линейной комбинации оригиналов соответствует такая же линейная комбинация изображений.
Доказательство. Используя свойства интеграла, находим:
|
|
|
|
|
|
|
|
|
|
|
|
c f |
t c f |
|
t e pt dt c |
|
f |
t e pt dt c |
2 |
f |
|
t e pt dt |
|
1 1 |
2 |
2 |
|
1 |
1 |
|
|
2 |
|
||
0 |
|
|
|
|
0 |
|
|
0 |
|
|
|
c1 F1 p c2 F2 p .
Пример. Найти изображения функций sin t , cos t , sh t , ch t .
Пользуясь свойством линейности и формулой (6.3), находим:
sin t |
ei t e i t |
=∙ |
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
2i |
∙ |
2i p i |
|
|
|
|
|
p i |
|
|
|
p2 |
2 |
|
||||||||||||||||||||||
|
|
ei t e i t |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
||||||||||
cos t |
|
|
|
|
=∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
|
∙ |
2 |
p i |
|
|
|
|
|
p i |
|
|
|
|
p2 |
2 |
|
||||||||||||||||||||
|
|
|
e t e t |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
sh t |
|
|
|
=∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
|
||||||||||||||||||||||
|
|
2 |
|
∙ |
2 |
|
|
p |
|
|
|
|
|
|
p |
|
|
2 |
|
|
|
|
|||||||||||||||||
|
|
|
e t e t |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
p |
|
|
|
|
|
||||||||||
ch t |
|
|
|
=∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 2 |
|
|
|
|||||||||||||||||||||||
|
|
2 |
|
∙ |
2 |
|
p |
|
|
|
|
|
|
p |
|
|
|
|
|
|
|||||||||||||||||||
Таким образом,
75

sin t
cos t
sh t
ch t
∙=∙ ∙=∙ ∙=∙ ∙=∙
|
|
, |
(6.5) |
|||
p2 2 |
||||||
|
p |
|
, |
(6.6) |
||
|
|
|
|
|||
|
p2 2 |
|
||||
|
|
, |
(6.7) |
|||
|
|
|
||||
|
p2 2 |
|||||
|
p |
|
|
. |
(6.8) |
|
|
|
|||||
|
p2 2 |
|||||
6.2.2. Подобие
Если f t ∙=∙ F p , то для любого постоянного 0
f t |
|
∙ 1 |
|
p |
|
|
||
= |
|
F |
|
|
, |
(6.9) |
||
|
|
|||||||
|
∙ |
|
|
|
|
|
|
|
т.е. умножение аргумента оригинала на положительное числоприводит к делению изображения и его аргумента на это число.
Доказательство. По формуле (6.1) имеем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f t ∙=∙ f t e pt dt . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сделаем в этом интеграле подстановку |
t t |
, |
dt |
|
1 |
dt |
. То- |
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
гда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
p |
t1 |
|
|
|
|
|
1 |
|
|
|
p |
t |
|
|
|
1 |
|
|
p |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
f t ∙=∙ |
|
f t1 e |
dt1 |
|
f |
t e |
dt |
|
|
F |
|
|
|
. |
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
o |
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример. Зная, что sin t |
∙=∙ |
|
|
1 |
|
, находим |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
p2 1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
sin t |
∙=∙ |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
p |
2 |
|
|
p2 |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
76
6.2.3. Теорема о смещении изображения |
|
|||||||||
Если f t ∙=∙ |
F p , a const , то |
|
|
|
||||||
|
|
eat f t =∙ F p a , |
|
|
(6.10) |
|||||
|
|
|
∙ |
|
|
|
|
|
|
|
т.е. умножение оригинала на функцию eat |
|
соответствует сме- |
||||||||
щению переменной p. |
|
|
|
|
|
|
|
|
||
Доказательство. По формуле (6.1) имеем |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
eat f t ∙=∙ eat f t e pt dt f t e p a t dt F p a . |
||||||||||
0 |
|
|
|
0 |
|
|
|
|
||
Из формулы (6.10) следует, что |
|
|
|
|
||||||
eat sin t ∙=∙ |
|
|
|
|
, |
(6.11) |
||||
|
|
|
|
|||||||
|
p a 2 |
2 |
||||||||
e |
at |
cos t ∙=∙ |
|
|
p a |
, |
(6.12) |
|||
|
|
p a 2 |
2 |
|||||||
|
eat |
sh t ∙=∙ |
|
|
|
|
|
, |
(6.13) |
|
|
|
|
|
|
|
|||||
|
|
|
p a 2 |
2 |
|
|||||
|
e |
at |
ch t ∙=∙ |
|
|
p a |
|
, |
(6.14) |
|
|
|
|
|
p a 2 |
2 |
|
||||
6.2.4. Запаздывание |
|
|
|
|
|
|
|
|||
Если f t =∙ |
F p , a 0 , то |
|
|
|
|
|||||
∙ |
|
|
f t a |
=∙ e ap F p , |
|
|
|
|||
|
|
|
|
|
(6.15) |
|||||
|
|
|
|
∙ |
|
|
|
|
||
т.е. запаздывание оригинала на положительную величину a
приводит к умножению изображения на e ap . Доказательство. По формуле (6.1) имеем
|
|
f t a ∙=∙ f t a e pt dt f t1 e p t1 a dt1 |
|
0 |
a |
77

|
|
|
|
|
|
|
|
|
|
|
|
|
|
f t1 e ape pt1 dt1 e ap f t e pt dt e ap F p . |
|
||||||||||||
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
6.2.5. Дифференцирование оригинала |
|
||||||||||||
Если |
f t |
|
∙=∙ F p |
и функции |
f t , |
f t , …, |
f n t |
||||||
являются оригиналами, то |
|
|
|
|
|
|
|||||||
|
|
|
|
|
f t ∙=∙ p F p f 0 , |
|
|
(6.16) |
|||||
|
|
f t ∙=∙ p2 F p p f 0 f 0 , |
(6.17) |
||||||||||
|
|
……………………………………... |
|
||||||||||
|
f |
n t |
=∙ pn F p pn 1 f 0 ... f n 1 0 . |
(6.18) |
|||||||||
|
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
Доказательство. По определению изображения находим: |
|||||||||||||
|
|
|
|
|
|
|
|
|
u e pt |
du pe pt dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
∙ |
|
|
|
pt |
|
|
|
|
|||
f t |
∙= f t e |
dt |
|
dv f t dt |
v f t |
|
|
||||||
|
|
||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f t e pt p f t e pt dt f 0 p F p .
0
0
Пользуясь полученным результатом, найдем изображение второй производной f t :
f t f t ∙=∙ p p F p f 0 f 0p2 F p p f 0 f 0 .
Применяя формулу (6.16) (n–1) раз, получим формулу (6.18).
6.2.6. Дифференцирование изображения |
|
Если f t =∙ F p , то |
|
∙ |
|
t f t ∙=∙ F p , |
t n f t ∙=∙ F n p , (6.19) |
т.е. дифференцированию изображения по переменной p соответствует умножение оригинала на t .
Доказательство. Т.к. функция F(p) аналитична в полу-
78
плоскости Re p 0 , то в каждой точке этой полуплоско-
сти функция F(p) имеет производные любого порядка. Поэтому
|
F |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t f t e |
|
|
|
dt ∙= |
t f t . |
|
|||||||||||||||||||
|
f t e |
|
p dt |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pt |
|
|
∙ |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Применяя это правило n раз, получим t n f |
t ∙=∙ F n p . |
|
||||||||||||||||||||||||||||||||||||||||||
Пример. Пусть |
f t 1 n . Так как 1 n ∙=∙ 1 n |
, то |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n |
|
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n! |
|
|||||
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
t |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
n |
|
|
|
|
|
|
||||||||||||||
|
|
= |
|
|
|
|
|
|
|
|
... |
|
|
|
. |
|||||||||||||||||||||||||||||
|
|
|
|
1 |
|
∙ |
|
|
p |
|
|
|
1 |
|
|
|
1 |
|
|
|
pn 1 |
|
pn 1 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t n ∙=∙ |
n! |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.20) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pn 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
В частности, t ∙=∙ |
|
|
1 |
|
; |
t2 |
∙=∙ |
2 |
; t3 |
∙=∙ |
6 |
|
и т.д. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
p2 |
|
|
p3 |
|
p4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
6.2.7. Интегрирование оригинала |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
Если |
|
f t |
|
=∙ F p |
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
F p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f d ∙=∙ |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
(6.21) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. интегрированию оригинала в пределах от 0 до t соответствует деление изображения на p.
Доказательство. t
0
t |
|
|
|
|||
∙ |
|
|
|
pt |
|
|
f d ∙= |
f d |
e |
dt. Приме- |
|||
|
||||||
0 |
|
0 |
|
|
|
|
ним для вычисления этого интеграла формулу интегрирования
79

t |
|
|
1 |
|
||
по частям: u f d , |
dv e pt dt , |
du f t dt , |
e pt . |
|||
v |
|
|||||
p |
||||||
0 |
|
|
|
|
|
|
В результате получим:
t |
|
1 |
|
t |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
∙ |
e pt |
|
f |
|
d |
|
|
|
|
f |
|
t |
|
e pt dt |
||
f d |
|
|
|
|
p |
|
|
||||||||||
∙= |
p |
|
|
|
|
|
|
|
|
|
|||||||
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6.2.8. Интегрирование изображения |
|
|
|
||||||||||||||
Если |
f t =∙ F p , |
и |
если |
|
несобственный |
||||||||||||
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F q dq сходится, то
p
1p F p .
интеграл
f |
t t |
|
|
∙=∙ F q dq , |
(6.22) |
p
т.е. интегрированию изображения в пределах от p до ∞ соответствует деление оригинала на t.
Доказательство. Используя формулу (6.1) и изменяя порядок интегрирования, получаем:
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
F q dq |
|
|
e qt dq f t dt |
|
|
e qt |
|
f t dt |
|||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
t |
p |
|
||||
|
|
|
|
p |
|
|
0 |
p |
|
0 |
|
|
|
|
|
|
1 |
|
|
|
f |
t |
|
|
|
|
|
|
|
||
|
|
|
f t e pt dt ∙=∙ |
|
|
|
. |
|
|
|
|
|
|
||
t |
|
|
|
t |
|
|
|
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.2.9. Изображение степенных функций |
|
||||||||||
|
|
|
|
Гамма-функцией Эйлера называется функция: |
|||||||||||
|
|
a ta 1e t dt . |
(6.23) |
0 |
|
80
