Теория функций комплексного переменного и операционное исчисление. Бондарев А.В., Ряжских А.В

ВВЕДЕНИЕ

Комплексные числа, функции комплексного переменного и методы операционного исчисления в настоящее время широко применяются в инженерных расчетах, в частности, при решении задач электротехники и радиотехники. Поэтому современному инженеру необходимо знание этих разделов математики и умение применять их для решения практических задач.

В предлагаемом учебном пособии в сжатом виде изложены основы теории функций комплексного переменного и операционного исчисления.

Учебное пособие состоит из 8 глав, в которых изложены следующие разделы: комплексные числа и функции комплексного переменного, дифференцирование функций комплексного переменного, интегрирование функций комплексного переменного, ряды в комплексной плоскости, теория вычетов, преобразование Лапласа, обратное преобразование Лапласа, применения преобразования Лапласа. Наряду с теоретическим материалом, по каждой теме разобраны примеры решения задач.

Материал, представленный в учебном пособии, соответствует рабочим программам по направлению 11.03.01 "Радиотехника", профиля "Радиотехнические средства передачи, приема и обработки сигналов" и по специальности 11.05.01 "Радиоэлектронные системы и комплексы", профиля "Радиоэлектронные системы передачи информации", дисциплине "Математика".

3

1.КОМПЛЕКСНЫЕ ЧИСЛА И ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

1.1. Комплексные числа и действия с ними

Комплексным числом называется число вида

действительной и мнимой частями комплексного числа z и

обозначаются x Re z , y Im z . Два комплексных числа счи-

таются равными, если равны порознь их действительные и мнимые части.

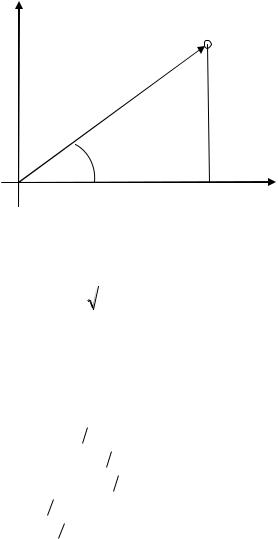
Будем изображать комплексное число z x iy с помо-

щью точки на плоскости, абсцисса которой равна x, а ордината равна y (рис. 1.1.). Тогда всякое комплексное число изобразится с помощью определенной точки на плоскости, называемой

комплексной плоскостью, и, обратно, всякой точке x, y

плоскости будет соответствовать определенное комплексное число z x iy . Комплексное число с мнимой частью, равно

нулю, т.е. x i 0 x , есть действительное число. Действительные числа изображаются точками на оси Ox; эту ось будем называть действительной осью. Комплексные числа с действительной частью, равной нулю, т.е. 0 i y i y , называются

чисто мнимыми числами. Они изображаются с помощью точек, лежащих на оси Oy, эту ось будем называть мнимой осью.

Положение точки M x, y , изображающей комплексное число z, можно определять также с помощью полярных координат r, . Числа r и будем называть соответственно модулем и аргументом комплексного числа z и пользоваться обозначениями: r z , Arg z . Из определения модуля и аргумента следует, что если z x iy , то

4

Y

y M

Величина Arg z многозначна и определена лишь с точ-

ностью до числа, кратного 2 . В качестве главного значения аргумента обычно выбирают значение, удовлетворяющее неравенству . Главное значение аргумента z обознача-

5

С помощью формулы Эйлера

можно перейти от тригонометрической формы к показатель-

ной:

Два комплексных числа, имеющих одну и ту же действительную часть, а мнимые части равные по величине, но противоположные по знаку, называются взаимно сопряженными. Если z x iy , то сопряженное ему число z x iy . Модули

взаимно сопряженных чисел одинаковы, а аргументы отличаются только знаком.

Сложение, вычитание и умножение комплексных чисел производится по правилам сложения, вычитания и умножения

произведенных над комплексными числами, следует отделить действительную часть от мнимой, т.е. собрать отдельно члены, не содержащие множителя i, и члены, содержащие этот множитель.

Произведение двух взаимно сопряженных комплексных чисел является действительным числом, равным квадрату модуля этих чисел:

6

Деление комплексных чисел определяется как действие, обратное умножению. Пользуясь свойствами сопряженных чисел, удобнее всего деление комплексных чисел производить следующим образом: сначала умножить делимое и делитель на число, сопряженное делителю, после чего делитель станет действительным числом, а затем произвести деление действительной и мнимой частей отдельно:

7

Из правила умножения (1.13) следует правило возведения в целую положительную степень:

где k – любое целое число.

Соотношение (1.17) называется формулой Муавра. Извлечь корень целой положительной степени из числа z

– значит найти такое число w, для которого выполняется равенство wn z . Если ввести обозначения z r cos i sin ,

w cos isin , то в соответствии с правилом возведения

встепень имеем:

cos i sin n r cos i sin

или

n cos n i sin n r cos i sin .

Следовательно, n r , n 2k . Так как r и – положительные числа, то из первого равенства получим nr . Из

второго равенства находим: 2k . n

Таким образом, формула для извлечения корня n-й степени из комплексного числа имеет вид:

торые можно найти, полагая k 0,1, 2,..., n 1.

На комплексной плоскости точки, соответствующие значениям nz , являются вершинами правильного n-угольника,

вписанного в окружность радиуса nr с центром в начале координат.

8

Если обозначить nzm z n , то действие возведения комплексного числа в степень окажется определенным для любого рационального показателя степени.

1.2. Последовательность комплексных чисел

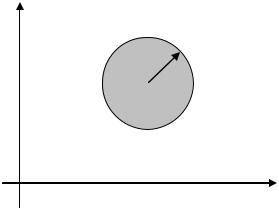
Внутренность круга радиуса с центром в точке z0 , т.е.

Число z0 называется пределом последовательности ком-

любого положительного числа можно подобрать такое число

бы ни была мала -окрестность точки z0 , все точки последова-

тельности, начинач с некоторого номера n M , попадут внутрь этой -окрестности.

9

Y

z0

O X

Рис. 1.2.

Если zn xn iyn , z0 x0 iy0 , то существование предела

lim zn z0 равносильно существованию двух пределов:

n

Пусть последовательность z1 , z2 ,..., zn ,... такова, что мо-

дули всех ее членов, начиная с некоторого, становятся больше любого, сколь угодно большого, положительного числа. Тогда говорят, что предел последовательности бесконечен, и пишут:

lim zn .

n

Для изображения этого предела дополним комплексную плоскость точкой, которую будем называть бесконечно удаленной точкой. Окрестностью бесконечно удаленной точки будем называть внешность круга достаточно большого радиуса. Комплексную плоскость, дополненную бесконечно удаленной точкой, будем называть расширенной плоскостью.

Последовательность, имеющую конечный предел, назы-

вают сходящейся.

10