
Расчёты на прочность при плоском изгибе балок. методические указания к выполнению расчётно-проектировочной работы. Попов С.П., Суднин В.М
.pdf
РАСЧЁТЫ НА ПРОЧНОСТЬ ПРИ ПЛОСКОМ ИЗГИБЕ БАЛОК
Методические указания к выполнению расчѐтно-проектировочной работы
по дисциплине «Сопротивление материалов» для студентов направлений 270100.62 «Архитектура»
и 270300.62 «Дизайн архитектурной среды»
Воронеж 2014
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждения высшего профессионального образования
«Воронежский государственный архитектурно–строительный университет»
Кафедра строительной механики
РАСЧЁТЫ НА ПРОЧНОСТЬ ПРИ ПЛОСКОМ ИЗГИБЕ БАЛОК
Методические указания к выполнению расчѐтно-проектировочной работы
по дисциплине «Сопротивление материалов» для студентов направлений 270100.62 «Архитектура
и 270300.62 «Дизайн архитектурной среды»
Воронеж 2014
УДК 624
ББК 30.121
Составители С.П. Попов, В.М. Суднин
Расчѐты на прочность при плоском изгибе балок: метод. указания к выполнению расчѐтно-проектировочной работы по дисциплине «Сопротивление материалов» для студентов направлений 270100.62 «Архитектура» и 270300.62 «Дизайн архитектурной среды»/ Воронежский ГАСУ; сост.: С.П. Попов, В.М. Суднин. – Воронеж, 2013. – 34 с.
Даны рекомендации по выполнению расчѐтно-проектировочной работы, условия и варианты задач, входящих в расчетно-проектировочную работу. Приведены краткие теоретические сведения и основные расчѐтные формулы по теме расчѐтно-проектировочной работы. Даѐтся пример выполнения работы с подробными комментариями и рекомендациями. Даны рекомендации и приведены примеры решения подобных задач на ПЭВМ с использованием популярного математического пакета Mathcad.
Предназначены для студентов дневной формы обучения. Табл. 1 .Ил. 13. Библиогр.: 4 назв.
УДК 624
ББК 30.121
Печатается по решению научно-методического совета Воронежского ГАСУ
Рецензент – А.В. Резунов, канд. физ.-мат. наук, доцент кафедры строительной механики Воронежского ГАСУ
3
ВВЕДЕНИЕ
Впроцессе изучения курса «Сопротивление материалов» студенты выполняют расчетно-проектировочные работы (РПР). Цель РПР - сознательное усвоение теоретического курса и приобретение навыков решения задач, имеющих как академический, так и практический характер. Количество РПР и задач, входящих в каждую из этих работ, определяется рабочей программой дисциплины «Сопротивление материалов» для каждого направления (специальности).
Для студентов, обучающихся по направлениям 270100.62 «Архитектура»
и270300.62 «Дизайн архитектурной среды», рабочей программой дисциплины «Сопротивление материалов» предусмотрено выполнение двух расчетнопроектировочных работ по темам: «Расчеты на прочность и жесткость при центральном растяжении – сжатии» и «Расчеты на прочность при плоском изгибе балок».
Вданных методических указаниях даны общие рекомендации по выполнению расчѐтно-проектировочной работы, условия и варианты задач, входящих в расчетно-проектировочную работу по теме «Расчеты на прочность при плоском изгибе балок». Приведены краткие теоретические сведения и основные расчѐтные формулы по теме расчѐтно-проектировочной работы. Даѐтся пример выполнения работы с подробными комментариями и рекомендациями. Даны рекомендации и приведены примеры решения подобных задач на ПЭВМ с использованием популярного математического пакета Mathcad.

4
1.РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ПЛОСКОМ ИЗГИБЕ
1.1.Основные понятия и определения
Изгиб – такой вид деформирования, при котором в поперечных сечениях бруса возникают изгибающие моменты.
Изгиб называют чистым, если в поперечных сечениях бруса возникают только изгибающие моменты. Если кроме изгибающих моментов в поперечных сечениях бруса возникают поперечные силы, то изгиб называют поперечным.
Брус, подверженный изгибу, принято называть балкой.
Изгиб называют прямым (или плоским), если все приложенные к балке нагрузки располагаются в плоскости, проходящей через ось балки и одну из главных осей инерции поперечного сечения. При прямом изгибе изогнутая ось балки - это плоская кривая, расположенная в плоскости действия нагрузок.
При прямом поперечном изгибе в вертикальной плоскости в поперечных сечениях балки возникают два внутренних силовых фактора: поперечная сила
и изгибающий момент |
. Величины |
и |
определяются методом |
сечений. |
|
|
|
Согласно методу сечений поперечная сила |
|
в сечении балки численно |
|
равна алгебраической сумме проекций на вертикальную ось сечения всех внешних сил, действующих по одну сторону от рассматриваемого сечения, т.е. на отсеченную часть балки:
|
∑ |
(1.1) |
Изгибающий момент |
в сечении балки численно равен алгебраической |
|
сумме моментов всех нагрузок, действующих на отсеченную часть балки, относительно оси , проходящей через центр тяжести данного сечения и перпендикулярной плоскости действия нагрузок:
∑ . (1.2)
Для поперечной силы и изгибающего момента вводятся следующие правила знаков.
Нагрузка, поворачивающая отсеченную часть балки относительно рассматриваемого сечения по часовой стрелке, дает положительную поперечную силу (т.е. положительное слагаемое в выражении ) и наоборот (рис. 1).
Рис. 1. Правило знаков для поперечной силы

5
Нагрузка, создающая относительно рассматриваемого сечения момент, изгибающий балку выпуклостью вниз (и создающий сжатие в верхних волокнах балки), дает положительный изгибающий момент (положительное слагаемое в выражении ) и наоборот (рис. 2).
Рис. 2. Правило знаков для изгибающего момента
Для выявления опасных сечений, где действуют наибольшие изгибающие
моменты и поперченные силы, строят графики изменения |
и |
по длине |
||
балки, т.е. эпюры. При построении эпюр |
и |
балку разбивают на участки. |
||
Участком называют часть балки, в пределах которой закон изменения внутреннего силового фактора описывается одним аналитическим выражением. При разбиении балки на участки руководствуются следующим правилом. Границами участков являются сечения, в которых приложены сосредоточенные силы, сосредоточенные моменты, а также места резкого изменения интенсивности распределенной нагрузки.
Записав аналитические выражения |
и |
по участкам балки, строят |
||||||||||||
эпюры |
и |
. При этом положительные значения |
откладывают выше |
|||||||||||
нулевой |
линии, а отрицательные – |
ниже. Ординаты |
эпюр |
изгибающих |
||||||||||
моментов |
|
принято откладывать |
со |
стороны |
растянутых |
волокон |
(т.е. |
|||||||
положительные значения |
откладывают ниже нулевой линии). |
|
|
|||||||||||
При построении эпюр |
|
и |
, |
а также для |
их проверки используют |
|||||||||
дифференциальные зависимости Д.И. Журавского между |
, |
и |
||||||||||||
интенсивностью распределенной нагрузки |
: |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
(1.3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В зависимостях (1.3) перед |
ставится знак «минус», если распределенная |
|||||||||||||
нагрузка направлена вниз.
Из дифференциальных зависимостей (1.3) вытекают следствия, которые
позволяют установить некоторые |
особенности эпюр |
и |
, |
а также |
контролировать правильность их построения: |
|
|
|
|
1. На участке, где нет распределенной нагрузки |
|
, поперечная |
||
сила постоянна |
, а изгибающий момент |
|
– |
линейная |
функция координаты . |
|
|
|
|

6
2. На участке балки, загруженном равномерно распределенной
нагрузкой |
, эпюра |
представляет собой прямую, |
наклонную к нулевой линии, эпюра |
– дугу квадратной параболы, |
|
обращенной выпуклостью по направлению распределѐнной нагрузки (правило паруса). Если на этом участке эпюра поперечной силы
пересекает нулевую линию, то в этом сечении на эпюре |
наблюдается |
локальный экстремум (максимум или минимум). |
|
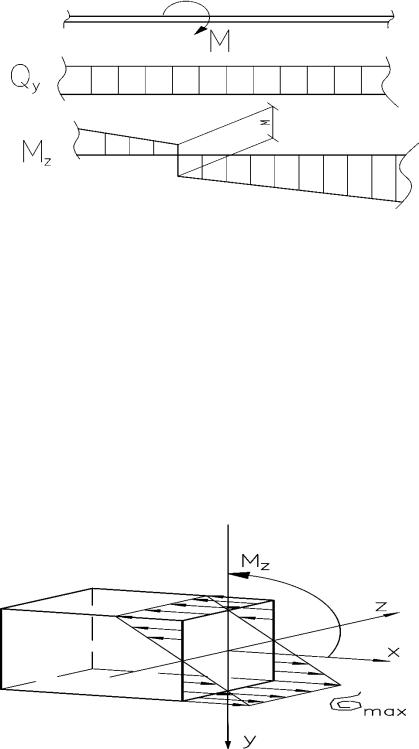
3. В сечении, где приложена сосредоточенная сила, на эпюре наблюдается скачок (т.е. скачкообразное изменение ординаты), равный по величине сосредоточенной силе, а на эпюре - излом.
7
2.В сечение, где приложен сосредоточенный момент, на эпюре наблюдается скачок, равный по величине приложенному
сосредоточенному моменту, а на эпюре |
изменений не будет. |
|
1.2. Определение напряжений и расчеты на прочность |
|||||||||
|
При плоском (прямом) поперечном изгибе в поперечных сечениях балки |
|||||||||
возникают нормальные |
и касательные |
напряжения. |
|
|
||||||
|
Нормальные напряжения вызваны изгибающим моментом и |
|||||||||
определяются по формуле |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
, |
|
|
|
(1.4) |
|
|
|
|
|
|
|
|
|
||
где |
– величина |
изгибающего |
|
момента в |
сечении |
(алгебраическая); |
||||
– |
ордината точки, |
в которой |
определяется |
; |
– |
момент |
инерции |
|||
поперечного сечения балки относительно нейтральной оси . |
|
|
||||||||
|
Из соотношения |
(1.4) видно, |
|
что |
нормальные |
напряжения |
линейно |
|||
зависят от величины . График, изображающий закон изменения нормальных напряжений по высоте сечения, называемый эпюрой напряжений, показан на рис. 3.
Рис. 3. Эпюра нормальных напряжений
8
При плоском (прямом) изгибе нейтральная ось совпадает с главной центральной осью инерции поперечного сечения, перпендикулярной плоскости действия нагрузок.
Анализ формулы (1.4) и эпюры напряжений (рис. 3) позволяет записать условие прочности при плоском изгибе по нормальным напряжениям.
При расчете на прочность по методу предельных состояний для балок из пластичных материалов это условие имеет вид
|
| | |
| |
| |
|
|
| | |
|
. |
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
или |
|
| |
|
| |
|
|
| |
| |
|
, |
(1.5) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
где |
|
|
|
|
|
|
|
|
|
. |
|
(1.6) |
|
|
|
| |
| |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
Здесь |
– осевой момент сопротивления сечения; |
|
||||||||||
| | |
– расстояние от нейтральной линии (ось z) до наиболее удаленной |
|||||||||||
точки сечения, взятое по модулю; |
|
|
|
|
|
|
||||||
– расчетное сопротивление материала по пределу текучести.
Для хрупких материалов, когда расчетные сопротивления материала балки на растяжение и на сжатие не равны (т.е. ) между собой, условие прочности записывают отдельно для растянутой и сжатой зоны поперечного сечения:
|
| |
| |
| |
| |
|
; |
|
|
|
(1.7) |
||||
|
|
|
|
|
|
|
|
|
||||||
|
| |
| |
|
|
|
|||||||||
|
| |
| |
|
|
, |
|
|
|
(1.8) |
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
где |
|
|
|
; |
|
|
|
|
|
|
|
|
. |
(1.9) |
| |
| |
|
|
|
| |
| |
|
|||||||
|
|
|
|
|
|
|
||||||||
|
В формулах (1.9) величины | | |
|
и | | |
– взятые по модулю расстояния |
||||||||||
от нейтральной линии сечения до наиболее растянутого и наиболее |
сжатого |
|||||||||||||
волокна. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Из условий прочности (1.5), (1.7) и (1.8) выполняют три вида расчетов: |
|||||||||||||
|
Проверочный расчет. Он заключается в проверке выполнения |
условий |
||||||||||||
(1.5), (1.7) и (1.8) при заданных нагрузках, материале балки, форме и размерах поперечного сечения.
Проектный расчет. Его цель – подбор поперечного сечения балки при
заданных нагрузках и материале балки. |
Из условия прочности определяют |
||||
требуемое значение осевого момента сопротивления, принимая | | |
. |
||||
Например, для балки из пластичного материала из (1.5) получим |
|
||||
|
| |
| |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По значению |
и известной форме сечения определяют его размеры или |
||||
подбирают номер стандартного прокатного профиля из таблицы сортамента. Расчет грузоподъемности. Цель этого расчета – определение
максимальных значений нагрузок, которые могут быть приложены к балке, при
9
заданных: материале балки, форме и размерах поперечного сечения, а также схеме приложения нагрузок.
Из условия прочности определяют максимальное по модулю значение изгибающего момента:
|
| | |
. |
|
По значению | | |
с использованием эпюры , которая связывает |
с |
|
приложенными нагрузками, определяют максимально допустимые значения нагрузок.
Касательные напряжения в сечении балки при плоском поперечном изгибе возникают от поперечной силы и определяются по формуле Д.И. Журавского:
|
|
| | |
, |
(1.10) |
|
|
|||
где |
– поперечная сила в сечении; |
- статический момент относительно |
||
нейтральной оси площади сечения, расположенной выше или ниже точки, в
которой определяются касательные напряжения ; в |
– ширина сечения на |
||
уровне точки, в которой определяется касательное напряжение . |
|||
Наибольшие по модулю касательные напряжения | | |
будут возникать в |
||
точках, где отношение |
| | |
достигает максимума. |
|
|
|
||
Условие прочности балки по касательным напряжениям будет иметь вид
| | |
| |
| |
| |
|
| |
. |
(1.11) |
|
|
|
|||||
|
|
|
Здесь – расчетное сопротивление материала балки на сдвиг.
Наибольшее значение | | |
берут из эпюры поперечных сил. |
Из условия прочности (1.11) могут выполняться те же три вида расчетов, что
ииз условий прочности (1.5), (1.7) и (1.8).
2.ЗАДАНИЕ НА РАСЧЕТНО-ПРОЕКТИРОВОЧНУЮ РАБОТУ ПО ТЕМЕ «РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ПЛОСКОМ ИЗГИБЕ БАЛОК»
2.1. Задача № 1. Для деревянной консольной балки, расчетная схема которой
дана на рис. 4 (схема 1), из условия прочности по методу |
предельных |
|||
состояний |
подобрать размеры |
и |
в прямоугольного поперечного сечения, |
|
приняв |
в, расчетное сопротивление дерева на растяжение |
, а |
||
расчетное сопротивление при сдвиге |
. |
|
||
Длины участков и расчетные значения нагрузок взять из табл.1. |
|
|||
2.2. Задача № 2. Для стальной балки, расчетная схема которой дана на рис. 4 (схема 2), требуется:
-подобрать из условия прочности по методу предельных состояний поперечное сечение в виде стандартного двутавра;
-для сечения, в котором действует наибольшая поперечная сила, проверить выполнение условия прочности по касательным напряжениям.
