Учебное пособие 800237

при этом сходимость суммы остающихся членов ряда HN( ) к исходной передаточной функции H( ) ухудшается и происходит отклонение частотной характеристики фильтра от первоначальной в тем большей степени, чем меньше значение N. Особенно ярко это проявляется на крутых перепадах (разрывах, скачках) в передаточных функциях:

-крутизна перепадов «размывается», т.к. она не может быть больше, чем крутизна (в нулевой точке) последней сохраненной гармоники ряда (1.11);

-по обе стороны «размытых» перепадов появляются выбросы и затухающие осцилляции с частотой, равной частоте последнего сохраненного или первого отброшенного члена ря-

да (1.10).

Эти эффекты при усечении рядов Фурье получили название явления Гиббса. Рассмотрим явление Гиббса более подробно на примере разложения в ряд Фурье частотной

функции единичного скачка G( ),которая является Фурьеобразом какой-то дискретной временной функции bn. Уравнение функции единичного скачка:

Функция (1.12) имеет разрыв величиной 1 в точке = 0 и, в силу дискретности временной функции и периодичности ее спектра, в точках , 2 и т.д. Поскольку функция G( ) является нечетной, ее ряд Фурье не содержит косинусных членов, и коэффициенты ряда определяются выражением:

9

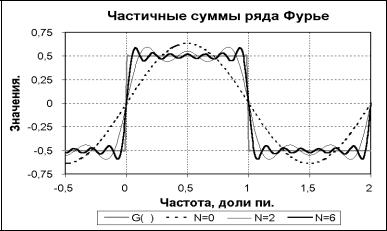
Графики частичных сумм ряда в сопоставлении с исходной функцией приведены на рис. 4. Они наглядно показывают сущность явления Гиббса.

Рис. 4. Явление Гиббса

При усечении рядов Фурье определенное искажение функции, разложенной в ряд Фурье, существует всегда. Но при малой доле энергии отсекаемой части сигнала этот эффект может быть и мало заметен. На скачках и разрывах функций он проявляется наиболее ярко.

1.3.Виды фильтров

Внастоящее время существует достаточно большое количество видов рекурсивных частотных фильтров и их различных модификаций. Наиболее известный из них - фильтр Баттерворта (рис. 5). Он имеет монотонную гладкую АЧХ во всем частотном диапазоне. При том же порядке многочленов фильтров (равном количестве полюсов) большую крутизну обеспечивают фильтры Чебышева – прямой и инверсный, однако при этом в полосе пропускания (для инверсного – в полосе подавления) у фильтров Чебышева появляются равноволновые

10

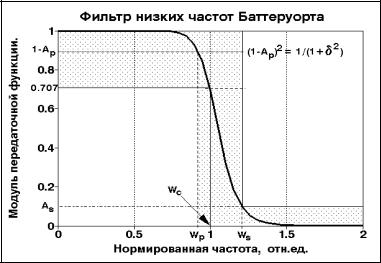
пульсации (с одинаковой амплитудой пульсаций). Еще более крутые срезы характеристик (при равноволновых пульсациях как в полосах пропускания, так и в полосе подавления) реализуются с использованием эллиптических функций.

Рис. 5. АЧХ фильтра Баттерворта

Гладкий вид амплитудно-частотной характеристики фильтра Баттерворта (см. рис. 5) задают квадратом передаточной функции вида:

|H(W)|2 = H(W)H*(W) = 1/(1+W2N),

где W = / c - нормированная частота, c -частота среза АЧХ фильтра, на которой |H( )|2 = 1/2(соответственно H( ) = 0.707), N-порядок фильтра, определяющий крутизну среза АЧХ. При W → 0 коэффициент передачи фильтра стремится к 1. Учитывая, что результаты вычислений будут относиться к цифровым фильтрам и при z-преобразовании с переходом в главный частотный диапазон произойдет искажение частот, до начала расчетов фактические значения задаваемых частотных

11

характеристик (значения c, p и s) следует перевести в значения деформированных частот по выражению:

д = (2/ t) tg( t/2) = tg( t/2), - / t< < / t.

Наклон частотной характеристики фильтра при переходе от области пропускания к области подавления можно характеризовать коэффициентом крутизны среза фильтра K в децибелах на октаву:

K = 20 log|H( 2)/H( 1)|,

где 1 и 2 – частоты с интервалом в одну октаву, т.е. 2 = 2 1. Длительность импульсной реакции фильтра в пределах ее значимой части также зависит от крутизны среза: чем боль-

ше крутизна, тем больше длительность импульсного отклика фильтра.

Функция |H(W)|2– представляет собой энергетический спектр сигнала (спектральную плотность мощности) и не имеет фазовой характеристики, т.е. является четной вещественной, образованной из двух комплексно сопряженных функций H(W) и H*(W),при этом порядок фильтра N определяет число полюсов функции H(W) и комплексно сопряженных с ними полюсов функции H*(W).

1.4. Виды аппроксимации фильтров

Характер аппроксимации фильтра зависит от выбора критерия качества аппроксимации. Кроме аппроксимации по Баттерворту существует ряд других аппроксимирующих функций: по Чебышеву, по Золотареву (Кауэру) и др.

Критерий приближения Чебышева, который широко используется не только в теории фильтров - минимум максимальной ошибки приближения (минимаксное приближение). В соответствии с этим приближением параметры передаточной

12

функции подбираются таким образом, чтобы в полосе передачи АЧХ наблюдались равноволновые пульсации коэффициента передачи, которые являются «платой» за повышение крутизны среза фильтра.

Полиномы Чебышева вычисляются по рекуррентной формуле:

Tn(W) = 2W Tn-1(W) - Tn-2(W),

T1(W) = W, To(W) = 1.

Для ФНЧ при W = / p имеет место Тn(1) = 1, |H(W)|2 = 1/(1+ 2) и значением задается коэффициент пульсаций в полосе передачи.

1.5. Аппроксимация данных

Аппроксимация данных с учетом их статистических параметров относится к задачам регрессии. Они обычно возникают при обработке экспериментальных данных, полученных в результате измерений процессов или физических явлений, статистических по своей природе (как, например, измерения в радиометрии и ядерной геофизике), или на высоком уровне помех (шумов). Задачей регрессионного анализа является подбор математических формул, наилучшим образом описывающих экспериментальные данные.

Математическая постановка задачи регрессии заключается в следующем. Зависимость величины (числового значения) определенного свойства случайного процесса или физического явления Y от другого переменного свойства или параметра Х, которое в общем случае также может относиться к

случайной величине, зарегистрирована на множестве точек xk множеством значений yk , при этом в каждой точке зарегистрированные значения yk и xk отображают действительные значения Y(хk) со случайной погрешностью k, распределенной, как

13

правило, по нормальному закону. По совокупности значений yk требуется подобрать такую функцию f(xk, a0, a1, … , an), которой зависимость Y(x) отображалась бы с минимальной погрешностью. Отсюда следует условие приближения:

yk = f(xk, a0, a1, … , an) + k.

Функцию f(xk, a0, a1, … , an) называют регрессией величины y на величину х. Регрессионный анализ предусматривает задание вида функции f(xk, a0, a1, … , an) и определение численных значений ее параметров a0, a1, … , an, обеспечивающих наименьшую погрешность приближения к множеству значений yk. Как правило, при регрессионном анализе погрешность приближения вычисляется методом наименьших квадратов. Для этого выполняется минимизация функции квадратов остаточных ошибок:

Для определения параметров a0, a1, … , an функция остаточных ошибок дифференцируется по всем параметрам, полученные уравнения частных производных приравниваются нулю и решаются в совокупности относительно всех значений параметров. Виды регрессии обычно называются по типу аппроксимирующих функций: полиномиальная, экспоненциальная, логарифмическая и т.п.

14

2. ЦЕЛИ И ЭТАПЫ КУРСОВОГО ПРОЕКТИРОВАНИЯ

Целью курсового проектирования является закрепление студентами навыков решения прикладных задач цифровой обработки сигналов. В процессе выполнения курсового проекта студенты разрабатывают ряд основных каскадов цифроаналогового преобразования сигналов.

Задание и этапы проектирования указаны в соответствующих разделах данных методических указаний. В ходе выполнения курсового проекта студенты должны приобрести необходимые практические навыки по основным методам цифровой обработки сигналов и закрепить на практике знания, полученные в лекционном курсе.

15

3. СОДЕРЖАНИЕ ПРОЕКТА

На защиту студент представляет пояснительную записку (ПЗ) в электронном и бумажном виде и полностью отлаженное программное обеспечение. Пояснительная записка должна содержать постановку задач (общую и по разделам), подробное описание выполняемых расчетов с обоснованием выбранных вариантов решения, графики в удобном для иллюстрации масштабе. Отдельные элементы графиков должны быть озаглавлены в поле рисунка и хорошо различаться в чер- но-белом варианте (Для изучения различных способов отображения линий на графике воспользуйтесь командой helpplot в командном окне).

В приложении к ПЗ должна быть приведены тексты программ с разбивкой по разделам и подробными комментариями.

16

4. ЗАДАНИЕ НА ПРОЕКТИРОВАНИЕ

Разработать тракт аналого-цифрового преобразования сигналов с преобразованием сигналов из аналоговой формы в цифровую, подавлением помех, и преобразованием цифрового сигнала с подавленными помехами из цифровой формы в аналоговую. В ПЗ приведите общую структурную схему тракта.

4.1. Формирование входного сигнала и помех

4.1.1 Сформируйте входной полигармонический сигнал вида:

( ) = ∑ × ( ),

=

где an= Kv*[1 2 1.2 2]; fn=Kv*0.01*[1 0.7 0.3 0.1]*fs; wn=2*pi*fn;

t = (0:100000-1)*ts - ось времени;

Kv = 1+0.01*(12-k) 1+0.02*(12-k) 1+0.022*(12-k) 1+0.025*(12-k)];

k– номер варианта, равный порядковому номеру в списке группы.

Набор помех вида:

( ) = ∑ × ( ),

=

ain = Kv*[5 10 10 50];

fi n=Kv*0.01*[1.1 1.28 2.5 8.2] *fs; win=2*pi*fin;

17

и белый гауссовский шумg(t) со стандартным отклонением 0.5;

fs = 1000000Гц, условная частота дискретизации входного сигнала;

ts = 1/fs;

t = (0:100000-1)*ts.

Реальный аналоговый сигнал можно рассматривать как дискретный с частотой дискретизации равной бесконечности. Входные аналоговые сигналы условно представлены дискретизированными сигналами с высокой частотой дискретизации. Соответственно, аналого-цифровой преобразователь (АЦП) моделируется как понижение частоты дискретизации входного сигнала.

4.1.2 На вход проектируемого тракта подайте входной процесс в виде суммы сигнала помех и шума:

proc(t) = s(t)+si(t)+ g(t).

4.2. Проектирование антиэлайзингового фильтра

Антиэлайзинговый фильтр (АФ) необходим для предотвращения наложения спектров после дискретизации. В качестве модели аналогового фильтра следует применить цифровой фильтр с бесконечной импульсной характеристикой (БИХ-фильтр) с аналогичными параметрами. Спроектируйте АФ порядком не выше 6-го исходя из противоречивых требований подавления внеполосных помех в дальней зоне, с одной стороны, и наименьшего искажения полезного сигнала, с другой. Источником искажений полезного сигнала является нелинейность фазо-частотной характеристики (ФЧХ) и неравномерность амплитудно-частотной характеристики (АЧХ) АФ.

18