Методические указания к практическим занятиям № 5–7 по дисциплине «Информационные технологии» для студентов специальности 090302 «Информационная безопасность телекоммуникационных систем». Разинкин К.А

ФГБОУ ВПО «Воронежский государственный технический университет»

Кафедра систем информационной безопасности

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к практическим занятиям № 5–7 по дисциплине «Информационные технологии»

для студентов специальности 090302 «Информационная безопасность

телекоммуникационных систем» очной формы обучения

Воронеж 2015

Scilab был спроектирован как открытая система, и пользователи могут добавлять в него свои типы данных и операции путём перегрузки.

В системе доступно множество инструментов: 2D и 3D

функции; интерполяция, аппроксимация; cимуляция: решение ОДУ и ДУ; Дифференциальные и не дифференциальные

программирования. В состав пакета входит утилита, позволяющая конвертировать документы Matlab в Scilab.

Scilab позволяет работать с элементарными и большим числом специальных функций (Бесселя, Неймана, интегральные функции), имеет мощные средства работы с матрицами, полиномами (в том числе и символьно), производить численные вычисления (например, численное интегрирование) и решение задач линейной алгебры, оптимизации и симуляции, мощные статистические функции, а также средство для построения и работы с графиками.

В состав пакета также входит Scicos — инструмент для редактирования блочных диаграмм и симуляции (аналог simulink в пакете MATLAB). Имеется возможность совместной работы Scilab с программой LabVIEW.

Программа доступна для различных операционных систем, включая Linux и Microsoft Windows. Возможности Scilab могут быть расширены внешними программами и модулями, написанными на разных языках программирования. Программа имеет открытый исходный код, что позволяет как свободное коммерческое использование и распространение неизменённых версий, так и некоммерческое распространение измененных версий, которые должны включать в себя исходный код.

2

Тема 5. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ В SCILAB

Если нелинейное уравнение достаточно сложное, то отыскание его корней процесс нетривиальный. Рассмотрим,

отличный от нулевого, называется алгебраическим уравнением

уравнение первой степени, квадратное - второй, кубическое - третьей и так далее.

Решение алгебраического уравнения в Scilab состоит из двух этапов. Необходимо задать полином P(x) с помощью функции poly, а затем найти его корни, применив функцию roots.

Итак, определение полиномов в Scilab осуществляет функция

poly(a, "x ["fl"]),

где a - это число или матрица чисел, x - символьная переменная, fl - необязательная символьная переменная, определяющая способ задания полинома. Символьная переменная fl может принимать только два значения «roots» или «сoeff» (соответственно «r» или «c»). Если fl=c, то будет сформирован полином с коэффициентами, хранящимися в параметре a. Если же fl=r, то значения параметра a воспринимаются функцией как корни, для которых необходимо рассчитать коэффициенты соответствующего полинома. По умолчанию fl=r.

3

Пример, отражает создание полинома p, имеющего в качестве корня тройку, и полинома f с коэффициентом 3.

Листинг 5.1. Полиномы первой степени

-->p=poly(3,’x’,’r’); -->f=poly(3,’x’,’c’);

-->p p =

- 3 + x -->f

f = 3

Далее приведены примеры создания более сложных полиномов.

Листинг 5.2. Использование функции poly

-->//Полином с корнями 1, 0 и 2

-->poly([1 0 2],’x’) ans =

2 3

2x - 3x + x

-->//Полином с коэффициентами 1, 0 и 2

-->poly([1 0 2],’x’,’c’) ans =

2

1 + 2x

Рассмотрим примеры символьных операций с полиномами:

Листинг 5.3. Примеры символьных операций с полиномами

-->p1=poly([-1 2],’x’,’c’) p1 =

- 1 + 2x

-->p2=poly([3 -7 2],’x’,’c’) p2 =

2

3 - 7x + 2x

-->p1+p2 //Сложение

4

ans = 2

2 - 5x + 2x

-->p1-p2 //Вычитание ans =

2

4 + 9x - 2x

-->p1*p2 //Умножение ans =

2 3

-3 + 13x - 16x + 4x -->p1/p2 //Деление ans =

1

-----

-3 + x

-->p1^2 //Возведение в степень ans =

2

1 - 4x + 4x

-->p2^(-1) //Возведение в отрицательную степень ans =

1

-----------

2

3 - 7x + 2x

Функция roots(p) предназначена для решения алгебраического уравнения. Здесь p это полином, созданный функцией poly и представляющий собой левую часть уравнения P(x) = 0.

Решим алгебраическое уравнение.

Для решения этой задачи необходимо задать полином p. Сделаем это при помощи функции poly, предварительно определив вектор коэффициентов V . Обратите внимание, что в уравнении отсутствует переменная x в первой степени, это означает, что соответствующий коэффициент равен нулю:

5

Листинг 5.4. Формирование полинома

-->V=[-1 0 8 -8 2]; -->p=poly(V,’x’,’c’) p =

2 3 4

1 + 8x - 8x + 2x

Теперь найдем корни полинома:

Листинг 5.5. Использование функции roots

-->X=roots(p) X =

!0.4588039 !

!- 0.3065630 !

!1.5411961 !

!2.306563 !

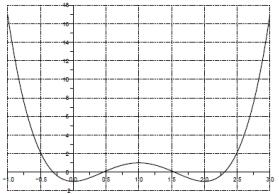
Графическое решение задачи, показанное на рис. 1, позволяет убедиться, что корни найдены верно.

Рис. 1. Графическое решение задачи 5.1.

5.1.Контрольные вопросы

1.Какая функция в SciLab отвечает за построение полиномов?

2.Каковы особенности символьных операций с полиномами. Приведите примеры.

3.Как вычисляются корни полинома. Приведите пример вычисления корней полинома четвертой степени.

6

Тема 6. ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

6.1. Метод наименьших квадратов

Метод наименьших квадратов позволяет по экспериментальным данным подобрать такую аналитическую функцию, которая проходит настолько близко к экспериментальным точкам, насколько это возможно.

Пусть в результате эксперимента были получены некоторые данные, отображенные в виде таблицы (табл. 1). Требуется построить аналитическую зависимость, наиболее точно описывающую результаты эксперимента.

Таблица 1

Экспериментальные данные

Задача сводится к определению коэффициентов ai из условия (1). Для реализации этой задачи в Scilab предусмотрена функция [a,S]=datafit(F,z,с), где F-функция, параметры которой необходимо подобрать; z-матрица исходных данных; c-вектор начальных приближений; a -вектор коэффициентов; S- сумма квадратов отклонений измеренных значений от расчетных.

Рассмотрим использование функции datafit на примере.

7

Задача 6.1. В результате опыта холостого хода определена зависимость потребляемой из сети мощности (P, Вт) от входного напряжения (U, В) для асинхронного двигателя (табл. 2).

Таблица 2 Зависимость потребляемой из сети мощности

от входного напряжения

Методом наименьших квадратов подобрать зависимость

//Функция, вычисляющая разность между экспериментальными //и теоретическими значениями.

//Перед использованием необходимо определить //z=[x;y] - матрицу исходных данных - и

//с - вектор начальных значений коэффициентов, //размерность вектора должна совпадать //с количеством искомых коэффициентов. function [zr]=G(c,z) zr=z(2)-c(1)-c(2)*z(1)-c(3)*z(1)^2-c(4)*z(1)^3 endfunction

//Исходные данные

x=[1.32 1.40 1.50 1.62 1.70 1.80 1.90...

2.00,2.11,2.20,2.32,2.40,2.51];

y=[3.30 3.50 3.85 4.25 4.50 4.85 5.40...

6.00 6.60 7.30 9.20 10.20 13.50];

//Формирование матрицы исходных данных z=[x;y];

//Вектор начальных приближений c=[0;0;0;0];

//Решение задачи

8