9.2. Расчеты на прочность и жесткость при ударе

9.2.1. Растягивающий (сжимающий) удар

9.20. Проверить прочность стального ступенчатого стержня (рис.9.17,а) при падении груза Р=4кН с высоты Н=6мм, если F=2см², =5м, Е=2·10⁵МПа, [σ]_д=160 МПа. Какое наибольшее напряжение возникает в стержне, если на кольцевой выступ А для смягчения удара поместить цилиндрическую винтовую пружину, которая при действии статической нагрузки, равной 1H, сжимается на 4·10^-4мм, т.е. жесткость пружины

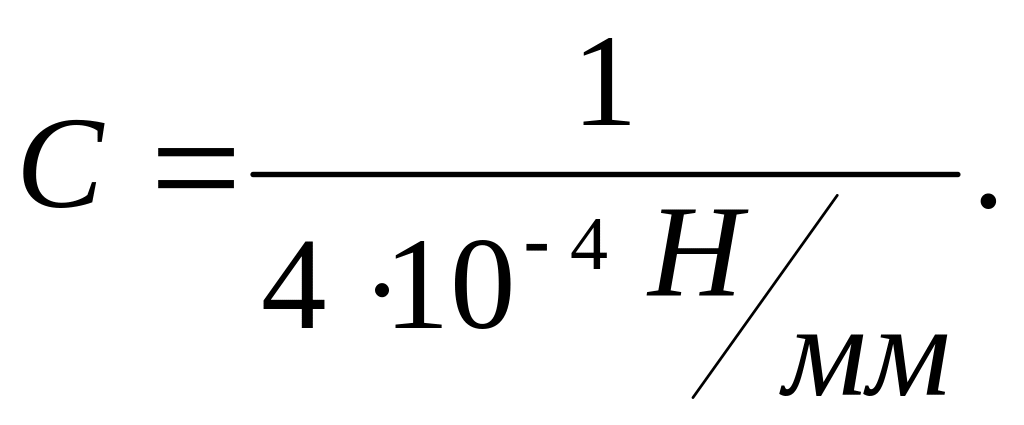
Решение

1. Записывают условие прочности

Расчет – проверочный.

2. Записывают формулу для определения коэффициента динамичности

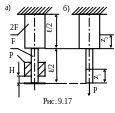
3. Вычерчивают схему статического нагружения системы силой, равной весу падающего груза, приложенной в месте удара (см. рис.9.17,б) и определяют вид деформирования – растяжение.

4. Решают статическую задачу для определения maxσ_c и δ_c=Δ _c

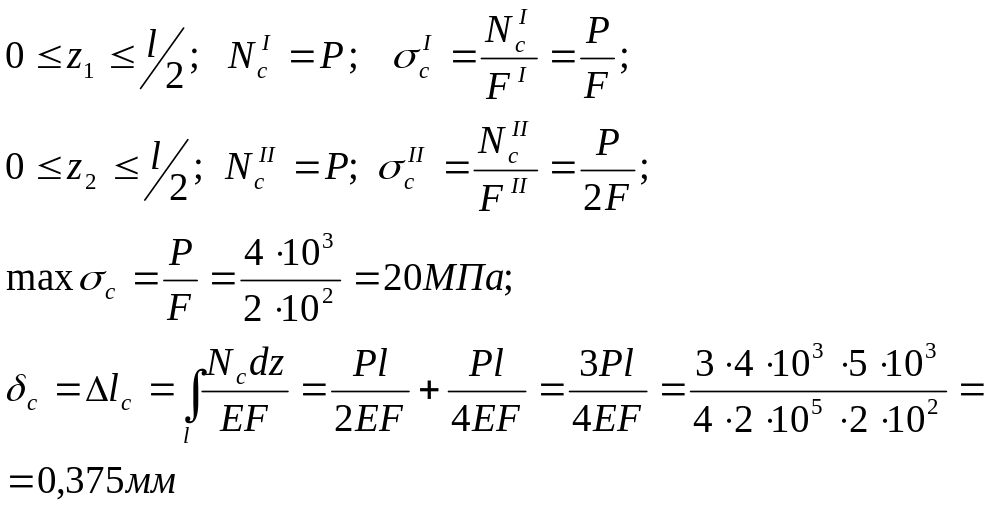
5. Определяют K_д.

Так как ,то можно определить K_д по приближенной формуле:

.

6. Проверяют выполнимость условия прочности

Условие прочности выполнено.

7. Решают задачу в предположении, что на выступе помещена пружина. В этом случае , где - осадка пружины, равная Р/С.

Так как , то K_д определяют по формуле

Определяют

Таким образом, установка пружины делает систему менее жесткой статически и более прочной при ударе, так как максимальное динамическое напряжение уменьшилось в 1,4 раза.

9.21. На диск, укрепленный на нижнем конце стального стержня (рис. 9.18,а), падает груз весом Q=80Н. Длина стержня =2м, F=4см², E=2·10⁵МПа. Считая, что [σ]_д=100МПа, определить безопасную высоту H падения груза с учетом и без учета массы стержня, если

Решение

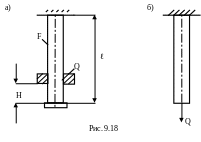
1. Записывают условие прочности

2. Записывают формулу для определения K_д в двух случаях [2]:

а) без учета массы стержня ;

б) с учетом массы стержня

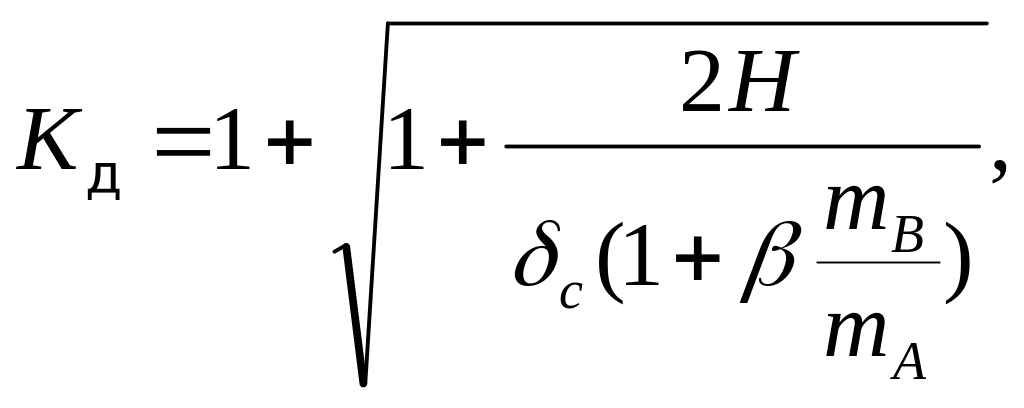
где m_А=Q/g – масса падающего груза; m_B=Flγ/g – масса стержня; β – коэффициент приведения массы стержня в точку соударения, который равен в данном случае 1/3 [2].

3. Вычерчивают схему статического нагружения стержня силой Q (см. рис. 9.18,б) и определяют вид деформирования – растяжение.

4. Решают статическую задачу

5. Определяют K_д:

а)

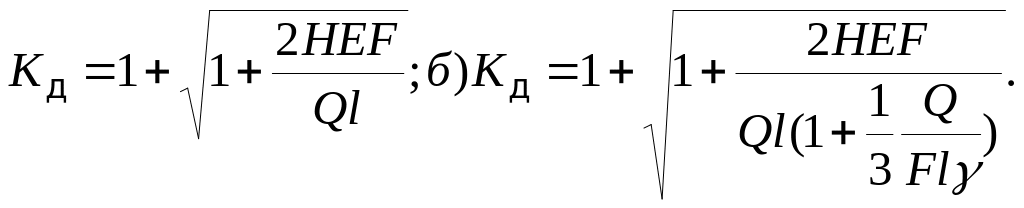
6. Подставив K_д и σ_c в условие прочности, получают уравнения для определения Н:

а)

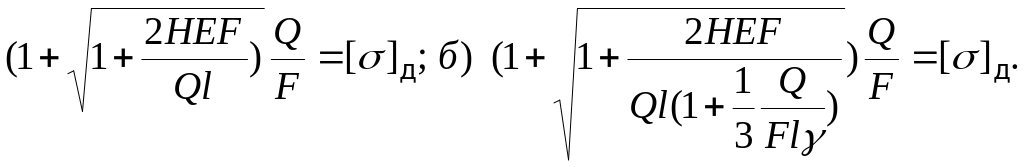
Решая (а), получают Н=249 мм; решая (б), получают Н=315мм. Следовательно, расчет не учитывающий собственный вес стержня, дает заниженное значение безопасной высоты падения груза.

9.22. Груз весом Р=15 кН, опускавшийся на стальном тросе со скоростью v=2м/с, внезапно останавливается. Проверить прочность каната, если его длина в момент остановки =100 м. Модуль упругости материала троса Е=1,7·10⁵МПа, площадь сечения F=8см², [σ]_д=200МПа. Массой троса пренебречь. Каково удлинение каната при ударе ?

9 .23. Определить напряжение, возникающее в стальном стержне переменного сечения при ударе деталью весом Р=5Н, которая движется горизонтально со скоростью v₀=5м/с (рис.9.19). Какова должна быть длина среднего участка стержня при сохранении общей длины, чтобы материал стержня не получал остаточных деформаций? Дано: а=12см, в=8 см, σ_у=320МПа, F=1см², Е=2·10⁵ МПа.

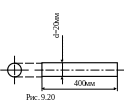
9.24. Сравнить величину наибольшего растягивающего напряжения в стальных стержнях, подвергающихся продольному удару (рис.9.20 и рис. 9.21) грузом, равным 2,5кН, обладающим в момент удара кинетической энергией Т=2Нм, если Е=2·10⁵ МПа.

9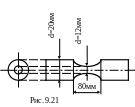 .25. Вертикальный стержень, статически растянутый силой Р, удлиняется на 1,5 мм. Определить удлинение стержня, если тот же груз растянет его, падая с высоты Н=6мм.

9.26. Сила Р=27кН мгновенно, но без удара приложена в узле А кронштейна ВАС (рис.9.22). Чему равен коэффициент запаса прочности конструкции, если F₁=4см², F₂=100см², σ_в1=400МПа, σ_в2=30МПа? Каково вертикальное перемещение узла А? Е₁=2·10⁵МПа, АВ=1м, Е₂=1·10⁴МПа.

9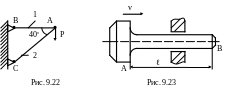 .27. Стержень АВ движется равномерно со скоростью v и останавливается вследствие удара об абсолютно жесткую опору (рис.9.23). Определить наибольшее изменение длины Δl_д стержня в момент остановки, если =0,2м, v=10м/с, E=2·10⁵МПа, плотность ρ=7,8·10⁴H/м³.

9.28. Для упругих стержневых систем, изображенных на рис. 9.24 а,б, подвергающихся удару, определить:

1) допускаемое значение падающего груза Р при Н=4 см;

2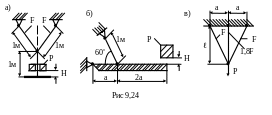 ) безопасную высоту Н падения груза при Р=100Н. Принять F=1 см², E=2·10⁵МПа, [σ]_д=160МПа.

9.29. Для заданной стержневой системы (см. рис.9.24,в) найти значение мгновенно приложенной силы Р, при которой в наиболее нагруженном стержне возникает напряжение, равное пределу пропорциональности σ_пц=250МПа. Стержни изготовлены из стали, E=2·10⁵МПа, =4м, F=5см², а=3м.

9.30. Вертикальный стальной стержень круглого поперечного сечения длиной L=5м жестко закреплен сверху и снабжен у нижнего торца кольцевым выступом. Груз Р падает вдоль стержня с высоты Н=16мм и останавливается выступом. Определить необходимый диаметр стержня, если [σ]=160МПа, E=2·10⁵МПа.