9.1.2. Кручение

9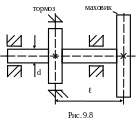 .9. Проверить прочность вала (рис. 9.8) при торможении, если вал, вращающийся со скоростью n_об=1000 об/мин, после включения тормоза останавливается, сделав n=5 оборотов. Момент инерции маховика J_m=50Нм·с². При расчете считать силу торможения постоянной и вращение вала равнозамедленным.

Принять , d=65мм.

Решение

1. Определяют вид деформирования. При торможении часть вала между маховиком и тормозом испытывает деформацию кручения.

2. Записывают условие прочности вала при торможении

3. Определяют по формуле ; Крутящий момент M_kд равен моменту от сил инерции маховика M_u , который определяется по формуле где ε – угловое ускорение при торможении.

4. Определяют ε.

При торможении ; Отсюда где - угловое перемещение вала до остановки,

5. Проверяют выполнимость условия прочности

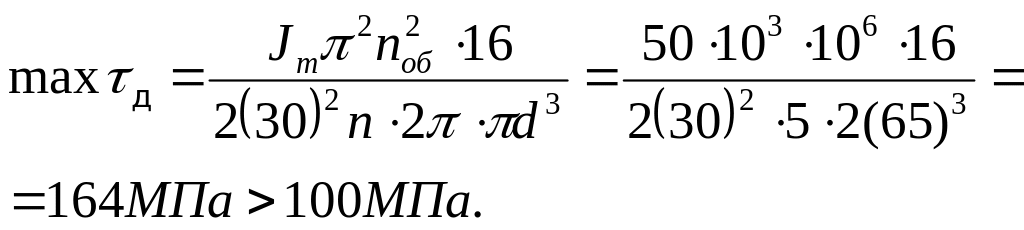
Условие прочности не выполнено.

9.10. Маховик электроинерционного стартера представляет собой диск постоянной толщины диаметром D=16 см и массой m=8 кг. За время t=10 с он разгоняется до частоты вращения n_об=8000 об/мин. Проверить прочность вала, на который насажен маховик, считая ускорение постоянным, если диаметр вала d=20мм,

9.11. На вал насажен маховик с моментом инерции J_m=0,4 кНмс². Частота вращения вала n_об=300 об/мин. После включения тормоза маховик останавливается, сделав 10 оборотов. Определить диаметр вала, если максимальное касательное напряжение в вале не должно превышать 60 МПа и сила торможения постоянна. Массой вала пренебречь.

9.1.3. Изгиб

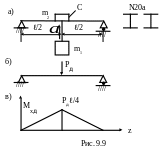
9.12. При помощи лебедки С, установленной на двух балках двутаврового сечения № 20а, поднимается груз массой m₁=5т с постоянным ускорением (рис.9.9 а). Известно, что в первые три секунды груз проходит расстояние h=10 м. Проверить прочность балок, если масса лебедки m₂=0,5т, =1м, [σ]=160 МПа.

Решение

1. Определяют вид деформирования. Вычерчивают схему нагружения балки (см. рис. 9.9б). Вид деформирования - поперечный изгиб.

2. Записывают условие прочности

3. Определяют (см. рис.9.9, в):

4. Определяют силу Р_д, которая представляет сумму веса лебедки , веса груза и силы инерции груза .

5. Определяют ускорение . Так как = const, v₀=0, то м/с².

6. Определяют и проверяют условие прочности

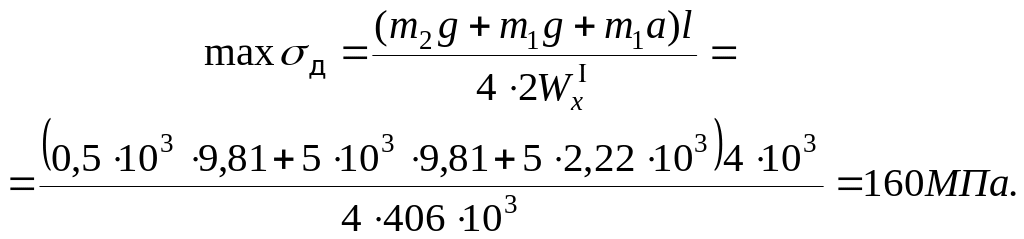
Условие прочности выполнено.

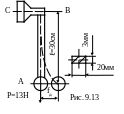
9.13. Система, изображенная на рис. 9.10, а, вращается вокруг оси ОО с постоянной угловой скоростью ω. Определить допускаемую частоту вращения n_об (об/мин), если m=1кг, R=10см. Поперечное сечение системы круглое диаметром d=1см, [σ]=160 МПа. Собственным весом системы пренебречь.

Рис. 9.10

Решение

1. Определяют вид деформирования. С учетом центробежной силы инерции расчетную схему можно представить в виде, указанном на рис. 9.10,б, где в силу симметрии изображена только левая часть. Это есть рама, нагруженная в своей плоскости. При таком нагружении расчет на прочность проводят по нормальным напряжениям.

2. Записывают условие прочности для рамы .

3. Определяют .

Для изображенной системы (см. рис. 9.10,б) опасным является сечение на оси вращения – заделка,. В этом сечении возникает продольная сила и изгибающий момент Максимальное растягивающее напряжение во внутреннем волокне заделанного сечения определяют по формуле

, .

4. Подставляют в условие прочности, из которого определяют :

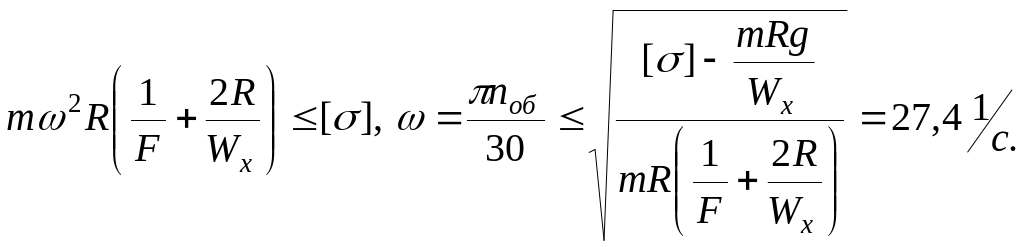
5. Определяют частоту вращения [n]_об=262 об/мин.

9.14. Швеллер №20а длиной 5 м опускается на канате со скоростью v=1,8 м/с (рис 9.14). Определить наибольшее нормальное напряжение в швеллере, если скорость опускания в течение 0,2 с равномерно уменьшилась в 3 раза, принять γ=7,8·10^-2Н/см³.

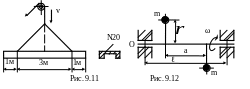9.15. К валу, вращающемуся с постоянной угловой скоростью, прикреплены два стержня, несущие на концах массы m=10 кг. Стержни расположены в одной плоскости на равных расстояниях от опор (рис. 9.12). Определить минимальное допускаемое значение диаметра вала, пренебрегая массой вала и стержней. Дано: n_об=600 об/мин, =3м, τ=0,25м, а=2м, [σ]=150 МПа.

9.16. Регулятор вращается вокруг оси B-C с постоянной скоростью n_об=90 об/мин (рис. 9.13). Считая стержень ВС абсолютно жестким, проверить прочность стального стержня АВ регулятора, а также определить горизонтальное вмещение (f_д) груза Р. Стержень АВ считать невесомым. Е=2·10⁵МПа, [σ]=160 МПа.

9.17. Стальной диск насажен на вал. В диске сделано отверстие диаметром 200мм (рис.9.14). Определить наибольшее нормальное напряжение в опасном сечении вала, вызванное наличием этого отверстия, если вал вращается с постоянной угловой скоростью ω=40 1/c. Напряжение в результате колебаний вала не учитывать. Принять γ=7,8·10^-2Н/см³.

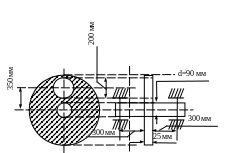
Рис. 9.14

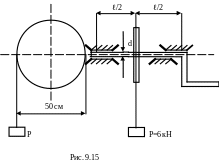
9.18. Груз Р равноускоренно поднимается на тросе, намотанном на шкив (рис.9.15). Определить площадь сечения троса и диаметр d вала по теории наибольших касательных напряжений, если [σ]_вала=100МПа, [σ]_тр=160МПа, =60см, ускорение =0,8 м/с².

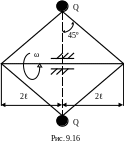
9.19. Определить угловую скорость ω вращения, при которой теряется устойчивость сжатого стержня (рис.9.16),если Е=2·10⁵МПа, =0,5м, d=2см, _пц=200МПа, Q=10 Н.