6.3. Изгиб с кручением бруса круглого поперечного сечения

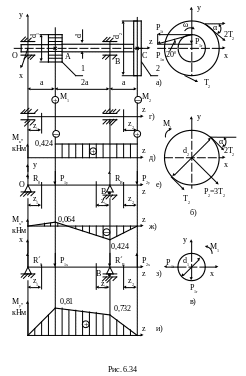
6.34. Вал зубчатой передачи (рис. 6.34) делает n оборотов в минуту. На валу жестко закреплены прямозубая цилиндрическая шестерня 1 диаметром d₁ и ведущий шкив 2 диаметром d₂ с параллельными друг другу ремнями, расположенными под углом α к горизонту, передающий вращение на вал от электродвигателя мощностью N. Усилие напряжения ремня T₂ в набегающей ветви в два раза меньше, чем в сбегающей. Используя гипотезу максимальных касательных напряжений (третью теорию прочности), определить необходимый диаметр вала, если d₁=0,2 м, d₂=0,6 м, n=630 об/мин, α=30⁰, N=28 кВт, a=0,2 м, МПа. Весом шкива и шестерни пренебречь.

Решение

1. Определяем нагрузки, действующие на вал:

а) приводим силы, действующие на шкив и шестерню к центрам тяжести соответствующих сечений вала. При приведении получаем вращающие моменты и силы, которые раскладываем на составляющие по соответствующим осям.

Шкив (см. рис. 6.34,б).

Шестерня (см. рис. 6.34,в).

Нормальную силу P_1n в зацеплении для прямозубой цилиндрической передачи раскладываем на окружную силу P_1t и радиальную P_1r = P_1t∙tg20⁰. Перенося силы, приложенные к шестерне на ось вала (см. рис. 6.34,в), получим

P_1х= P_1t , P_1y = P_1r , M₁= P_1t · d₁/2;

б) определяем вращающие моменты. Вращающий момент на шкиве [4]

Вращающий момент на шестерне определяем из условия равновесия вала (его равномерного вращения)

в) определяем составляющие усилий, действующие в сечениях А и С вала.

Сечение А

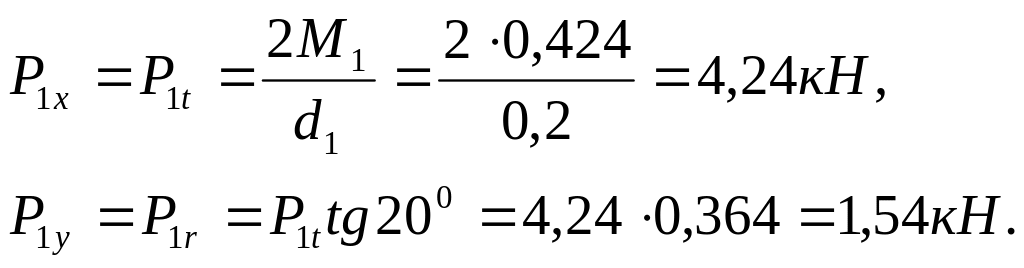
Сечение С

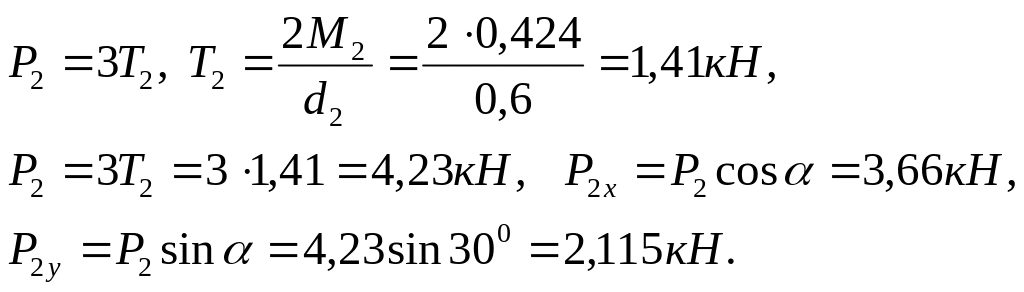
Таким образом, вал работает на кручение и изгиб в вертикальной (YOZ) и горизонтальной (XOZ) плоскостях.

2. Записываем условие прочности для круглого вала при изгибе с кручением по третьей теории прочности

где -осевой момент сопротивления вала;

- приведенный (эквивалентный) момент по третьей теории прочности. Здесь М_х, М_у – изгибающие моменты, М_k – крутящий момент.

Из условия прочности, подставив в него значение W_х, выражаем диаметр вала

Таким образом, для расчета диаметра вала необходимо определить расчетный приведенный момент, для чего вначале нужно найти величину крутящего и изгибающих моментов в опасном сечении вала.

3. Строим эпюру крутящих моментов М_k . Для ее построения составляем расчетную схему вала на кручение (см. рис. 6.34,г). Разбиваем вал на два участка, методом сечений определяем крутящие моменты на каждом из участков и по полученным значениям строим эпюру М_k (см. рис. 6.34,д).

4. Строим эпюру изгибающих моментов М_х. Для этого вначале составляем расчетную схему изгиба балки в плоскости YOZ (см. рис. 6.34,е), разбиваем балку на три участка, рассчитываем реакции опор, методом сечений определяем изгибающие моменты на каждом из участков и строим эпюру М_х (см. рис. 6.34,ж).

5. Строим эпюру изгибающих моментов М_у. Составляем расчетную схему балки в плоскости XOZ (см. рис. 6.34,з), разбиваем балку на три участка, рассчитываем реакции опор, методом сечений определяем изгибающие моменты на каждом из участков и строим эпюру М_у (см. рис. 6.34,и).

6. Рассчитываем приведенный момент. В нашем случае наиболее опасное сечение (в котором возникает максимальный приведенный момент) – это либо сечение А, либо сечение В. Какое из них опаснее непосредственно по эпюрам крутящих и изгибающих моментов установить нельзя, так как при постоянном для этих сечений моменте М_k в сечении А действуют максимальный момент М_у и небольшой момент М_х , а в сечении В – максимальный момент М_х и сравнительно большой момент М_у . В связи с этим выполним расчет для обоих предположительно опасных сечений:

Следовательно, опасным оказалось сечение В.

7. Рассчитываем необходимый диаметр вала

Принимаем, округляя до целого, d=44 мм.

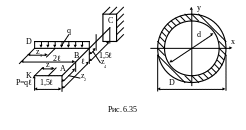
6.35. Для заданного плоскопространственного бруса кольцевого сечения (рис. 6.35) определить допускаемое значение интенсивности распределенной нагрузки q, если [σ]=160 МПа, ℓ=1 м, D=80 мм, d=0,8D. Расчет вести по энергетической (четвертой) теории прочности.

Решение

1. Оси составляющих заданную стержневую систему элементов лежат в горизонтальной плоскости, а нагрузки на нее – в вертикальной. Под действием приложенных нагрузок участки BD и АК системы работают на изгиб, а участки АВ и ВС на изгиб с кручением.

2. Записываем условие прочности для круглого вала при изгибе с кручением

где - осевой момент сопротивления полого вала; - приведенный (эквивалентный) момент по четвертой теории прочности. Здесь М_х, М_k – изгибающий и крутящий моменты соответственно.

Из условия прочности максимальный приведенный момент

Допускаемое значение интенсивности распределенной нагрузки можем определить из условия прочности, выразив предварительно через величину q.

3. Определяем изгибающие М_х и крутящие М_k моменты.

Так как стержень закреплен только в одном сечении С (жесткое защемление), то опорные реакции можно не определять. Выделяем по всей длине ломаного бруса точками ABCDK четыре участка. Границами участков являются точки приложения сосредоточенных сил, сечения, в которых происходит резкое изменение распределенной нагрузки, а также точки излома оси стержня. Свяжем с каждым поперечным сечением прямоугольную декартову систему координат x, y, z, начало которой совместим с центром тяжести сечения, ось z направим в сторону внешней нормали к сечению, а ось у – перпендикулярно плоскости расположения системы. Положение произвольного сечения на каждом из участков определим координатой z с индексом, соответствующим номеру участка (см. рис. 6.35). Записываем выражения для крутящего и изгибающего моментов на каждом участке, определяем значения М_х и М_k на границах участков и заносим их в табл. 6.1.

Таблица 6.1

Участок	Сечение
КА	К	0	0
	А	0
AB	А		0
	В
DB	D	0	0	0
	B	0
BC	B
	C

Эпюры крутящих М_k и изгибающих моментов М_х приведены на рис. 6.36.

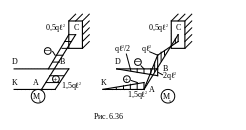
4. Устанавливаем опасное сечение и величину расчетного приведенного момента. Из таблицы 6.1 следует, что наиболее опасным является сечение В участка BD, где расчетный момент

5. Определяем допускаемое значение интенсивности распределенной нагрузки.

Подставляя значение расчетного приведенного момента в условие прочности, получим

, откуда

Принимаем [q]=2,4 кН/м.

6.36. Какой из трех видов нагружения сплошного вала диаметром D=60 мм (рис. 6.37), выполненного из пластичного материала, более опасен, если М=0,5 кНм, [σ]=160 МПа, [τ]=80 МПа?

6.37. Для заданного бруса диаметром d=30 мм (рис. 6.38) определить эквивалентные напряжения по энергетической (четвертой) теории прочности, если а=0,5 м, Р=1 кН. Как изменятся напряжения, если одну силу убрать?

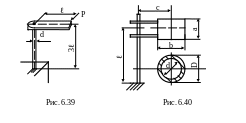
6.38. Вертикальная стойка (рис. 6.39) диаметром d=40 мм и длиной 3ℓ=90 см нагружена горизонтальной силой Р=1 кН. Проверить прочность стойки, если [σ]=160 МПа. Использовать третью теорию прочности.

6.39. Дорожный знак (рис. 6.40) закреплен на стойке трубчатого сечения с наружным диаметром D=80 мм. Стойка испытывает ветровую нагрузку интенсивностью q=1,5·10^-3 МПа. Используя теорию максимальных касательных напряжений (третью теорию прочности), определить толщину стенки, если [σ]=100 МПа. С=70 см, а=50 см, b=60 см, ℓ=200см.

6.40. Кулачок (рис. 6.41), нагруженный силой Р=3 кН, насажен на стальной вал диаметром d=50 мм. Проверить прочность вала, если [σ]=160 МПа, а=10 см, ℓ=30 см.

6.41. Для заданного стального бруса кольцевого поперечного сечения (рис. 6.42) определить допускаемое значение силы Р, если а=20 см, D=100 мм, d=0,8D, [σ]=160 МПа.

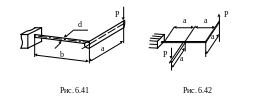
6.42. На вал круглого сечения диаметром d (рис. 6.43) от электродвигателя передается момент М=1 кНм. На валу насажен шкив диаметром D=50 см. Пренебрегая весом шкива, подобрать диаметр вала, если а=40 см, b=60 см, с=20 см, [σ]=160 МПа. Использовать третью теорию прочности.

6.43. Груз весом Р=6 кН поднимается на тросе с площадью поперечного сечения F=1 см² (рис. 6.44). Проверить прочность вала, используя теорию максимальных касательных напряжений, если D=50 см, d=60 мм, a=30 см.

6.44. Для бруса круглого поперечного сечения диаметром d=80 мм (рис. 6.45) определить допускаемое значение Р и М, если а=0,25 м, [σ]=160 МПа. Использовать теорию максимальных касательных напряжений.

6.45. На вал круглого сечения диаметром d=60 мм (рис. 6.46) передается от электродвигателя вращающий момент М. На валу насажен шкив диаметром D=50 см. Определить допускаемое значение момента М, если а=40 см, b=60 см, с=30 см. Использовать энергетическую (четвертую) теорию прочности.