10. Расчёт на прочность при переменных напряжениях

10.1. Определить величину предела выносливости при симметричном цикле изменения напряжений для изгибаемого ступенчатого вала (рис.10.1), изготовленного из стали 30 с временным сопротивлением и пределом выносливости при симметричном цикле .

Решение

Предел выносливости рассматриваемого вала можно рассчитать по формуле

. (10.1)

Здесь - масштабный коэффициент при действии нормальных напряжений; - эффективный коэффициент концентрации напряжений.

Величину коэффициента определяем по формуле

, (10.2)

где - теоретический коэффициент концентрации напряжений; q – коэффициент чувствительности материала к концентрации напряжений.

По рекомендации [2] для углеродистой стали принимаем q = 0,6. Величина для (r/d) = (5/80) = 0,0625 согласно табл. 10.1 будет равна 1,75. Тогда

.

Значение масштабного коэффициента устанавливаем по

[2] , где для d = 80мм имеем .

Таким образом, искомое значение предела выносливости рассматриваемой детали будет равно

.

Таблица 10.1

Вид деформации и фактора концентрации напряжений

1. Изгиб, растяжение (сжатие)

1.1. Полукруглая выточка на валу: отношение радиуса выточки к диаметру вала

0,1 2,0

0,5 1,6

1,0 1,2

2,0 1,1

I.2. Галтель

Отношение радиуса полной галтели к высоте сечения (диаметру вала)

0,0625 1,75

0,125 1,50

0,25 1,20

0,50 1,10

I.3. Переход под прямым углом 2,0

I.4. Отверстия при отношении диаметра последних к поперечному размеру сечения от 0,10 до 0,33 2,0

2. Кручение.

2.1. Галтель при отношении радиуса последней к диаметру вала

0,02 1,8

0,05 1,6

0,10 1,2

0,20 1,1

2 .2. Шпоночные канавки 1,6-2,0

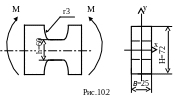
10.2. Балка прямоугольного сечения, ослабленная выточками (рис.10.2) в плоскости наибольшей жёсткости, подвергается действию изгибающего момента, меняющегося от -0,5 M_max до +M_max. Балка изготовлена из легированной стали ( = 950 МПа, = 720 МПа, = 400 МПа). Принимая основной коэффициент запаса прочности n = 1,8 определить допускаемую величину M_max.

Решение.

Величину допускаемого значения M_max при циклических нагрузках определяют из следующего условия прочности:

. (10.3)

Здесь Wx – осевой момент сопротивления; - допускаемое напряжение для материала изгибаемой детали с характеристикой цикла изменения напряжений r, определяемое по формуле

. (10.4)

Для рассматриваемой задачи в соответствии с (10.4) получим

.

Для расчёта допускаемого напряжения при симметричном цикле изменения напряжений (r = -1 ) можно использовать формулу (10.1)

Теоретический коэффициент концентрации напряжений устанавливаем согласно рис.10.3 (кривая II ) , на котором представлены изменения коэффициента при циклическом чистом изгибе [2].

2r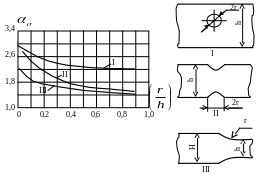

Рис.10.3

Для принимаем . Коэффициент чувствительности материала к концентраторам напряжений согласно рекомендации [2] для легированной стали с концентратором будет равен q = 0,8 .

Рассчитываем эффективный коэффициент концентрации напряжений по формуле (10.2)

.

Значение масштабного коэффициента определяем по [2] , где для d(H)=72мм. В результате получим .

Определяем величину допускаемого предела выносливости для материала изгибаемой балки при симметричном цикле нагружения

Характеристика цикла изменения напряжений r = -(0,5·M_max/M_max) = -0,5. Допускаемое напряжение при циклическом нагружении можно определить по формуле

. (10.5)

Для рассматриваемой задачи в соответствии с (10.5) получим

.

Так как осевой момент сопротивления ослабленного сечения балки равен , то искомое значение допускаемого момента согласно выражению (10.3) будет равно

.

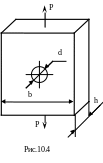
10.3. Стальная полоса с центральным отверстием (рис.10.4) подвергается циклическому растяжению-сжатию, при котором P_max=8кН, P_min=-5кН. Диаметр отверстия в полосе d=5мм, её ширина b=25мм, а толщина h=5мм. Поверхность полосы имеет шероховатость ~12,5 мкм. Материал полосы - сталь 45 с пределом прочности σ_в=500МПа и пределом выносливости . Требуется установить запас прочности детали, если [n]=1,5.

Решение

Величину коэффициента запаса усталостной прочности определяем по соотношению

(10.6)

где - соответственно амплитудное и среднее значение напряжения цикла;

- коэффициент, характеризу- ющий чувствительность материала к ассиметрии цикла ; K- коэффи- циент , учитывающий влияние основных факторов на величину предела выносливости.

Для определения напряжений предварительно рассчитываем максимальное и минимальное напряжения цикла:

;

Тогда

Величину коэффициента с

I

огласно [2] принимаем равной нулю. Коэффициент K определяем по формуле

(10.7) где - эффективный коэффициент концентрации напряжений;

- масштабный коэффициент; - коэффициент качества поверхности детали; - коэффициент упрочняющей обработки поверхности детали.

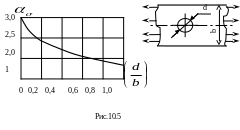
Эффективный коэффициент концентрации напряжений устанавливаем по соотношению (10.2). Коэффициент чувствительности материала к концентрации напряжений для рассматриваемой стали принимаем согласно [2] q = 0,6. Теоретический коэффициент концентрации напряжений в соответствии с рис.10.5 при будет равным . Окончательно получим

.

Для определения масштабного коэффициента можно использовать данные, представленные в [2] , где для углеродистой стали с концентратором устанавливаем, что при d(b)=25мм, коэффициент .

Величину коэффициента для принятых значений шероховатости полосы и предела прочности согласно [2] принимаем равным 0,9.

В связи с тем, что поверхность полосы не подвергается упрочняющей обработке, примем .

Подставив полученные значения коэффициентов в соотношение (10.7), получим

.

Искомый коэффициент запаса усталостной прочности согласно выражению (10.6) и полученным данным будет равен

что больше заданного в условии задачи допускаемого значения [n].

10.4. Стальной шлифованный вал с галтелью и шпоночным пазом (рис.10.6) работает на кручение по несимметричному циклу, при котором M_max =800Нм, M_min= - 200Нм. Механические характеристики материала (углеродистая сталь):

= 600МПа , =190МПа. Определить коэффициент запаса усталостной прочности при [n] = 1,5.

Решение

При оценке коэффи- циента запаса

необходимо учитывать

наличие на валу двух

концентраторов напря-

жжений: галтели и шпоночного паза.

Определим коэффициент запаса усталостной прочности с учётом галтели (d = 40мм; r = 2мм).

Номинальные характеристики цикла:

Тогда амплитудное и среднее напряжения цикла:

;

.

Определяем коэффициенты и .

Из [2] для = 600МПа следует, что = 0.

Величины коэффициентов и определяем соответственно по формуле (10.7) и (10.2), в которых следует индекс заменить на .

Для рассматриваемой стали ( ) согласно [2] принимаем q = 0,6. Теоретический коэффициент концентрации напряжений устанавливаем по табл. 10.1: для коэффициент . В итоге получим

Величину масштабного коэффициента устанавливаем также по [2], где для будем иметь . Коэффициент поверхностной чувствительности для шлифованной поверхности (шероховатость составляет 6,3мкм) и определяем по [2]: . Величину коэффициента упрочнения принимаем равным 1.

Результирующий коэффициент K на основе полученных данных

.

Подставив значение коэффициентов и характеристик цикла нагружения в соотношение (10.6), устанавливаем, что

.

Определим коэффициент запаса с учётом шпоночного паза.

В связи с тем что размеры шпоночного паза невелики по сравнению с расчётным диаметром вала (d = 40мм), принимаем приближенно значение характеристик цикла нагружения такими же, что и при определении коэффициента запаса усталостной прочности с учётом галтели.

Как и ранее принимаем .

Эффективный коэффициент концентрации устанавливаем по табл. 10.2 , где для стали с , получим .

Таблица 10.2

Эффективные коэффициенты концентрации напряжений для валов с одним и двумя шпоночными пазами

Характер нагружения	Предел прочности , МПа
	500	600	700	800	900	1000
Изгиб	1,5	1,6	1,7	1,8	1,9	2,0
Кручение	1,4	1,5	1,6	1,7	1,8	1,9

Остальные коэффициенты в соотношении (10.6) были определены ранее. Тогда искомый итоговый коэффициент

.

Окончательно с учётом всех установленных и заданных величин получаем

.

Таким образом, рассчитанные значения коэффициента n с учётом представленных концентраторов напряжений удовлетворяют условиям усталостной прочности спроектированного вала.

10.5. Определить запас прочности ступенчатого вала, изготовленного из легированной стали (рис.10.7) и работающего на циклический изгиб. Поверхность вала обточена и имеет шероховатость 12,5мкм. Цикл нагружения с имметричный M_max =0,3 кНм, M_min = -0,3 кН. Характеристики материала: , ; допускаемое значение коэффициента запаса усталостной прочности [n] = 1,5.

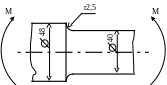
Рис.10.7

Решение

Проводим расчёт номинальных характеристик цикла:

.

В данном случае амплитудное и среднее значение напряжений цикла будут равны соответственно:

.

Так как при симметричном цикле нагружения среднее напряжение цикла равно нулю, то коэффициент можно не определять.

Эффективный коэффициент концентрации напряжений рассчитываем по формуле (10.2). При этом согласно [2] принимаем q =0,6 , а теоретический коэффициент концентрации напряжений устанавливаем по таблице 10.1 (для получим ). Тогда

.

Масштабный коэффициент определяем по [2], где находим, что для d = 40мм коэффициент .

Для заданного качества обработанной поверхности вала по [2] устанавливаем, что при и шероховатости 12,5 мкм коэффициент . В силу отсутствия упрочняющей обработки .

Результирующий коэффициент согласно соотношению (10.7) и полученным значениям коэффициентов и составит

По соотношению (10.6) и полученным данным устанавливаем, что

.

Таким образом, вал с заданными размерами обладает достаточным запасом усталостной прочности.

10.6. Ступенчатый вал (рис. 10.8) зубчатой передачи нагружен переменным напряжением изгиба симметричного цикла от момента . Вал изготовлен из углеродистой стали. Поверхность его упрочнена дробеструйной обработкой и имеет шероховатость 12мкм. Установить запас прочности вала по переменным напряжениям в сечении галтели, если [n]=2,5. Принять .

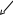
r2,5

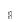
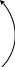
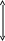
Рис.10.8

Решение

Так как вал работает на изгиб с кручением, то коэффициент запаса усталостной прочности определяем по формуле [2]

(10.8)

где - коэффициенты запаса усталостной прочности при действии соответственно только нормальных и касательных напряжений, определяемых по соотношению (10.6).

Вначале производим расчёт номинальных напряжений цикла:

;

; .

Затем определяем коэффициенты .

Как и в предыдущей задаче коэффициент не определя- ем. Для расчёта эффективного коэффициента концентрации напряжений можно воспользоваться данными таблицы (10.3): для , и принимаем . Масштабный коэффициент устанавливаем по [2], где для получим . Согласно [2] для и шероховатости 12 мкм принимаем

Таблица 10.3

Эффективный коэффициент концентрации напряжений для ступенчатых валов с диаметрами d , D и радиусом галтели r

		Коэффициент при изгибе валов с		Коэффициент при кручении валов с
			800		800
1	2	3	4	5	6
1,05	0,02 0,05 0,10 0,15 0,20	1,70 1,48 1,28 1,20 1,16	1,88 1,57 1,33 1,23 1,20	1,24 1,15 1,08 1,06 1,05	1,29 1,18 1,10 1,08 1,06
1,10	0,02 0,05 0,10 0,15 0,20	2,00 1,64 1,37 1,27 1,20	2,24 1,70 1,42 1,31 1,24	1,40 1,25 1,12 1,09 1,06	1,52 1,28 1,16 1,12 1,08
1,25	0,02 0,05 0,10 0,15 0,20	2,12 1,84 1,47 1,35 1,30	2,68 1,97 1,54 1,40 1,32	1,64 1,40 1,20 1,15 1,09	1,73 1,45 1,27 1,20 1,13

Коэффициент упрочнения определяем согласно данным [2]: для обдувки дробью детали с концентратором при d = 30- 40 мм рекомендуется назначать коэффициент в пределах 1,1-1,5 . Принимаем в решаемой задаче приближённо .

Окончательно итоговый коэффициент согласно формуле (10.8) составит

.

В соответствии с формулой (10.6) по рассчитанным и заданным значениям получим

.

При определении коэффициента запаса усталостной прочности вначале выполняем расчёт номинальных напряжений цикла

; ;

.

Значение эффективного коэффициента концентрации напряжений определяем по таблице (10.3): для , и принимаем . Значение коэффициентов будет таким же, что и при расчёте коэффициента . Тогда искомый результирующий коэффициент

.

В еличину коэффициента устанавливаем по [2], где для

Искомый коэффициент запаса усталостной прочности по касательным напряжениям

.

Общий коэффициент запаса усталостной прочности определяем по формуле (10.8):

.

Таким образом, принятые в задаче размеры вала удовлетворяют условиям усталостной прочности при заданной нагрузке.

10.7. Определить величину предела выносливости при симметричном цикле изменения напряжений для деталей, схемы нагружения и размеры которых приведены в табл. 10.4.

Детали изготовлены:

а) из углеродистой стали 20 с характеристиками: , предел выносливости при растяжении-сжатии , предел выносливости при изгибе , предел выносливости при кручении ;

б) из легированной стали 40 ХН с характеристиками , , и .

10.8. Допускаемые напряжения для детали из стали 40 ХН равны: при симметричном цикле = 120 МПа, при постоянной нагрузке = 500 МПа.

Определить величину допускаемого напряжения в следующих случаях:

1. для цикла с r = -0,5;

2. для цикла с ; ;

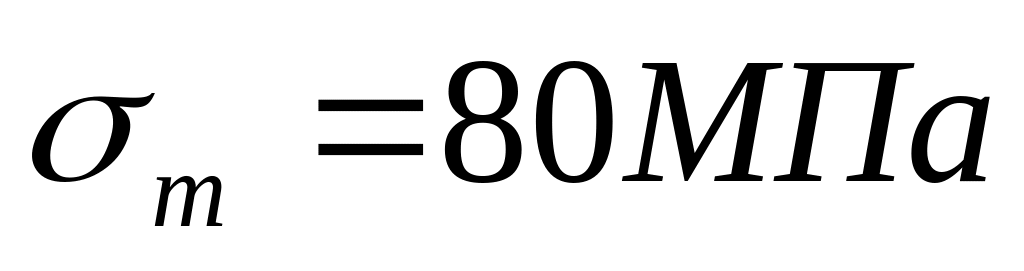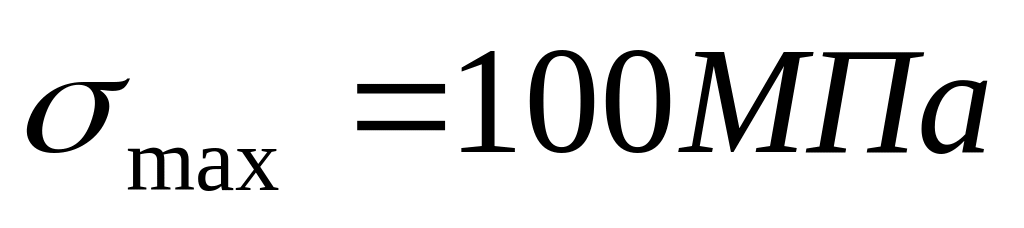3. для цикла с ; .

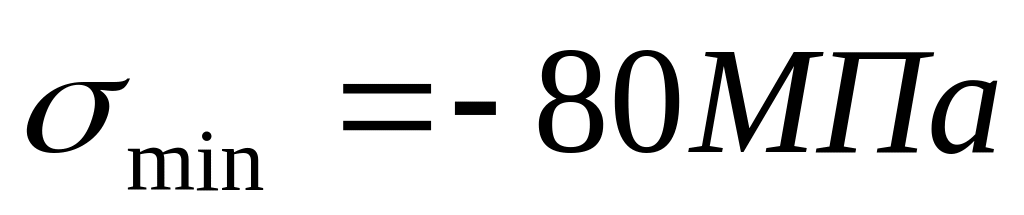Таблица 10.4

№ схем	Расчётные схемы	Размеры , мм			Вид деформи-рования
		D	d	r
1а 1б		120 60	100 50	8 5	Кручение
2а 2б		100 40	10 6		Растяжение- -сжатие
3 а 3б	Сечение прямоугольное	16 50	80 38	8 6	Изгиб

10.9. Стержень прямоугольного поперечного сечения с галтелью r =5мм (рис.10.9) из углеродистой стали 35 ( и пределом выносливости ) подвергается действию сжимающей нагрузки, изменяющейся от 0,15 до . Определить наибольшую допускаемую нагрузку , если n = 1,8 , а динамический коэффициент

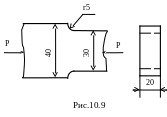
10.10. Ступенчатый вал с галтелью (рис. 10.10) из легированной стали 40Х нагружен переменным скручивающим моментом, изменяющимся по отнулевому циклу. Определить допускаемый момент, если n = 1,5 , а поверхность вала имеет шероховатость 12 мкм. Принять .

Рис.10.10

10.11. Плоский стержень (рис.10.11) из стали 45 подвергается знакопеременному растяжению-сжатию с характеристикой цикла r = -0,5 , . Поверхность стержня обработана дробью. Определить коэффициент запаса усталостной прочности .

10.12. Ступенчатый вал (рис.10.12), нагруженный моментами M = 640 Нм, вращается с постоянной угловой скоростью. Материал вала - легированная сталь ( , ). Поверхность вала шлифована.

Определить коэффициент запаса усталостной прочности.

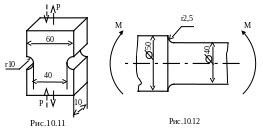
10.13. Вал, выполненный из углеродистой стали, скручивается моментами M (рис. 10.13) , меняющимися от нуля до 850 Нм. Определить коэффициент запаса усталостной прочности при , . Поверхность вала шлифована (шероховатость составляет 6 мкм).

Рис.10.13

10.14. Вращающийся вал с проточкой (рис.10.14) находится под действием моментов . Изгибающий момент постоянен, а крутящий момент меняется по отнулевому циклу. Определить коэффициент запаса усталостной прочности. Дано: ; материал – легированная сталь. Поверхность вала обдута дробью. Характеристики материала:

.

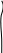
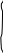
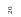
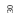
r5

Рис.10.14.

10.15. Ступенчатый вал с диаметрами d = 50мм и D = 60мм имеет в месте перехода галтель радиусом 4мм. Вал подвергается переменному изгибу с кручением . Нормальные напряжения при изгибе меняются от до , касательные напряжения при кручении изменяются от до . Материал -сталь 45 ( ).

Определить величину коэффициента запаса усталостной прочности.