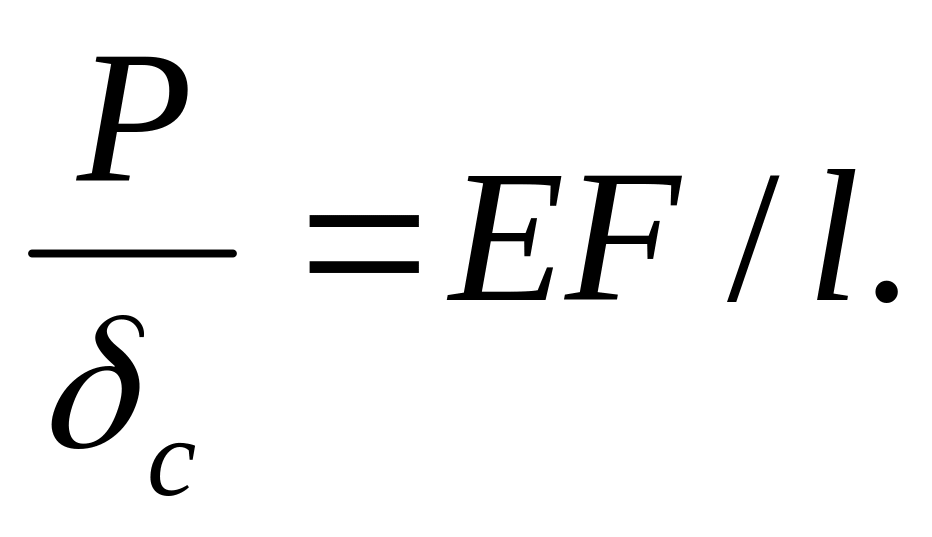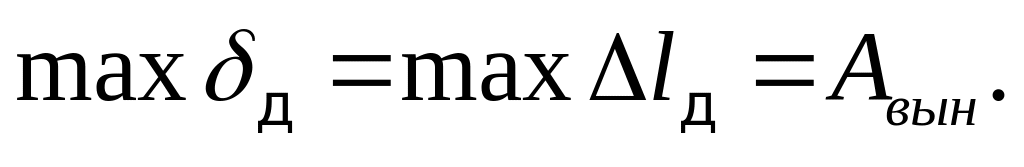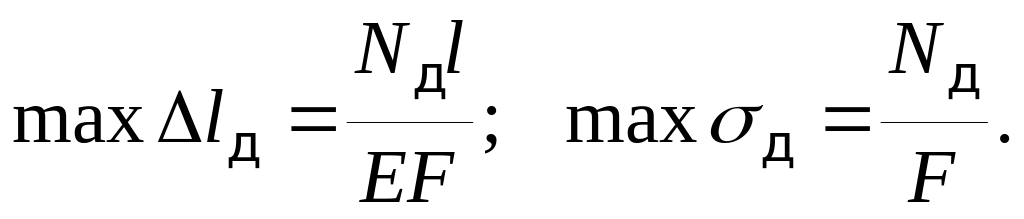9.2.2. Крутящий удар

9.31. Шкив весом Q=0,6 кН и диаметром D=240мм насажен на вал АВ (рис.9.25), вращающийся с угловой скоростью ω₀=10π рад/с. Проверить прочность вала в тот момент, когда конец вала В внезапно останавливается. Определить при этом

угол закручивания. Принять [τ]_д = 100МПа, G=8·10⁴ МПа. Массой вала пренебречь.

Решение

1. Записывают условие прочности

и формулу для определения φ_д

φ_д =K_д· φ_с..

2. Записывают формулу для определения K_д, которая при заданном условии задачи имеет вид [2]

где - кинетическая энергия шкива; - момент инерции массы шкива; U_c – потенциальная энергия вала при статическом нагружении.

3. При внезапном торможении часть вала между тормозом и шкивом скручивается.

4. Решают статическую задачу, считая М_кс=const.

;

.

5. Проверяют выполнимость условия прочности:

Условие прочности выполнено.

6. Определяют угол закручивания вала в момент его внезапной остановки

9.32. На выступ АВ, жестко закрепленный на стальном стержне, падает груз Q=200Н с высоты Н=2см (рис.9.26,а). Проверить прочность стержня, если [τ]_д=100МПа, ρ=4см, =20см, диаметр стержня d=1см, G=2,8·10⁴ МПа. Выступ АВ – абсолютно жесткий.

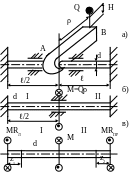
Рис. 9.26

Решение

1. Записывают условие прочности

.

2. Записывают формулу для определения динамического коэффициента, которая при заданных условиях задачи имеет вид

,

где δ_с – вертикальное перемещение точки падения груза под действием силы Q, приложенной статически в этой точке.

3. Рассматривают статическое нагружение, когда сила Q приложена на стержень к концу выступа в точке В. Вертикальное перемещение точки В зависит только от поворота выступа вокруг точки А, так как сам выступ абсолютно жесткий и сечение А не получает вертикального перемещения при указанных закреплениях. Так как выступ жестко связан с сечением стержня, то его угол поворота равен углу поворота сечения А стержня при его нагружении вращающим моментом М=Qρ (см. рис.9.26,б)

δ_c= .

4. Решают задачу статического кручения стержня

Система (см. рис.9.26,б) статически неопределимая. Раскрываем статическую неопределимость:

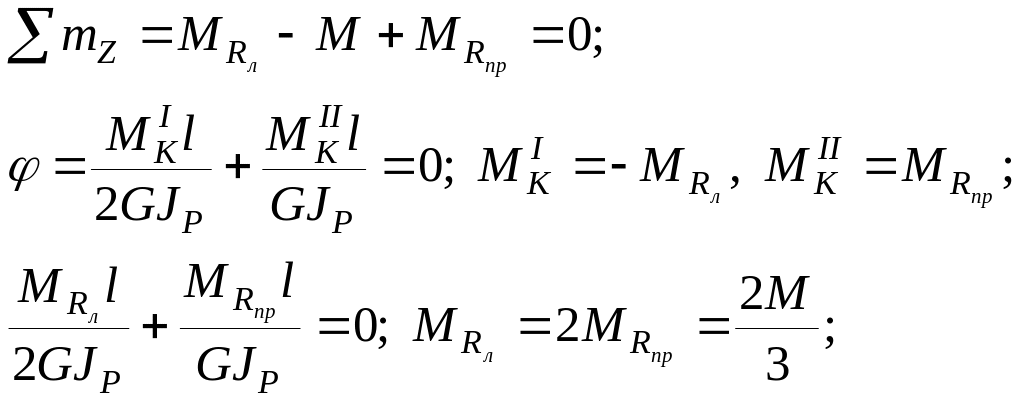
5. Проверяют выполнимость условия прочности:

Условие прочности не выполнено.

9.33. На стальной вал диаметром 100 мм насажены два маховика с одинаковыми моментами инерции J_m=300Нм·с². Расстояние между маховиками 3 м. Один маховик постоянно закреплен на валу, а другой, свободно вращающийся со скоростью 30 об/мин, посредством особого приспособления можно мгновенно сцепить с валом и привести в движение всю систему. Проверить прочность вала в момент сцепления, если [τ]_д=120МПа, G=8·10⁴МПа.

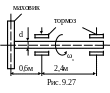
9.34. На стальной вал диаметром d=100мм, вращающийся с угловой скоростью ω₀=2π рад/c, насажен маховик, момент инерции которого J_m=180Нм·с² (рис.9.27). Определить величину наибольших динамических напряжений при внезапной остановке вала. Массу вала не учитывать. Задачу решить в двух вариантах:

а) тормозное устройство установлено на левой опоре;

б) тормозное устройство установлено на правой опоре.

9.35. Определить наибольшее допустимое число оборотов вращающегося сплошного стального диска диаметром D=80см и толщиной t=8мм, насаженного на стальной вал диаметром d=60мм так, чтобы при внезапном торможении вала в сечении, расположенном на расстоянии 1,6м от диска, наибольшее касательное напряжение в вале не превышало 100МПа. Принять γ=78·10³ Н/м³, G=8·10⁴ МПа.

9.36. Определить max τ_д в вале, вращающемся с угловой скоростью ω₀ и несущем маховик с моментом инерции массы J_m (рис 9.28) при резком зажиме вала:

а) в одном подшипнике;

б) в обоих подшипниках одновременно.

Дано: , J_m, d, G, ω₀.

9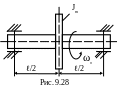 .37. Определить расстояние от маховика до тормозного устройства, если вал, вращающийся со скоростью 1000об/мин и несущий маховик с моментом инерции J_m=50Нм·с², мгновенно останавливается. Диаметр вала d=6см, G=8*10⁴МПа,

[τ]_д=100МПа.

9.2.3. Изгибающий удар

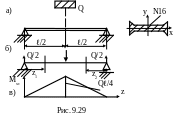
9.38. Шарнирно опертая по краям балка подвергается посередине пролета =2м удару при падении груза Q=2кН, обладающего к моменту соударения с балкой кинетической энергией Т=1,6кН·см (рис. 9.29, а). Сечение балки двутавр № 16, стойка которого расположена горизонтально. Проверить прочность балки при [σ]_д=160МПа без учета и с учетом массы балки, если γ=78кН/м³.

Решение

1. Записывают условие прочности

.

2. Записывают формулу для определения К_д, которая при заданных условиях имеет вид [2]

а) без учета массы балки ;

б) с учетом массы балки

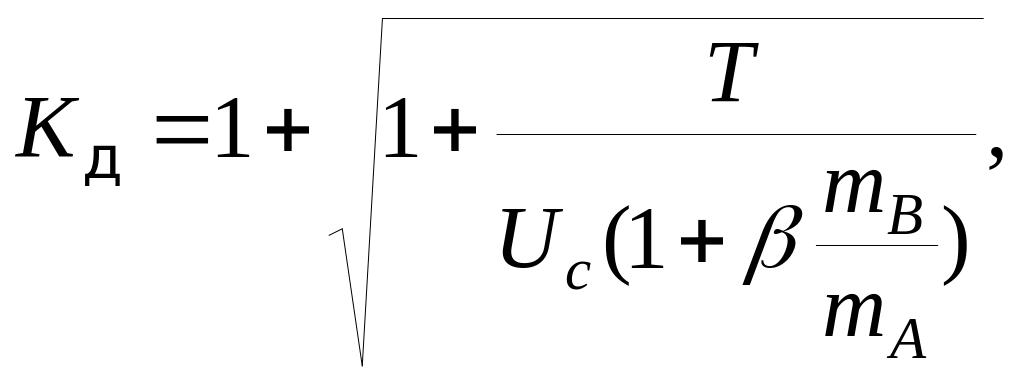
где U_C – потенциальная энергия балки при статическом приложении силы Q в точке удара; m_A=Q/g – масса падающего груза; m_B=F γ/g- масса балки; F=20,2 см² – площадь сечения двутавра №16; β – коэффициент приведения массы балки к точке удара, который в данной задаче равен 17/35 [2].

3. Вычерчивают схему статического нагружения балки силой Q (см. рис. 9.29,б.). Вид деформирования - поперечный изгиб.

4. Решают статическую задачу

Для определения maxM_хс строят эпюру изгибающих моментов M_хс (см. рис. 9.29,в)

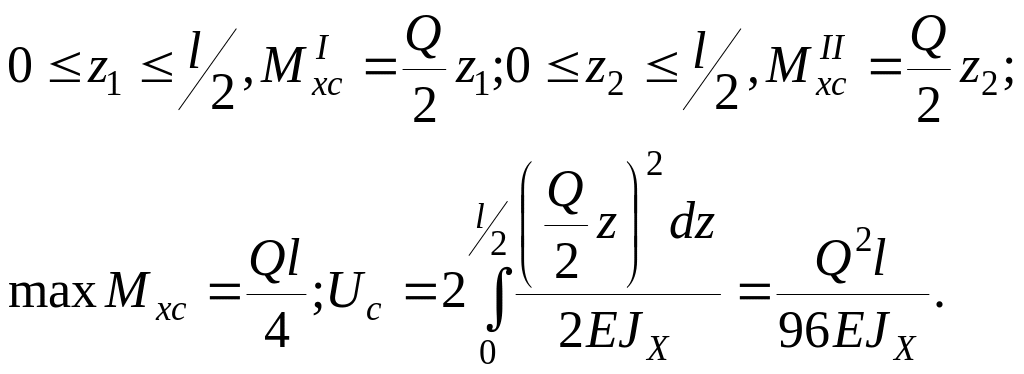
5. Определяют К_д

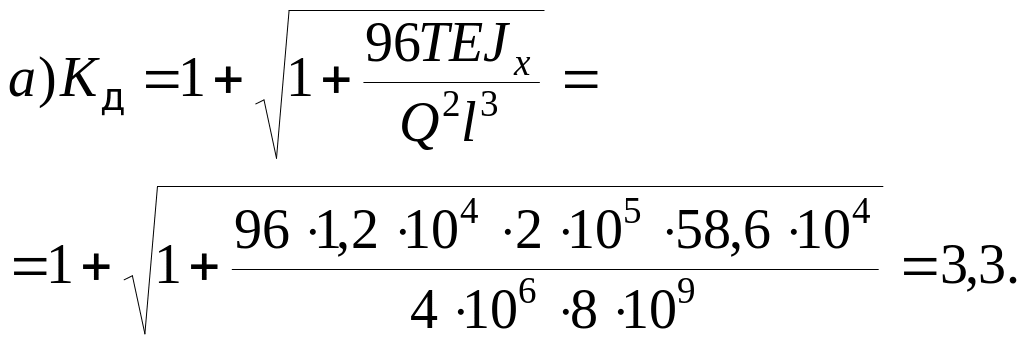
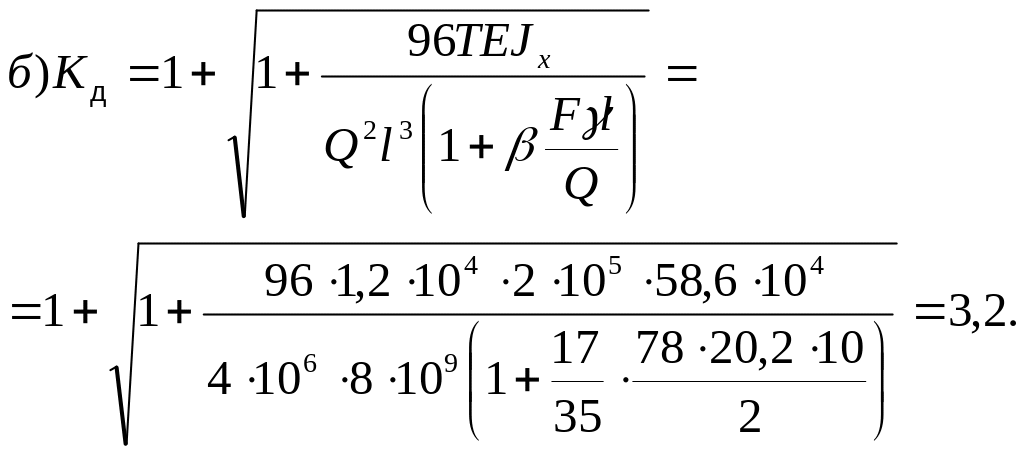В этой задаче учет собственного веса немного уменьшает динамический коэффициент.

6. Проверяют выполнимость условия прочности

а)

б)

Условие прочности не выполнено.

9.39. На стальную шарнирно опертую балку двутаврового сечения №22 а падает груз Q=1 кН посередине пролета. Какова скорость груза в момент соударения, если длина балки =2м, E=2·10⁵ МПа наибольшие нормальные напряжения при ударе σ_д=120МПа. Задачу решить без учета массы балки и с учетом ее, если γ=78кН/м³.

9.40. Решить предыдущую задачу при условии, что одна из опор упругая, т.е. ее смещение на единицу приложенной к ней нагрузки равно 4·10^-4мм/Н. Собственный вес балки не учитывать.

9.41. Груз Q=450 Н падает с высоты Н=10 см на балку, которая прогибается от удара на 2,5 см. Какая статическая нагрузка, приложенная в том же сечении балки, вызовет такой же прогиб ?

9.42. Двутавровая балка №60, шарнирно опертая по краям, подвергается посередине пролета удару грузом Q=8 кН, падающим с высоты 5 см. Стенка двутавра расположена вертикально. Определить максимальные напряжения в балке с учетом ее веса, если длина балки =4м, вес одного погонного метра равен 1,04 кН.

9.43. Деревянная балка прямоугольного поперечного сечения (h=20см,b=12 см) повергается удару грузом Q в точке В (рис.9.30). Наибольший прогиб балки в сечении D оказался равным 6мм. Чему равна высота падения груза, если Q=1кН, =1м, E=1·10⁴МПа.

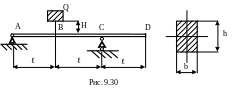
9.44. Груз весом 45 кН, приложенный посередине пролета балки, шарнирно опертой по концам, вызывает прогиб в этом сечении 2 см. Какой может быть наибольшая скорость груза весом 5 кН при его ударе по балке, чтобы прогиб балки не превышал 20 см.

9.45. На шарнирно-опертую по концам деревянную балку прямоугольного поперечного сечения 12×24 см посередине пролета =4м с высоты 5 см падает груз Q=1 кН. Определить наибольшие напряжения при изгибающем ударе по балке для двух вариантов:

а) в плоскости наибольшей жесткости;

б) в плоскости наименьшей жесткости.

9.46. К свободному концу двутавровой консольной балки длиной 1,6м внезапно без начальной скорости приложен груз Q=1,5 кН (рис.9.31). Проверить жесткость балки, если прогиб под грузом не должен превышать 2см. Модуль Юнга E=2·10⁵МПа.

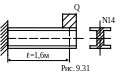
9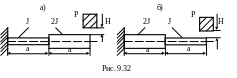 .47. На свободный край консольной балки падает груз Р. Для какой схемы нагружения (рис.9.32,а или 9.32,б) максимальный прогиб при ударе будет больше. Дано: Р, Н, Е, а, J.

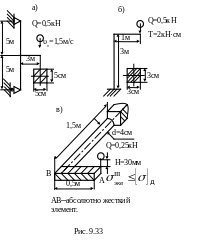
9.48. Проверить прочность при ударе систем, изображенных на рис. 9.33,а,б,в и определить прогиб в месте удара. Принять E=2·10⁵ МПа, [σ]_д=160МПа.

9.3. Вынужденные колебания упругих систем

с одной степенью свободы

9.3.1. Продольные колебания

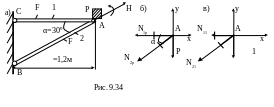
9.49. Электродвигатель весом Р=7 кН, укрепленный в узле А кронштейна ВАС (рис 9.34, а), делает n_об=2400об/мин. Центробежная сила инерции Н, возникающая вследствие неполной сбалансированности двигателя, равна 3 кН. Пренебрегая силами сопротивления и рассматривая лишь вертикальные вынужденные колебания, найти наибольшее нормальное напряжение в кронштейне и вертикальное перемещение узла А, если E=2·10⁵МПа, F=20см².

Решение

1. Так как сила Р (вес двигателя) и наибольшее значение возмущающей силы параллельны, статическое вертикальное перемещение от действия силы Р совпадает по направлению с перемещением от возмущающей силы, поэтому max σ_д и max δ_c определяет по формулам

2. Записывают формулу для определения динамического коэффициента К_д при отсутствии затухания (n=0) [2]

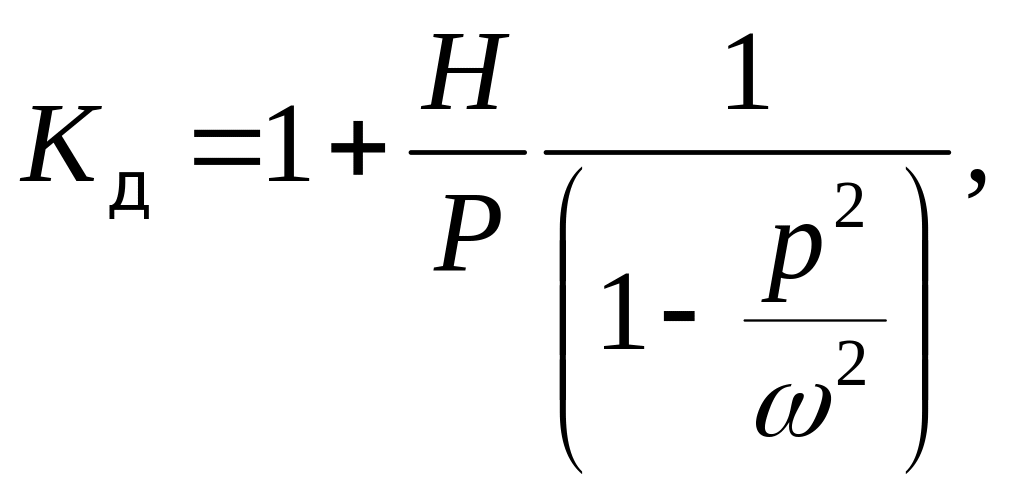
где - частота вынужденных колебаний; - частота собственных колебаний; δ_с – статическое перемещение точки приложения силы Р в направлении колебаний, то есть

3. Решают статическую задачу. Систему нагружают силой Р (рис. 9.34,б) и определяют вид деформирования – растяжение, сжатие. Для определения используют метод Максвелла-Мора (рис.9.34, в)

;

; ;

;

;

; .

- наиболее нагружен сжатый стержень.

4. Определяют ω и К_д

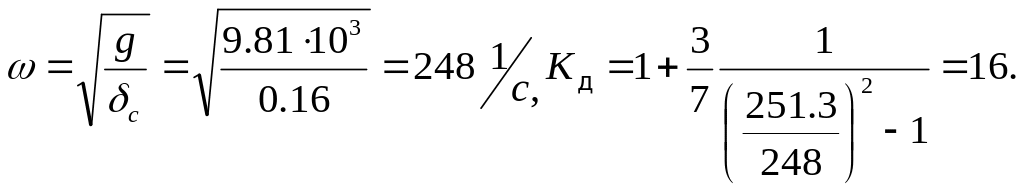
5. Определяют

9.50. Решить предыдущую задачу в предположении, что имеются силы сопротивления с коэффициентом затухания колебаний n=4с^-1. Определить длину , при которой наступит резонанс и определить при этом величину max σ_д.

9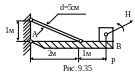 .51. На жестком брусе АВ, закрепленном, как указано на рис.9.35. установлен электромотор, вес которого Р=10кН. Центробежная сила Н, возникающая вследствие неполной уравновешенности частей двигателя, равна 4кН. Определить число оборотов мотора, при котором наступает резонaнс и наибольшие напряжения при этом, если коэффициент затухания равен n=3c^-1, E=2·10⁵МПа.

9 .52. К грузу Р=1кН, укрепленному на конце стержня длиной =1м и площадью поперечного сечения

F=1см², подвешен груз Р₁=20Н, который вращается на плече ρ=8см с частотой n_об=2400об/мин

(рис.9.36). Модуль упругости материала стержня E=2·10⁵МПа. Проверить прочность стержня, если [σ_p]=[σ]=160МПа, силы сопротивления отсутствуют, массу стержня не учитывать.

Указания:

1. Центробежная сила инерции 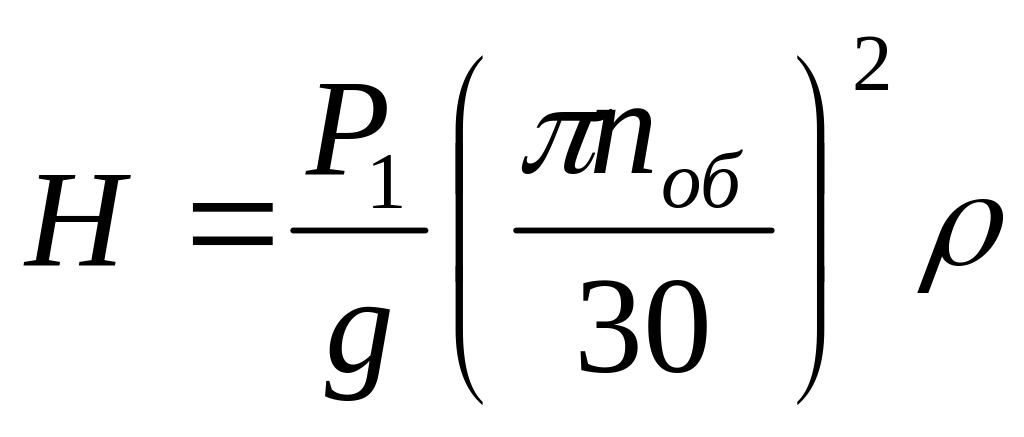вызывает продольные колебания.

2. Линейное перемещение точки приложения груза Р при статическом нагружении в направлении продольных колебаний есть удлинение 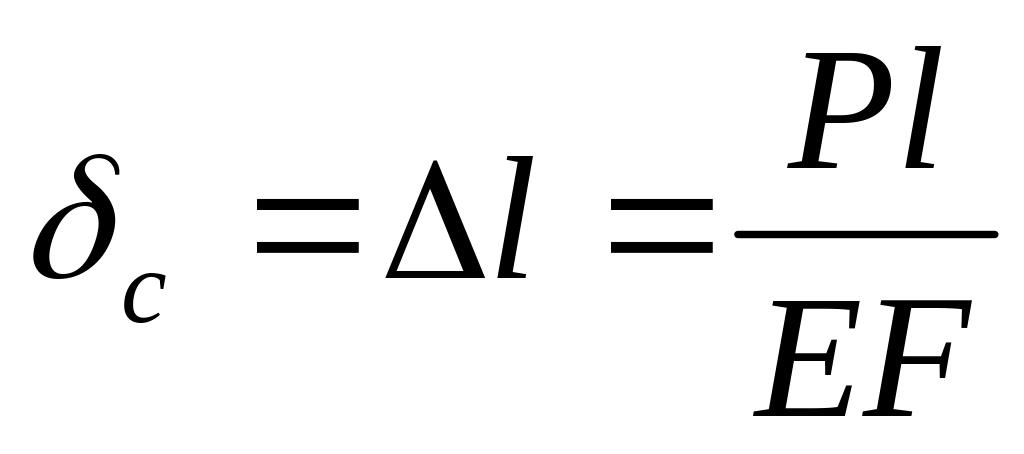. Частота собственных колебаний 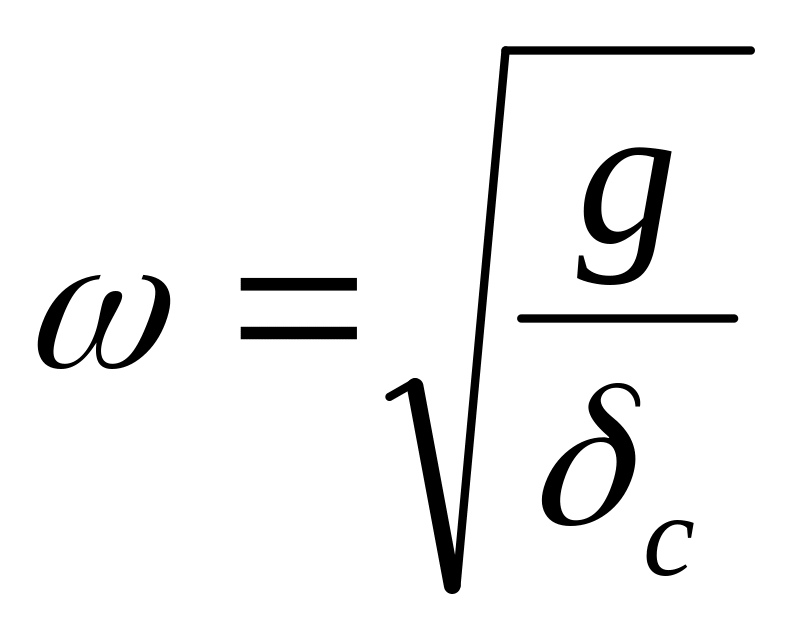, жесткость С =

3. 

4.