
- •5. Теория напряженно – деформированного состояния
- •6. Сложное сопротивление
- •6.1.2. Пространственный косой изгиб
- •6.2. Изгиб с растяжением (сжатием)
- •6.3. Изгиб с кручением бруса круглого поперечного сечения
- •7. Расчет на прочность осесимметричных
- •7 .1 Тонкостенные безмоментные оболочки
- •7.2. Толстостенные цилиндры
- •9. Задачи динамики
- •9.1.2. Кручение
- •9.2. Расчеты на прочность и жесткость при ударе
- •9.2.1. Растягивающий (сжимающий) удар
- •9.2.2. Крутящий удар
- •9.3.2. Крутильные колебания
- •10. Расчёт на прочность при переменных напряжениях
- •11. Расчет по предельному состоянию
А.А. Воропаев Ф.Х. Томилов
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ:
СБОРНИК ЗАДАЧ
ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
(СЛОЖНОЕ ДЕФОРМИРОВАНИЕ)
Учебное пособие

![]()









![]()





![]()







Воронеж 2007
ГОУВПО «Воронежский государственный
технический университет»
А. А. Воропаев Ф. Х. Томилов
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ:
СБОРНИК ЗАДАЧ
ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
(СЛОЖНОЕ ДЕФОРМИРОВАНИЕ)
Утверждено Редакционно-издательским советом
университета в качестве учебного пособия
Воронеж 2007
УДК 539.3/7
Воропаев А.А. Сопротивление материалов: сборник задач для самостоятельной работы (сложное деформирование): учеб. пособие / А.А. Воропаев, Ф.Х. Томилов; под ред. А.А. Воропаева. Воронеж: ГОУВПО «Воронежский государственный технический университет», 2007. 210с.
В учебном пособии рассматриваются методика и техника решения задач по курсу «Сопротивление материалов». Сборник охватывает специальные разделы курса, предусмотренные типовой программой для технических вузов, и содержит около двухсот задач, предназначенных для аудиторных занятий и самостоятельной работы студентов при выполнении домашних заданий в виде расчетно-проектировочных работ, а также при подготовке к контрольным работам, зачетам и экзаменам.
Учебное пособие подготовлено в электронном виде в текстовом редакторе MS Word XP и содержится в файле Сопромат7.doc.
Табл. 9. Ил. 194 . Библиогр.: 7 назв.
Рецензенты: кафедра начертательной геометрии и графики Воронежского государственного архитектурно-строительного университета (зав. кафедрой д-р техн. наук, проф. Ю.А. Цеханов);
канд. техн. наук, доц. В.А. Рябцев
© Воропаев А.А., Томилов Ф.Х.
© Оформление. ГОУВПО «Воронежский
государственный технический универ-
ситет», 2007
ВВЕДЕНИЕ
В настоящем пособии рассматриваются методика и техника решения задач по курсу «Сопротивление материалов». Сборник охватывает основные разделы курса, предусмотренные типовой программой для технических вузов и содержит около трехсот задач, предназначенных для аудиторных занятий и самостоятельной работы студентов при выполнении домашних заданий в виде расчетно-проектировочных работ, а также при подготовке к контрольным работам, зачетам и экзаменам.
Отличительной особенностью настоящего пособия является использование универсального метода сил для решения статически неопределимых задач.
Условия некоторых задач сопровождаются несколькими расчетными схемами и, таким образом, общее число задач приближается к четыремстам. Кроме того, в сборнике дан ряд задач, предназначенных для контрольных работ.
По всем темам курса в задачнике приведены задачи различной категории сложности, начиная от простейших, рассчитанных на знание основ курса и доступных практически всем студентам, и кончая задачами повышенной сложности, требующих от студентов хорошей подготовки и более глубоких знаний изучаемого курса. Задачи повышенной трудности отмечены звездочкой *. По каждой теме приведены подробные решения типовых задач с пояснениями и указаниями.
Количество задач в сборнике значительно превышает то, которое может быть использовано в процессе изучения дисциплины. Сделано это с той целью, чтобы в зависимости от особенностей рабочей программы и постановки методики преподавания каждый преподаватель мог найти достаточное количество задач по основным разделам курса. Кроме того, большое количество простых задач, включенных в сборник, позволяет рассчитывать, что он вполне может быть использован при изучении курса студентами других технических специальностей вузов.
Тематика и схемы некоторых типовых задач заимствованы из учебной литературы, список которой приведен в конце пособия. Подавляющее же большинство задач являются оригинальными и составлены специально для настоящего сборника. При этом был использован и обобщен опыт многолетнего преподавания курса сопротивления материалов в Воронежском государственном техническом университете. По каждому из разделов приводятся задачи, посвященные различным видам расчетов на прочность и жесткость.
Задачи повышенной сложности, к которым даны методические рекомендации по их решению, предназначены для студентов, проявляющих повышенный интерес к предмету, и могут быть использованы при их подготовке к олимпиадам по сопротивлению материалов.
Настоящее пособие имеет целью облегчить студентам усвоение одной из наиболее сложных инженерообразующих дисциплин, приучить их к работе над книгой и развить в них навыки самостоятельного изучения материала. Книга призвана оказать помощь студентам в овладении методами решения типовых задач, связанных с расчетами элементов конструкций на прочность и жесткость в условиях статического нагружения.
5. Теория напряженно – деформированного состояния
5.1. Определение напряжений и расчет на прочность при сложном напряженном состоянии
5.1. Участок вала диаметром d = 8 мм, проходящий через камеру высокого давления, нагружен растягивающими силами P = 6 кН и скручивается моментами m = 10 Н·м (рис. 5.1). Оценить прочность вала, если давление в камере q = 100 МПа, а материал вала –легированная сталь с [σ]p = 250 МПа и
[σ]с = 350 МПа.
Р ешение
ешение
Для обеспечения прочности вала необходимо, чтобы во всех его точках выполнялось условие прочности
![]() .
.
Поскольку [σ]p и [σ]с существенно различны, то это означает, что материал вала по-разному сопротивляется растяжению и сжатию. Поэтому для определения эквивалентного напряжения σэкв используем теорию прочности Мора, согласно которой условие прочности будет иметь вид [2]
![]() ,
,
где
![]() ;
;
![]() и
и
![]() - первое и третье главные напряжения в
наиболее нагруженной точке опасного
сечения вала.
- первое и третье главные напряжения в
наиболее нагруженной точке опасного
сечения вала.
Наличие растягивающих сил P приводит к появлению в сечения вала нормальной силы N = P постоянной по его длине. Скручивающие моменты m приводят к появлению в сечениях вала крутящего момента Mk = m, который также постоянен по длине вала.
Это позволяет сделать вывод о том, что все сечения рассматриваемого участка вала равноопасны.
Нормальная
сила N
вызывает появление в поперечных сечениях
вала нормальных напряжений
![]() ,
равномерно распределенных по площади
сечения. Давление q
приводит к появлению нормальных
напряжений в сечениях вала параллельных
оси вала Z.
Эти напряжения также постоянны и равны
-q.
Крутящий момент Mk
приводит к появлению в поперечных
сечениях вала касательных напряжений,
линейно изменяющихся по радиусу и
достигающих максимальной величины в
точках, прилежащих к наружному контуру
поперечного сечения вала. В силу закона
парности аналогичные касательные
напряжения возникают в продольных
сечениях вала.
,
равномерно распределенных по площади
сечения. Давление q
приводит к появлению нормальных
напряжений в сечениях вала параллельных
оси вала Z.
Эти напряжения также постоянны и равны
-q.
Крутящий момент Mk
приводит к появлению в поперечных
сечениях вала касательных напряжений,
линейно изменяющихся по радиусу и
достигающих максимальной величины в
точках, прилежащих к наружному контуру
поперечного сечения вала. В силу закона
парности аналогичные касательные
напряжения возникают в продольных
сечениях вала.
Проведенный анализ позволяет сделать вывод, что наиболее напряженным, а следовательно, и опасными, будут точки, прилежащие к наружному контуру сечения вала.
Плоскостями, перпендикулярными и параллельными оси вала Z, вырежем в окрестности опасной точки сечения вала элемент в виде параллелепипеда, одна из граней которого совпадает с поверхностью вала, и покажем напряжения, действующие на его видимых гранях (рис. 5.2). На гранях перпендикулярных оси Z, действуют:
![]()
 ;
;
![]() .
.
На
гранях, перпендикулярных оси Х, имеем:
![]() и
и
![]() .На
гранях, перпендикулярных оси Y,
действуют только
.На
гранях, перпендикулярных оси Y,
действуют только
![]() .
.
Определим
величины главных напряжений в
рассматриваемой точке. В этой точке
имеет место объемное напряженное
состояние. При этом одно из главных
напряжений уже известно и равно
![]() ,
т.к. на площадках, перпендикулярных оси
Y,
не действует касательные напряжения,
и, следовательно, эти площади являются
главными. Площадки действия остальных
двух главных напряжений перпендикулярны
к найденным главным площадкам и
принадлежат семейству площадок,
параллельных оси Y.
Следовательно, неизвестные главные
напряжения не зависят от
и могут быть найдены по формулам для
плоского напряженного состояния [2]:
,
т.к. на площадках, перпендикулярных оси
Y,
не действует касательные напряжения,
и, следовательно, эти площади являются
главными. Площадки действия остальных
двух главных напряжений перпендикулярны
к найденным главным площадкам и
принадлежат семейству площадок,
параллельных оси Y.
Следовательно, неизвестные главные
напряжения не зависят от
и могут быть найдены по формулам для
плоского напряженного состояния [2]:
![]() =
=
![]() .
.
Учитывая,
что по правилу обозначения главных
напряжений
![]() [2], получим:
[2], получим:
![]() ;
;
![]() ;
;
![]() .
.
П роверим
правильность определения величин
и
графическим методом. Для этого в системе
координат
роверим
правильность определения величин
и
графическим методом. Для этого в системе
координат
![]() (рис. 5.2, а) отложим отрезки ОА и ОВ,
соответствующие в выбранном масштабе
напряжениям
(рис. 5.2, а) отложим отрезки ОА и ОВ,
соответствующие в выбранном масштабе
напряжениям
![]() и
.
Из точек А и В восстановим перпендикуляры
АС и BD,
равные по величине касательным напряжениям
и
.
Из точек А и В восстановим перпендикуляры
АС и BD,
равные по величине касательным напряжениям
![]() и
и
![]() .
Соединим точки С и D
прямой линией и обозначим Е точку
пересечения прямой CD
с осью
.
Соединим точки С и D
прямой линией и обозначим Е точку
пересечения прямой CD
с осью
![]() .
С центром в точке Е строим круг Мора
радиусом, равным СЕ (или ED).
Отрезки ОK и OL,
отсекаемые кругом Мора на оси
,
дают в масштабе величины
и
.
Измеряя длины этих отрезков и умножая
из на масштаб по оси
,
получим
.
С центром в точке Е строим круг Мора
радиусом, равным СЕ (или ED).
Отрезки ОK и OL,
отсекаемые кругом Мора на оси
,
дают в масштабе величины
и
.
Измеряя длины этих отрезков и умножая
из на масштаб по оси
,
получим
![]() ,
,
![]() ,
что практически совпадает с результатом,
полученным аналитически.
,
что практически совпадает с результатом,
полученным аналитически.
Подставляя в условие прочности , , получим:
![]() ,
,
т.е. эквивалентное напряжение превышает допускаемое.
Оценим перегрузку
![]() ,
,
что вполне допустимо.
Таким образом, прочность вала обеспечена.
5.2.
Проверить прочность вала диаметром d
= 100 мм, жестко защемленного в нижнем
сечении и нагруженного, как показано
на рис. 5.3, если P
= 200 кН, M
= 6 кН·м. Материал вала – чугун с
![]() ,
,
![]() .
.
5.3. Стальной болт (рис. 5.4) с площадью поперечного сечения F = 10,0 см2, поставленный без зазора, затянут усилием P = 60 кН и стягивает две пластины, нагруженные силами T = 30 кН.
Проверить
прочность болта, считая
![]() .
.
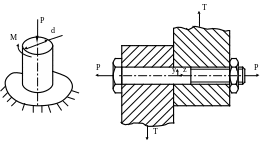
Рис. 5.3 Рис. 5.4
5.4.
В окрестности опасной точки конструкции
выделен элемент в форме прямоугольного
параллелепипеда, по граням которого
действуют нормальные и касательные
напряжения (рис. 5.5). Проверить прочность
конструкции, если ее материал – сталь
с пределом текучести
![]() ,
а требуемый коэффициент запаса прочности
,
а требуемый коэффициент запаса прочности
![]() .
.
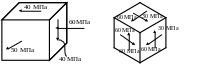
Рис. 5.5 Рис. 5.6
5.5.
В окрестности опасной точки конструкции
выделен элемент, по всем граням которого
действуют только касательные напряжения
(рис. 5.6). Определить коэффициент запаса
по текучести, если материал конструкции
– дуралюмин с
![]() .
.
5.6.
На гранях элемента, вырезанного в
окрестности опасной течки детали,
действуют нормальные
,
и касательные
![]() и
и
![]() напряжения (рис. 5.7). Оценить прочность
детали и рассчитать запас прочности,
если материал детали – сталь,
напряжения (рис. 5.7). Оценить прочность
детали и рассчитать запас прочности,
если материал детали – сталь,
![]() .
Значение напряжений приведены в табл.
5.1. Задачу решить аналитически и графически
с помощью круга Мора.
.
Значение напряжений приведены в табл.
5.1. Задачу решить аналитически и графически
с помощью круга Мора.
Таблица 5.1
Вариант |
, МПа |
, МПа |
, МПа |
1 2 3 4 5 6 7 8 9 10 |
40 50 -20 -40 -10 -20 50 0 -40 0 |
20 30 30 20 -20 -40 0 60 0 -80 |
10 20 20 30 10 40 20 30 20 20 |
5.7.
Определить коэффициент запаса по
текучести для образца АВ, помещенного
в камеру высокого давления и нагруженного
моментом М (рис. 5.8). Момент сил трения
на торце захвата А и в уплотнении С равен
0,3М. Материал образца – легированная
сталь с
![]() ,
,
![]() ,
d
= 20 мм, М = 500 Н·м. Давление в камере
,
d
= 20 мм, М = 500 Н·м. Давление в камере
q = 100 МПа.
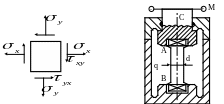
Рис. 5.7 Рис. 5.8
5.8. Определить коэффициент запаса по текучести для напряженных состояний, изображенных на рис. 5.9,а и 5.9,б (напряжения даны в МПа). При расчете использовать следующие данные из табл. 5.2.
Таблица 5.2
Предел текучести |
Значения
|
||||
а |
б |
в |
г |
д |
|
|
400 500 |
300 300 |
400 500 |
500 600 |
2500 3000 |
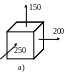
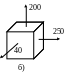

Рис. 5.9,а
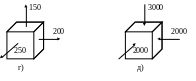
Рис. 5.9,б
5.9.
Напряженное состояние опасной точки
детали показано на рис. 5.10 (напряжения
даны в МПа). Определить коэффициент
запаса по разрушению
![]() ,
используя следующие данные из табл.
5.3.
,
используя следующие данные из табл.
5.3.

Рис. 5.10
Таблица 5.3
Предел прочности |
Значения
|
||||
а |
б |
в |
г |
д |
|
|
390 650 |
400 550 |
500 800 |
500 700 |
2200 2750 |
5.10. Короткий бетонный стержень квадратного сечения сжимается силой 400 кН. Определить размер стороны сечения стержня из условия, чтобы касательные напряжения в любом его сечении не превышали 5 МПа.
5.11. При испытании на сжатие бетонного кубика размером 20×20×20 см перед его разрушением нормальное напряжение по сечению, наклоненному под углом 45° к направлению усилия, оказалось равным –4,5 МПа. При каждой нагрузке разрушился кубик?
5.2. Обобщенный закон Гука. Определение деформаций и напряжений.
5 .12.Абсолютно
жёсткая обойма, состоящая из двух
половинок, стянута шестью болтами по
три с каждой стороны (рис. 5.11). В обойме
сжимают пластмассовую призму. Коэффициент
Пуассона пластмассы μ = 0,4. Сила, сжимающая
призму вдоль оси обоймы, Р = 100 кН.
Определить требуемый диаметр болтов,
пренебрегая деформацией обоймы и самих
болтов. Допускаемое напряжение на
растяжение для болтов
.12.Абсолютно
жёсткая обойма, состоящая из двух
половинок, стянута шестью болтами по
три с каждой стороны (рис. 5.11). В обойме
сжимают пластмассовую призму. Коэффициент
Пуассона пластмассы μ = 0,4. Сила, сжимающая
призму вдоль оси обоймы, Р = 100 кН.
Определить требуемый диаметр болтов,
пренебрегая деформацией обоймы и самих
болтов. Допускаемое напряжение на
растяжение для болтов
![]() ,
,
а = 500 мм, L = 800 мм.
Решение
При сжатии призмы длина ее уменьшается , а размеры поперечного сечения должны увеличиваться, но этому увеличению препятствуют стенки жесткой обоймы. В результате возникают силы взаимодействия между поверхностями призмы и стенками обоймы. Эти силы стремятся раздвинуть половинки обоймы и вызывают растяжение болтов. Таким образом, болты работают на растяжение и требуется провести проектный расчет, который ведется по формуле [1]:
![]() ,
,
где
F
– требуемая площадь поперечного сечения
болта;
![]() - нормальная сила, действующая в сечении
одного болта.
- нормальная сила, действующая в сечении
одного болта.
Для определения необходимо установить силы взаимодействия между сжимаемой призмой и стенками обоймы.
Сжимаемая призма находится в однородном напряженном состоянии. Напряжения в поперечных сечениях, перпендикулярных оси Z, равны:
![]() .
.
Заметим,
что в силу симметрии
![]() .
Для их определения воспользуемся
обобщенным законом Гука [2]. Учитывая,
что по условию задачи обойма абсолютно
жесткая и деформации болтов не принимаются
во внимание, заключаем, что деформации
призмы в направлениях осей X
и Y
равны нулю и, применяя обобщенный закон
Гука, с учетом того, что
,
получим
.
Для их определения воспользуемся
обобщенным законом Гука [2]. Учитывая,
что по условию задачи обойма абсолютно
жесткая и деформации болтов не принимаются
во внимание, заключаем, что деформации
призмы в направлениях осей X
и Y
равны нулю и, применяя обобщенный закон
Гука, с учетом того, что
,
получим
![]() .
.
Отсюда следует, что
![]() .
.
Давление на верхней и нижней гранях призмы равно найденному напряжению . С учетом этого, получим, что полное усилие, действующее на все болты, равно
![]() .
.
Усилие, действующее на один болт,
![]() .
.
Поскольку
![]() ,
то требуемая по условию прочности
площадь поперечного сечения болта (по
внутреннему диаметру резьбы)
,
то требуемая по условию прочности
площадь поперечного сечения болта (по
внутреннему диаметру резьбы)
![]() .
.
Отсюда находим, что минимальный диаметр болта
![]() .
.
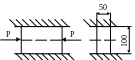 5.13.
Прямоугольный стальной брусок сечением
100×50 мм без зазора вставлен между двумя
параллельными неподвижными стенками
и нагружен в вертикальном направлении
сжимающими силами Р, равномерно
распределенными по торцам (рис. 5.12).
Вычислить допускаемую величину силы P
, если материал бруска – малоуглеродистая
сталь с
5.13.
Прямоугольный стальной брусок сечением
100×50 мм без зазора вставлен между двумя
параллельными неподвижными стенками
и нагружен в вертикальном направлении
сжимающими силами Р, равномерно
распределенными по торцам (рис. 5.12).
Вычислить допускаемую величину силы P
, если материал бруска – малоуглеродистая
сталь с
![]() ,
,
![]() ,
,
![]() .
.
Рис.5.12
5.14. Два стержня плотно, но без трения вставлены между двумя неподвижными упорами и нагружены на части длины давлением q =10 МПа (рис.5.13). Определить реакции, действующие со стороны упоров на стержни, если стержень I стальной, а стержень 2 медный. Сечение первого стержня 10х10 см, а второго 20х20 см, Ест = 2·105МПа, μст = 0,3, Ем = 1·105 МПа, μм = 0,32.
q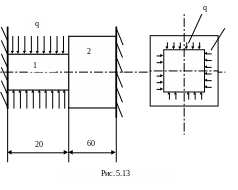
5.15. Медный стержень длиной 100 см квадратного сечения со стороной 20 см испытывает растяжение от продольной силы Р и гидростатическое двустороннее сжатие давлением q. Определить величины P и q, если в результате деформации длина стержня увеличилась на 1 мм, а длины сторон уменьшились на 0,1 мм, Ем = 1·105 МПа, μм = 0,32.
5.16.
Определить напряжения в алюминиевом
листе, закрепленном по контуру (рис.
5.14), от равномерного понижения температуры
на 50 0С.
Е = 7·104
МПа,
![]() ,
μ = 0,3. Указание. Принять, что закрепление
на контуре не препятствует равномерному
изменению толщины листа h.
,
μ = 0,3. Указание. Принять, что закрепление
на контуре не препятствует равномерному
изменению толщины листа h.
5 .17.
Алюминиевый кубик со стороной а = 50 мм
свободно, но без зазоров, вставлен в
прорезь массивной (недеформируемой)
детали (рис. 5.15) и сжат силой Р, равномерно
распределенной по верхней грани кубика.
Определить допускаемую величину силы
Р, если Еа
= 7·104
МПа, μа
= 0,3,
.17.
Алюминиевый кубик со стороной а = 50 мм
свободно, но без зазоров, вставлен в
прорезь массивной (недеформируемой)
детали (рис. 5.15) и сжат силой Р, равномерно
распределенной по верхней грани кубика.
Определить допускаемую величину силы
Р, если Еа
= 7·104
МПа, μа
= 0,3,![]() .
.

Рис.5.15
5.18.
Кубик с ребром а = 20 мм вставлен в гнездо,
сделанное в массивной плите, которую
можно считать недеформируемой (рис.
5.16). К верхней грани кубика приложена
сжимающая сила Р = 50 кН, равномерно
распределенная по площади грани. До
приложения силы Р ребра гнезда в плане
больше ребер кубика на 2δ1
= 4·10-3
мм и 2δ2
= 3·10-3
мм. Оценить прочность кубика. Материал
кубика – сталь с Е = 2·105
МПа, μ = 0,3,
![]() .
.
а
Рис. 5.16
P
![]()
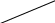














5.19. Стальной брус квадратного поперечного сечения, жестко защемленный обоими концами (рис. 5.17), на участке длиной b = 60 мм подвергается действию равномерно распределенного давления q = 150 МПа. Определить перемещение сечения I – I. Принять Е = 2·105 МПа, μ = 0,3.
1
1
q
а
Рис. 5.17
q
q












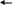
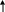
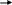
5.20. При каком соотношении между главными напряжениями возникает одноосное деформированное состояние?
5.21.
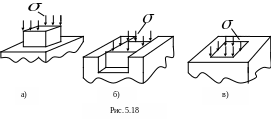
Элемент в форме куба равномерно сжимается
напряжениями
.
В каком случае изменение объема куба
будет больше: а) элемент расположен на
гладкой плите (рис. 5.18, а); б) паз (рис.
5.18, б); элемент плотно, но без натяга
вставлен в квадратное гнездо (рис. 5.18,
в)? Материал плиты во всех случаях считать
абсолютно жёстким. Принять
![]() для материала кубика.
для материала кубика.
5.22.
Для заданного поля перемещений: u=3xy2,
v=2xz,
w=z3-xy
определить тензор деформаций и объемную
деформацию
![]() .
.
5.23. В специальное приспособление помещается пластина ABCD и силой Р создается в ней деформация сдвига. Под нагрузкой тензорезисторами замеряется относительная деформация в направлении диагонали BD (l-l).Определить перемещение точки приложения силы (рис.5.19).
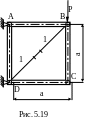
Рекомендации
Ответ
на поставленный вопрос получают на
основе кинематического анализа. При
этом, рассматривая кинематический
треугольник BCD
(см.рис. 5.19), получают соотношение
dS=δ·cos450,
где dS
– укорочение диагонали BD,
равной, например,
![]() ;
δ
– перемещение точки приложения силы
Р. На основе понятия относительной
деформации (
;
δ
– перемещение точки приложения силы
Р. На основе понятия относительной
деформации (![]() )
определяют искомое перемещение.
)
определяют искомое перемещение.
Ответ: δ=2 а.
5.24. Найти величину наружного давления q, считая заданными Q, F (рис. 5.20) и коэффициент Пуассона μ, если Δl = 0.

Рекомендации.
При
решении задачи необходимо учесть, что
абсолютная деформация будет равна Δl
=
![]() l1,
где
– относительная деформация.
l1,
где
– относительная деформация.
Величину же , определяют на основе обобщенного закона Гука, для чего составляют схему напряженного состояния малого элемента бруса (рис. 5.21).
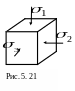
Здесь
![]() ;
;
![]() .
.
Учитывая условие Δl = 0, устанавливают искомое давление.
Ответ:
![]()
