3. Примеры решения задач

3.1. Задачи по теме «Электромагнитные колебания»

Задача 3.1.1. Колебательный контур содержит конденсатор электроемкостью C=8 и катушку индуктивностью =0,5мГн. Каково максимальное напряжение на обкладках конденсатора, если максимальная сила тока =40 мA?

Решение: Запишем закон изменения заряда на конденсаторе контура и тока в катушке индуктивности:

q= (1)

(2)

При этом напряжение на обкладках конденсатора

U= (3)

Из выражения (2) видно, что амплитуда тока

, (4)

где (формула Томсона). (5)

Амплитуда колебания напряжения на конденсаторе, как это следует из (3), равна

= (6)

Максимальное значение заряда на конденсаторе, согласно (4), равно

Если учесть выражение (5), найдем

(7)

Далее подставляя (7) в (6), будем иметь

. (8)

Произведем вычисление:

=4 (В)

Ответ: (В).

Задача 3.1.2. В колебательном контуре происходят вынужденные гармонические колебания. При частотах вынуждающей ЭДС =300 и =600 амплитуда силы тока равна половине своего максимального значения. Определить частоту вынуждающей ЭДС, при которой амплитуда напряжения на обкладках конденсатора максимальна.

Решение: Амплитуда силы тока в контуре при установившихся вынужденных колебаниях

= = (1)

Из выражения (1) видно, что при условии амплитуда тока имеет наибольшее, равно , max= .

При этом соответствующая частота = , где - так называемая собственная частота контура. Следовательно, резонансная частота для тока в контуре , = .

Из условий задачи = = , имеем равенство:

= = . (2)

Из системы (2) имеем уравнения:

3 = (3)

= (4)

Из (4) следует, что либо либо = + , т.е. = . Решение отбрасывается, поскольку оно не удовлетворяет условию задачи. Из второго решения для собственной частоты контура получаем

, (5)

Т.к. = .

Далее равенство (3) перепишем в следующем виде:

3 = =

где - коэффициент затухания.

Итак, для резонансной частоты заряда (напряжения) на конденсаторе имеем:

= = . (6)

Подставив в (5) и (6) значения и =600 , для искомых величин получим:

,

Задача 3.1.3. Колебательный контур содержит катушку индуктивностью R= 3 Ом, а также конденсатор емкостью C= 10нФ. Определить среднюю мощность потребляемую контуром, необходимую для поддержания в нем незатухающих колебаний с амплитудным значением напряжения на конденсаторе =2B.

Решение: При наличии активного сопротивления R полная энергия контура, состоящая из энергии электрического поля, сосредоточенного в конденсаторе, и энергии магнитного поля, сосредоточенного в катушке, непрерывно уменьшается за счет выделения теплоты в соответствии с законом Джоуля-Ленца.

Чтобы поддерживать колебания незатухающими, контур должен получать энергию извне, причем средняя потребляемая мощность равна отношению джоулевой теплоты выделяющейся на сопротивлении R в течении некоторого промежутка времени , к этому промежутку

. (1)

Количество выделившейся теплоты

Q= Rdt . (2)

Очевидно, что характер незатухающих колебаний, а значит и выбор промежутка времени зависят от того, как происходит подача энергии извне. Если предположить, что возникающие незатухающие колебания близки к гармоническим, то промежуток времени следует брать равным периоду колебаний: =T= (3)

Тогда заряд на обкладках конденсатора изменяется по закону

q= , (4)

где . (5)

Дифференцируя по t (4), находим, что сила тока в конуре равна

= - (6)

В выражениях (4) и (6) будем считать, что циклическая частота мало отличается от собственной частоты контура, т.е.

= . (7)

Подставляя выражения (3) и (6) в (2), найдем

= ,

а учитывая, что = , получим

(8)

Подставляя (8) в (1) и учитывая (3), можем найти среднюю за период мощность:

= = (9)

При подстановке (5) и (7) в (9), получим

= = .(10)

Для заданных значений С, , R и средняя мощность:

= =6 (Вт) = 0,6mВт.

Ответ: 0,6mВт.

Задача 3.1.4. Цепь переменного тока состоит из последовательно соединенных катушки , конденсатора С и резистора R. Амплитудное значение суммарного напряжения на катушке и конденсаторе =173 B, а амплитудное значение напряжения на резисторе =100B. Определить сдвиг фаз между током и внешним напряжением.

Решение: Цепь переменного тока представлена на рис.3.1. Из теории вынужденных электромагнитных колебаний известно, что векторная диаграмма сложения амплитуд напряжений на индуктивности, электроемкости и резисторе имеет вид (рис.3.2.)

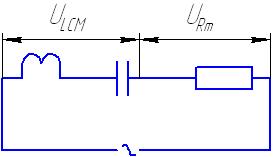
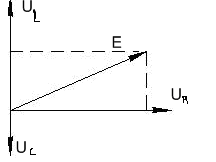
Рис.3.1 Рис.3.2

Здесь = , = , .

Из рис.3.2 следует, что

tg = = . (1)

Подставляя в (1) числовые значения задачи, получим

tg = = = 1,73 , т.е. .

Ответ: .

Задача 3.1.5.Плоский конденсатор с круглыми пластинами заряжается постоянным током в течении времени до напряжения 𝒰. Зазор между пластинами равен d. Проведя между пластинами коаксиальную с ними воображаемую цилиндрическую поверхность, радиус которой r много меньше радиуса пластин, определить:

1. Модуль и направление вектора Пойнтинга в точках поверхности;

2. Количество энергии W, протекающей через поверхность за время . Сравнить W с энергией электрического поля, содержащейся в ограниченном поверхностью объеме V после окончания процесса зарядки.

Решение: Сперва установим зависимость напряженности электрического поля E(t) в зазоре между обкладками конденсатора:

q= t, 0 Напряжение на конденсаторе .Отсюда С= , )t и напряженность поля E= = . При этом электрическое смещение по модулю D= , плотность тока смещения = = .

Рис.3.3

Векторы , и при направлены слева- направо (рис. 3.3).

По теореме о циркуляции вектора по окружности радиуса r, расположенной в плоскости перпендикулярной полю =E , можем написать:

2 H= (1)

Вектор направлен по касательной в каждой точке окружности и в сторону поворота часовой стрелки, если смотришь с лева. Учитывая взаимную ориентацию векторов , и скажем, что вектор Пойнтинга направлен в сторону оси симметрии (внутрь цилиндрического объема).

Поскольку , модуль вектора Пойнтинга S=EH= . (2)

Энергия, поступающая внутрь выделенного цилиндра через его поверхность за промежуток времени

dW=S .

За промежуток времени притекающая энергия W= (3)

Энергия электрического поля в объеме выделенного цилиндра к моменту равна

= V= . (4)

Из (3) и (4) следует, что