
- •Электромагнитные колебания и волны методические указания
- •Предварительные замечания
- •1. Электрические колебания
- •Уравнение колебательного контура
- •Свободные электрические колебания
- •1.3. Затухающие электрические колебания
- •. Вынужденные электрические колебания
- •1.5. Переменный ток
- •2. Электромагнитные волны
- •2.1. Электромагнитное поле. Уравнения Максвелла
- •2.2. Особенности электромагнитных волн
- •2.3. Энергия и поток энергии электромагнитных волн
- •2.4. Давление электромагнитной волны
- •2.5. Импульс электромагнитного поля
- •2.6. Стоячие электромагнитные волны
- •2.7. Испускание электромагнитных волн
- •3. Примеры решения задач
- •3.1. Задачи по теме «Электромагнитные колебания»
- •3.2. Задачи по теме “ Электромагнитные волны”
- •Библиографический список
- •Содержание
- •Электромагнитные колебания и волны методические указания
- •394026 Воронеж, Московский просп., 14
2.5. Импульс электромагнитного поля
Электромагнитная волна переносит
энергию с плотностью потока ![]() и, падая на тело, оказывает на него
давление. Следовательно, электромагнитное
поле (волна) обладает импульсом.
Получим
выражение для объемной плотности
и, падая на тело, оказывает на него
давление. Следовательно, электромагнитное
поле (волна) обладает импульсом.
Получим
выражение для объемной плотности ![]() электромагнитной волны в
вакууме. В пространстве плоской волны
в направлении ее распространения выделим
цилиндрический элемент объемом
электромагнитной волны в
вакууме. В пространстве плоской волны
в направлении ее распространения выделим
цилиндрический элемент объемом ![]() где
– площадь сечения,
где
– площадь сечения, ![]() - расстояние между выбранными фронтами
волны. В пределах выделенного элемента
объема во всех его точках плотность
электромагнитной энергии
- расстояние между выбранными фронтами
волны. В пределах выделенного элемента
объема во всех его точках плотность
электромагнитной энергии
![]() практически одинакова и, следовательно,
энергия, заключенная в объеме
практически одинакова и, следовательно,
энергия, заключенная в объеме ![]() равна
равна ![]() .
Масса покоя квантов электромагнитного
поля равна нулю. Однако электромагнитному
полю в некотором объеме можно сопоставить
релятивистскую массу
.
Масса покоя квантов электромагнитного
поля равна нулю. Однако электромагнитному
полю в некотором объеме можно сопоставить
релятивистскую массу ![]() .
В рассматриваемом случае релятивистская
масса выделенного элемента поля волны
равна
.
В рассматриваемом случае релятивистская
масса выделенного элемента поля волны
равна![]() При скорости распространения волны
равной
При скорости распространения волны
равной![]() «
«![]() »
соответствующий импульс по модулю
»
соответствующий импульс по модулю
![]() .При
этом объемная плотность импульса по
абсолютному значению:
.При
этом объемная плотность импульса по
абсолютному значению:
![]()
Если учесть, что ![]() (смотреть формулу 2.33), получим
(смотреть формулу 2.33), получим ![]() .
Направления
.
Направления ![]() совпадают, поэтому можно написать
совпадают, поэтому можно написать ![]() (2.39).
(2.39).
Итак, для объемной плотности импульса электромагнитной волны имеем:
![]()
2.6. Стоячие электромагнитные волны
Стоячие электромагнитные волны возникают
при наложении двух распространяющихся
в противоположенных направлениях волн
одинаковой частоты, амплитуды и
поляризации. Такая картина получается,
в частности, при полном отражении волны
от границы. Рассмотрим случай нормального
падения плоской монохроматической и
линейно-поляризованной волны на хорошо
отражающую поверхность с относительным
показателем преломления ![]() Задача будет состоять в выяснении
структуры стоячей волны.
Задача будет состоять в выяснении
структуры стоячей волны.
П
Рис. 2.5![]() ,
направление поляризации определим осью
,
направление поляризации определим осью
![]() (рис. 2.5). Начало отсчета расстояний
на оси
(рис. 2.5). Начало отсчета расстояний
на оси 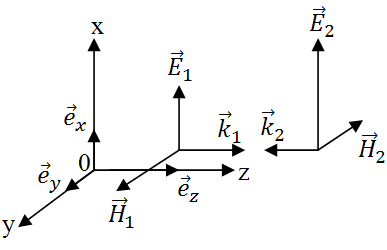 выберем в точке, где колебания напряженности
электрического поля обеих волн происходят
в одинаковой фазе, а начало отсчета
времени в тот момент, когда эти
напряженности в начале координат
достигают максимума. При этом выражения
выберем в точке, где колебания напряженности
электрического поля обеих волн происходят
в одинаковой фазе, а начало отсчета
времени в тот момент, когда эти
напряженности в начале координат
достигают максимума. При этом выражения
![]() прямой волны принимают особенно простой
вид:
прямой волны принимают особенно простой
вид:
![]()
Для волны распространяющейся навстречу, мы должны написать:
![]()
Здесь учтено, что векторы![]() в каждой из волн должны образовывать
правую тройку векторов (рис. 2.5). Путем
сложения найдем результирующее
электромагнитное поле:
в каждой из волн должны образовывать
правую тройку векторов (рис. 2.5). Путем
сложения найдем результирующее
электромагнитное поле:
![]()
![]()
Из полученных формул видно, что вектор
результирующей волны в каждой точке
совершает гармоническое колебание
вдоль оси
с частотой
![]() ,
причем амплитуда колебаний в зависимости
от
изменяется от максимального значения
,
причем амплитуда колебаний в зависимости
от
изменяется от максимального значения
![]() в плоскостях
в плоскостях ![]() называемых
пучностями электрического поля, до ноля
в плоскостях
называемых
пучностями электрического поля, до ноля
в плоскостях ![]() ,
называемых узлами. Фаза колебаний
во всех точках между соседними узлами
одинакова, а колебания по разные стороны
узла происходят в противофазе.
,
называемых узлами. Фаза колебаний
во всех точках между соседними узлами
одинакова, а колебания по разные стороны
узла происходят в противофазе.
Колебания магнитного поля происходят в направлении, перпендикулярном , и также представляют собой стоячую волну. Однако пучности и узлы стоячей волны магнитного поля сдвинуты вдоль оси на четверть длины волны по отношению к пучности и узлам электрического поля. Колебания магнитного поля отстают во времени на четверть периода от колебаний электрического поля.
Стоячая волна, как и бегущая, могут иметь иной вид поляризации. Например, стоячая волна возникает при отражении циркулярнополяризованной волны от идеального плоского зеркала.
