
- •Тематические тесты по математике
- •М.Ю. Глазкова, в.Н. Колпачев, т.Г. Святская, в.А. Попова, е.И.Ханкин
- •1. Степени с рациональными показателями. Корни. Вариант 1.1.
- •Вариант 1.2.
- •Вариант 1.3.
- •Вариант 1.4.
- •Вариант 1.5.
- •Вариант 1.6.
- •Вариант 1.7.
- •Вариант 1.8.
- •Вариант 1.9.
- •Вариант 1.10.
- •2. Рациональные уравнения Вариант 2.1.
- •Вариант 2.2.
- •Вариант 2.3.
- •Вариант 2.4.
- •Вариант 2.5.
- •Вариант 2.6.
- •Вариант 2.7.
- •Вариант 2.8.
- •Вариант 2.9.
- •Вариант 2.10.
- •3. Уравнения, содержащие неизвестное под знаком модуля. Вариант 3.1
- •Вариант 3.2
- •Вариант 3.3
- •Вариант 3.4
- •Вариант 3.5
- •Вариант 3.6
- •Вариант 3.7
- •Вариант 3.8
- •Вариант 3.9
- •Вариант 3.10
- •4. Иррациональные уравнения Вариант 4.1
- •Вариант 4.2
- •Вариант 4.3
- •Вариант 4.4
- •Вариант 4.5
- •Вариант 4.6
- •Вариант 4.7
- •Вариант 4.8
- •Вариант 4.9
- •Вариант 4.10
- •5. Неравенства, содержащие неизвестные под знаком модуля. Иррациональные неравенства. Вариант 5.1.
- •Вариант 5.2.
- •Вариант 5.3.
- •Вариант 5.4.
- •Вариант 5.5.
- •Вариант 5.6.
- •Вариант 5.7.
- •Вариант 5.8.
- •Вариант 5.9.
- •Вариант 5.10.
- •6. Системы алгебраических уравнений. Рациональные неравенства Вариант 6.1
- •Вариант 6.2
- •Вариант 6.3
- •Вариант 6.4
- •Вариант 6.5
- •Вариант 6.6
- •Вариант 6.7
- •Вариант 6.8
- •Вариант 6.9
- •Вариант 6.10
- •7. Преобразование тригонометрических выражений. Вариант 7.1
- •Вариант 7.2
- •Вариант 7.3
- •Вариант 7.4
- •Вариант 7.5
- •Вариант 7.6
- •Вариант 7.7
- •Вариант 7.8
- •Вариант 7.9
- •Вариант 7.10
- •8. Тригонометрические уравнения Вариант 8.1
- •Вариант 8.2
- •Вариант 8.3
- •Вариант № 8.4
- •Вариант № 8.5
- •Вариант № 8.6
- •Вариант № 8.7
- •Вариант № 8.8
- •Вариант № 8.9
- •Вариант № 8.10
- •9. Показательные уравнения. Показательные неравенства. Вариант 9.1.
- •Вариант 9.2.
- •Вариант 9.3.
- •Вариант 9.4.
- •Вариант 9.5.
- •Вариант 9.6.
- •Вариант 9.7.
- •Вариант 9.8.
- •Вариант 9.9.
- •Вариант 9.10.
- •10. Логарифмические уравнения и неравенства Вариант № 10.1
- •Вариант № 10.2
- •Вариант №10.3
- •Вариант №10.4
- •Вариант №10.5
- •Вариант №10.6
- •Вариант № 10.7
- •Вариант 10.8
- •Вариант 10.9
- •Вариант 10.10
- •11. Логарифмические неравенства и системы показательных и логарифмических уравнений и неравенств. Вариант 11.1
- •Вариант 11.2
- •Вариант 11.3
- •Вариант 11.4
- •Вариант 11.5
- •Вариант 11.6
- •Вариант 11.7
- •Вариант 11.8
- •Вариант 11.9
- •Вариант 11.10
- •12. Текстовые задачи Вариант 12.1
- •Вариант 12.2
- •Вариант 12.3
- •Вариант 12.4
- •Вариант 12.5
- •Вариант 12.6
- •Вариант 12.7
- •Вариант 12.8
- •Вариант 12.9
- •Вариант 12.10
- •13. Начала анализа Вариант 13 .1
- •Вариант 13 .2
- •Вариант 13.3
- •Вариант 13 .4
- •Вариант 13 .5
- •Вариант 13 .6
- •Вариант 13.7
- •Вариант 13 .8
- •Вариант 13 .9
- •Вариант 13 .10
- •14. Геометрия Вариант 14.1
- •Вариант 14.2
- •Вариант 14.3
- •Вариант 14.4
- •Вариант 14.5
- •Вариант 14.6
- •Вариант 14.7
- •Вариант 14.8
- •Вариант 14.9
- •Вариант 14.10
- •15. Задачи с параметрами Вариант 15.1
- •Вариант 15 .2
- •Вариант 15.3
- •Вариант 15.4
- •Вариант 15.5
- •Вариант `15.6
- •Вариант 15.7
- •Вариант 15.8
- •Вариант 15.9
- •Вариант 15.10
- •Литература
- •Тематические тесты по математике
- •394006 Воронеж, ул. 20-летия Октября, 84
Вариант 2.7.
А1.
Корень уравнения
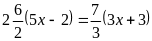 равен
равен
1)
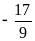 ; 2)
; 2)
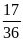 ; 3)
; 3)
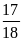 ; 4)
; 4)
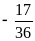 .
.
А2.
Корень уравнения
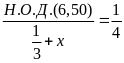 равен
равен
1)
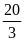 ; 2)
; 2)
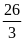 ; 3)
; 3)
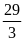 ; 4)
; 4)
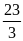 .
.
А3.
Сумма корней уравнения
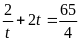 равна
равна
1)
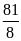 ; 2)
; 2)
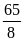 ; 3)
; 3)
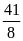 ; 4)
; 4)
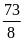 .
.
А4.
Сумма корней уравнения
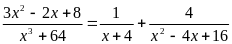 равна
равна
1) -1; 2) 2; 3) 1; 4) 0.
А5.
Число действительных корней уравнения
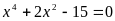 равно
равно
1) 2; 2) 4; 3) 3; 4) 1.
В1.
Если k – число корней
уравнения
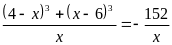 ,
а x0 – его
положительный корень, то число k
∙ x0 равно
,
а x0 – его
положительный корень, то число k
∙ x0 равно
В2.
Наименьший корень уравнения
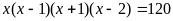 равен
равен
В3.
Сумма действительных корней уравнения
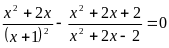 равна
равна
В4.
Корень уравнения (или их произведение,
если корней несколько)
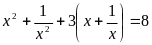 равен
равен
В5.
Наибольший корень уравнения
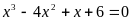 равен
равен
Вариант 2.8.
А1.
Корень уравнения
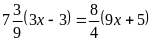 равен
равен
1) -8; 2) 4; 3) -4; 4) 8.
А2.
Корень уравнения
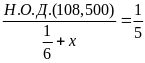 равен
равен
1)
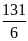 ; 2)
; 2)
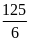 ; 3)
; 3)
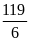 ; 4)
; 4)
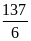 .
.
А3.
Сумма корней уравнения
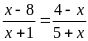 равна
равна
1) 6; 2) 7; 3) 2; 4) 3.
А4.
Сумма корней уравнения
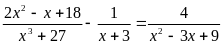 равна
равна
1) 0; 2) -1; 3) 5; 4) 2.
А5.
Корень уравнения (или произведение
корней, если их несколько), принадлежит
промежутку
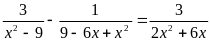
1) (0, 2]; 2) (2, 3); 3) [4, 5]; 4) [-1, 0).
В1.
Если k – число корней
уравнения
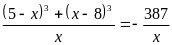 ,
а x0 – его
положительный корень, то число k
∙ x0 равно
,
а x0 – его
положительный корень, то число k
∙ x0 равно
В2.
Сумма корней уравнения
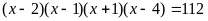 равна
равна
В3.
Сумма корней уравнения
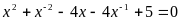 равна
равна
В4.
Произведение корней уравнения
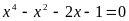 равно
равно
В5.
Корень уравнения (или наибольший из
них, если корней несколько)
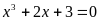 равен
равен
Вариант 2.9.
А1.
Корень уравнения
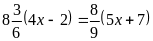 равен
равен
1)
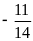 ; 2)
; 2)
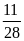 ; 3)
; 3)
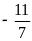 ; 4)
; 4)
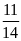 .
.
А2.
Корень уравнения
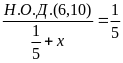 равен
равен
1)
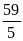 ; 2)
; 2)
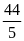 ; 3)
; 3)
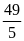 ; 4)
; 4)
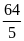 .
.
А3.
Сумма корней уравнения
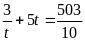 равна
равна
1)
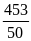 ; 2)
; 2)
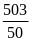 ; 3)
; 3)
 ; 4)
; 4)
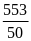 .
.
А4.
Сумма корней уравнения
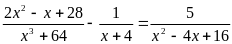 равна
равна
1) 2; 2) -2; 3) 0; 4) -1.
А5.
Произведение корней уравнения
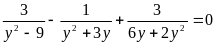 принадлежит промежутку
принадлежит промежутку
1) [-1, 1]; 2) (2, 3]; 3) [-2, 0]; 4) [1, 5].
В1.
Если k – число корней
уравнения
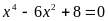 ,
а x0 – его
наибольший корень, то число k
∙ x0 равно
,
а x0 – его
наибольший корень, то число k
∙ x0 равно
В2.
Сумма иррациональных корней уравнения
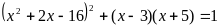 равна
равна
В3.
Сумма корней уравнения
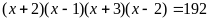 равна
равна
В4.
Наименьший корень уравнения
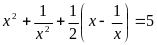 равен
равен
В5.
Произведение корней уравнения
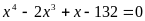 равно
равно
Вариант 2.10.
А1.
Корень уравнения
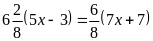 равен
равен
1)
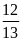 ; 2)
; 2)
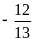 ; 3)
; 3)
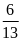 ; 4)
; 4)
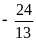 .
.
А2.
Корень уравнения
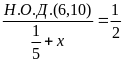 равен
равен
1)
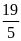 ; 2)
; 2)
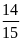 ; 3)
; 3)
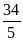 ; 4)
; 4)
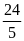 .
.
А3.
Сумма корней уравнения
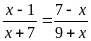 равна
равна
1) -1; 2) -4; 3) 2; 4) -5.
А4.
Корень уравнения
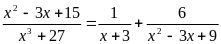 принадлежит промежутку
принадлежит промежутку
1) (0, 3); 2) [-10, -3); 3) [-3, -1); 4) (-1, 0].
А5.
Корень уравнения
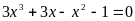 принадлежит промежутку
принадлежит промежутку
1)
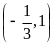 ; 2)
( -∞, -5); 3) другой промежуток; 4)
; 2)
( -∞, -5); 3) другой промежуток; 4)
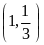 .
.
В1.
Если k – число корней
уравнения
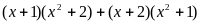 ,
а x0 – его
отрицательный корень, то число k
∙ x0 равно
,
а x0 – его
отрицательный корень, то число k
∙ x0 равно
В2. Сумма корней уравнения равна
В3.
Сумма корней уравнения
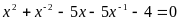 равна
равна
В4.
Корень уравнения (или наименьший из
корней, если их несколько)
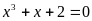 равен
равен
В5.
Корень уравнения (или произведение
корней, если их несколько)
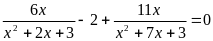 равен
равен
