
- •Тематические тесты по математике
- •М.Ю. Глазкова, в.Н. Колпачев, т.Г. Святская, в.А. Попова, е.И.Ханкин
- •1. Степени с рациональными показателями. Корни. Вариант 1.1.
- •Вариант 1.2.
- •Вариант 1.3.
- •Вариант 1.4.
- •Вариант 1.5.
- •Вариант 1.6.
- •Вариант 1.7.
- •Вариант 1.8.
- •Вариант 1.9.
- •Вариант 1.10.
- •2. Рациональные уравнения Вариант 2.1.
- •Вариант 2.2.
- •Вариант 2.3.
- •Вариант 2.4.
- •Вариант 2.5.
- •Вариант 2.6.
- •Вариант 2.7.
- •Вариант 2.8.
- •Вариант 2.9.
- •Вариант 2.10.
- •3. Уравнения, содержащие неизвестное под знаком модуля. Вариант 3.1
- •Вариант 3.2
- •Вариант 3.3
- •Вариант 3.4
- •Вариант 3.5
- •Вариант 3.6
- •Вариант 3.7
- •Вариант 3.8
- •Вариант 3.9
- •Вариант 3.10
- •4. Иррациональные уравнения Вариант 4.1
- •Вариант 4.2
- •Вариант 4.3
- •Вариант 4.4
- •Вариант 4.5
- •Вариант 4.6
- •Вариант 4.7
- •Вариант 4.8
- •Вариант 4.9
- •Вариант 4.10
- •5. Неравенства, содержащие неизвестные под знаком модуля. Иррациональные неравенства. Вариант 5.1.
- •Вариант 5.2.
- •Вариант 5.3.
- •Вариант 5.4.
- •Вариант 5.5.
- •Вариант 5.6.
- •Вариант 5.7.
- •Вариант 5.8.
- •Вариант 5.9.
- •Вариант 5.10.
- •6. Системы алгебраических уравнений. Рациональные неравенства Вариант 6.1
- •Вариант 6.2
- •Вариант 6.3
- •Вариант 6.4
- •Вариант 6.5
- •Вариант 6.6
- •Вариант 6.7
- •Вариант 6.8
- •Вариант 6.9
- •Вариант 6.10
- •7. Преобразование тригонометрических выражений. Вариант 7.1
- •Вариант 7.2
- •Вариант 7.3
- •Вариант 7.4
- •Вариант 7.5
- •Вариант 7.6
- •Вариант 7.7
- •Вариант 7.8
- •Вариант 7.9
- •Вариант 7.10
- •8. Тригонометрические уравнения Вариант 8.1
- •Вариант 8.2
- •Вариант 8.3
- •Вариант № 8.4
- •Вариант № 8.5
- •Вариант № 8.6
- •Вариант № 8.7
- •Вариант № 8.8
- •Вариант № 8.9
- •Вариант № 8.10
- •9. Показательные уравнения. Показательные неравенства. Вариант 9.1.
- •Вариант 9.2.
- •Вариант 9.3.
- •Вариант 9.4.
- •Вариант 9.5.
- •Вариант 9.6.
- •Вариант 9.7.
- •Вариант 9.8.
- •Вариант 9.9.
- •Вариант 9.10.
- •10. Логарифмические уравнения и неравенства Вариант № 10.1
- •Вариант № 10.2
- •Вариант №10.3
- •Вариант №10.4
- •Вариант №10.5
- •Вариант №10.6
- •Вариант № 10.7
- •Вариант 10.8
- •Вариант 10.9
- •Вариант 10.10
- •11. Логарифмические неравенства и системы показательных и логарифмических уравнений и неравенств. Вариант 11.1
- •Вариант 11.2
- •Вариант 11.3
- •Вариант 11.4
- •Вариант 11.5
- •Вариант 11.6
- •Вариант 11.7
- •Вариант 11.8
- •Вариант 11.9
- •Вариант 11.10
- •12. Текстовые задачи Вариант 12.1
- •Вариант 12.2
- •Вариант 12.3
- •Вариант 12.4
- •Вариант 12.5
- •Вариант 12.6
- •Вариант 12.7
- •Вариант 12.8
- •Вариант 12.9
- •Вариант 12.10
- •13. Начала анализа Вариант 13 .1
- •Вариант 13 .2
- •Вариант 13.3
- •Вариант 13 .4
- •Вариант 13 .5
- •Вариант 13 .6
- •Вариант 13.7
- •Вариант 13 .8
- •Вариант 13 .9
- •Вариант 13 .10
- •14. Геометрия Вариант 14.1
- •Вариант 14.2
- •Вариант 14.3
- •Вариант 14.4
- •Вариант 14.5
- •Вариант 14.6
- •Вариант 14.7
- •Вариант 14.8
- •Вариант 14.9
- •Вариант 14.10
- •15. Задачи с параметрами Вариант 15.1
- •Вариант 15 .2
- •Вариант 15.3
- •Вариант 15.4
- •Вариант 15.5
- •Вариант `15.6
- •Вариант 15.7
- •Вариант 15.8
- •Вариант 15.9
- •Вариант 15.10
- •Литература
- •Тематические тесты по математике
- •394006 Воронеж, ул. 20-летия Октября, 84
Вариант 9.9.
А1.
Корень уравнения
 равен
равен
1) ; 2) -16; 3) 16; 4) 17.
А2.
Абсцисса точки пересечения графиков
функций
и
 равна
равна
1)
-3; 2)
; 3)
 ; 4)
.
; 4)
.
А3. Если x0 - корень уравнения , тогда выражение 3 x0 + 8 равно
1) 7; 2) 5; 3) 6; 4) 8.
А4.
Решением неравенства
 является промежуток
является промежуток
1) (-∞; -2); 2) [2; +∞); 3) (2; +∞); 4) (-∞; -2].
А5.
Сумма целых корней уравнения
 равна
равна
1) -3; 2) 2; 3) -2; 4) 1.
В1.
Сумма целых решений неравенства
 равна
равна
В2.
Наибольшее решение неравенства
 равно
равно
В3.
Корень уравнения
 равен
равен
В4.
Число целых решений неравенства
 ,
принадлежащих отрезку
,
принадлежащих отрезку
[-1; 3], равно
В5.
Наименьшее целое решение неравенства
 равно
равно
Вариант 9.10.
А1.
Корень уравнения
 равен
равен
1) ; 2) -12; 3) ; 4) 12.
А2.
Абсцисса точки пересечения графиков
функций
и
 равна
равна
1)
; 2)
 ; 3)
; 4)
-2.
; 3)
; 4)
-2.
А3.
Если x0 - корень
уравнения
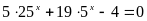 ,
тогда выражение 3 x0
+ 6 равно
,
тогда выражение 3 x0
+ 6 равно
1) 3; 2) 6; 3) 5; 4) 4.
А4.
Сумма корней уравнения
 равна
равна
1)
3; 2)
 ; 3)
; 3)
 ; 4)
2.
; 4)
2.
А5.
Решением неравенства
 является промежуток
является промежуток
1) (-∞; -3); 2) (-∞; -3]; 3) (-3; +∞); 4) [-3; +∞).
В1.
Корень уравнения
 равен
равен
В2.
Сумма целых решений неравенства
 равна
равна
В3.
Число целых решений неравенства
 равно
равно
В4.
Сумма целых решений неравенства
 ,
принадлежащих отрезку
,
принадлежащих отрезку
[-5; 3], равно
В5.
Наибольшее целое решение неравенства
 равно
равно
10. Логарифмические уравнения и неравенства Вариант № 10.1
А1. Упростите выражение

1) 36; 2) 1; 3) 4; 4) 2;
А2. Если

 ,
то значение выражения log
,
то значение выражения log
 равно
равно
1)4/3 а -10/9; 2) 4/3 а + 8/9; 3) 4/3 а - 19/9; 4) 4/3 а +17/9
А3. Если x -корень
уравнения log
-корень
уравнения log x
+ log
x
+ log x
+ log
x
+ log x
=
x
=
 ,
то значение выражения
,
то значение выражения
x(x- )
) +1
равно
+1
равно
1) 12; 2) 7; 3) 10; 4) 8
А4. Произведение корней уравнения log
x
- log 2=1,5
равно
2=1,5
равно
1)2
+1
2)2
3)2
-1
4)

А5. Если x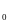 - наименьший корень уравнения
- наименьший корень уравнения
 ,
,
То значение
выражения
 равно
равно
1) 193/64; 2) 129/64; 3) 257/64; 4) 65/64; .
В1. Произведение
корней уравнения 2 равно
равно
В2.
Результат вычисления
 равен
равен
B3. Корень уравнения log x=6log 8-3log 4 равен
B4.
Корень уравнения log (
( -
- +
+ )=0,5log
(x+7)
равен
)=0,5log
(x+7)
равен
B5.
Если
-
корень уравнения
 то значение выражения
то значение выражения
 равно
равно
Вариант № 10.2
А1. Результат упрощения выражения
log 121+2
log
(
121+2
log
( )
равен
)
равен
1) 81 2) 4 3) 1 4) 2
А2. Если log
 = a, то значение выражения
log
= a, то значение выражения
log
 равно
равно
1)7/6a+16/9; 2)7/6a+7/9; 3)7/6a-11/9; 4)7/6a-20/9;
А3. Если
x
-корень
уравнения log
x+log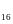 x+log
x+log x=
x= ,
то значение выражения
,
то значение выражения
x/(x-224)+1 равно
1)7 2)11 3)9 4)6
A4. Произведение корней уравнения log x-log 5=1,5 равно
1)1/25 2)5
+1
3)5
4)
2)5
+1
3)5
4)
A5. Если x -наименьший корень уравнения
 то значении выражения x
(1+
то значении выражения x
(1+ )
равно
)
равно
1)433/216 2)865/216 3)1081/216 4)217/216
B1.
Произведение корней уравнения 2
log x-log
(14x-49)=0
равно
x-log
(14x-49)=0
равно
B2.
Результат вычисления
 равен
равен
B3. Корень уравнения log x=2 log 9-2 log 3 равен
B4. Корень уравнения
log
( -
- +
+ )=0,5
log
(6+x)
равен
)=0,5
log
(6+x)
равен
В5. Если x -корень уравнения log log log x=0, то значение выражения x (x -2) равно
