
- •230100 «Информатика и вычислительная техника»
- •Часть 1
- •1.Основные определения
- •2. Линии и поверхности уровня
- •4. Предел и непрерывность функции
- •5. Частные производные функции нескольких
- •6. Геометрический смысл частных
- •10. Геометрический смысл полного
- •11. Производные сложных функций
- •12. Полный дифференциал сложной функции
- •13. Производная от функции, заданной неявно
- •14. Частные производные различных порядков
- •230100 «Информатика и вычислительная техника»
- •Часть 1
- •394026 Воронеж, Московский просп., 14
12. Полный дифференциал сложной функции
Пусть
.
Найдем полный дифференциал сложной
функции:
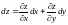 ,
но
,
но
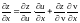 ,
,
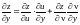 ,
поэтому
,
поэтому
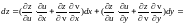
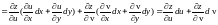
или
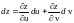 .
.
Мы показали, что выражения полного дифференциала
функции
нескольких переменных (дифференциала
первого порядка) имеют одинаковый вид,
как в случае если
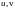 - независимые переменные так и в случае,
если
- независимые переменные так и в случае,
если
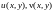 есть функции независимых переменных.
Это свойство первого дифференциала
сохранять форму, называется инвариантностью
формы первого дифференциала.
есть функции независимых переменных.
Это свойство первого дифференциала
сохранять форму, называется инвариантностью
формы первого дифференциала.
Задачи для самостоятельной работы
1. Найти
,
если
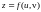 :
:
1.1
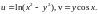
1.2.
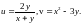
2. Найти
,
если
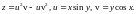
3. Выразить
через
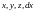 и
и
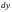 ,
если:
,
если:
3.1.
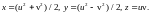
3.2.
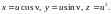
3.3.
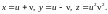
13. Производная от функции, заданной неявно
Теорема.
Пусть непрерывная функция
от
задается неявно уравнением
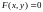 ,
где
,
где
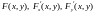 -
непрерывные функции в некоторой области,
содержащей точку
-
непрерывные функции в некоторой области,
содержащей точку
, координаты которой удовлетворяют уравнению
,
кроме того,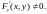 Тогда
Тогда
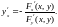
Доказательство.
Дадим
приращение
,
тогда
получит приращение
и
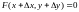 .
Следовательно,
.
Следовательно,
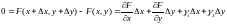 .
.
Выразим из последнего равенства отношение приращения функции к приращению аргумента :
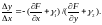
Переходя к пределу при , получим
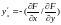 .
.
Пример. Найти
производную функции
,
заданной неявно уравнением
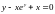 .
.
Решение.
Обозначим
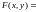
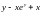 .
Вычислим частные производные
.
Вычислим частные производные
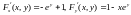 ,
тогда
,
тогда
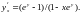
Пример.
Найти
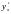 ,
если
,
если
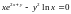 .
.
Решение.
Обозначим
левую часть уравнения через F(x;
y).
Тогда
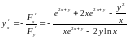 .
.
Рассмотрим уравнение вида . Если каждой паре чисел из некоторой области соответствует одно или несколько значений , удовлетворяющих уравнению. Тогда это уравнение неявно определяет одну или несколько однозначных функций от , частные производные неявной функции имеют вид:
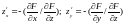 при
при
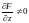 .
.
Пример.
Найти
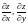 ,
если
,
если
 .
.
Решение. Обозначим через F(x; y; z) левую часть уравнения. Имеем
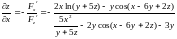 ,
,
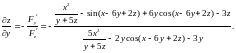
Задачи для самостоятельной работы
1. Найти производную функции , заданной неявно уравнениями:
1.1.
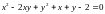 в точке
в точке
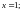
1.2.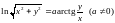 .
.
1.3.
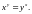 1.4.
1.4.
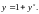
1.5.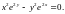 1.6.
1.6.
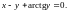
1.7.
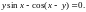
1.8.
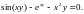
1.9.
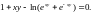
1.10.
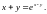
2. Найти
частные производные
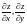 функции
,
заданной неявно уравнениями:
функции
,
заданной неявно уравнениями:
2.1.
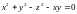 в точке
в точке
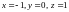 ;
;
2.2.
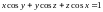 .
.
2.3.
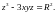
2.4.
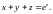
Ответы: 1.1.
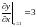 или -1; 1.2.
или -1; 1.2.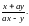 2.1.
2.1.
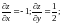
2.2.
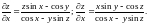
14. Частные производные различных порядков
Пусть . Тогда частные производные также являются функциями от переменных . В некоторых
случаях для этих функций снова существуют частные производные, называемые частными производными второго порядка, очевидно, что эти производные четырех видов:
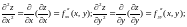
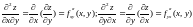 .
.
Две последние производные называются смешанными производными второго порядка.
Производные второго порядка можно снова
дифференцировать как по , так и по . Получим частные производные третьего порядка:
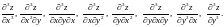
Частная
производная
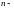 го
порядка
го
порядка
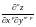 получается, если функцию
получается, если функцию
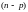 раз
продифференцировать по переменной
,
а затем
раз
продифференцировать по переменной
,
а затем
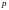 раз по
.
раз по
.
Примеры.
1.
Найти все частные производные второго
порядка от функции
=
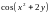 .
.
Решение. Запишем сначала частные производные по и по .
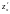 = – 2
= – 2
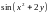 ,
,
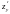 = – 2
.
= – 2
.
Найдем теперь частные производные второго порядка.
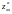 =
=
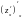 =
=
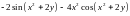 ,
,
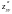 =
=
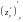 =
=
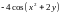 ,
,
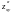 =
=
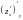 =
=
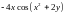 ,
,
2.
Найти частные производные второго
порядка функции
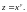
Решение.
Сначала находим частные производные
первого порядка
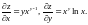 Затем, вычисляя частные производные от
частных производных первого порядка,
получаем частные производные второго
порядка данной функции
Затем, вычисляя частные производные от
частных производных первого порядка,
получаем частные производные второго
порядка данной функции
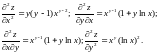
Заметим, что в рассмотренном
примере
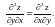
3
.
Найти
все частные производные 2-го порядка
функции
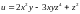 .
Найти
.
Найти
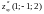 .
.
Решение.
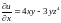 ,
,
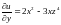 ,
,
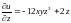 ,
,
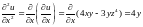 ;
;
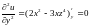 ;
;
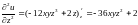 ;
;
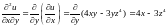 ;
;
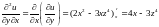 ;
;
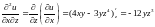 ;
;
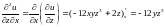 ;
;
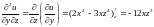 ;
;
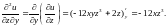
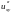 (1;
-1; 2) = 4 - 324
= 4 – 48 = - 44.
(1;
-1; 2) = 4 - 324
= 4 – 48 = - 44.
4. Найти
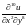 ,
если
,
если
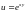 .
.
Решение. Найдем сначала
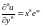 .
Вычисляя теперь по
.
Вычисляя теперь по
формуле Лейбница вторую
производную по
от
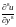 ,
получаем:
=
,
получаем:
=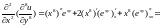
=
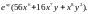
5.
Показать,
что функция
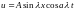 удовлетворяет уравнению колебания
струны
удовлетворяет уравнению колебания
струны
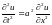 .
.
Решение.
Имеем ;
;
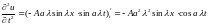 ;
;
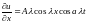 ;
;
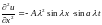 .
.
Сравнивая
полученные выражения, видим, что
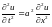 .
.
Возникает
естественный вопрос: зависят ли частные
производные высших порядков от порядка
дифференцирования (в примере 2 мы видели,
что
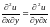 ,
,
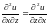 ,
,
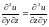 ).
Оказывается, что, вообще говоря, смешанные
производные зависят от порядка
дифференцирования. Однако справедливо
следующее утверждение.
).
Оказывается, что, вообще говоря, смешанные
производные зависят от порядка
дифференцирования. Однако справедливо
следующее утверждение.
Теорема. Если все входящие в вычисления частные производные, рассматриваемые как функции своих независимых переменных, непрерывны, то результат частного дифференцирования не зависит от последовательности дифференцирования.
Например, если
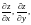
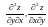 непрерывны, то
непрерывны, то
Задачи для самостоятельной работы
1.Найти частные производные заданных функций до второго порядка включительно:
1.1.
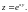 1.2.
1.2.
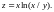 1.3.
1.3.
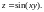
1.4.
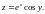 1.5.
1.5.
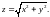 1.6.
1.6.
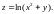
1.7.
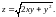 1.8.
1.8.
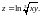 1.9.
1.9.
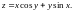
1.10.
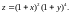
2. Найти частные производные указанного порядка:
2.1.
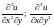 ,
если
,
если
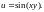
2.2.
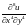 ,
если
,
если
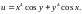
2.3.
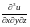 ,
если
,
если
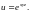 2.4.
2.4.
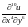 ,
если
,
если
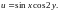 2.5.
2.5.
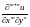 ,
если
,
если
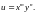 2.6.
2.6.
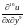 ,
если
,
если
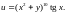 2.7.
,
если
2.7.
,
если
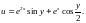
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Пискунов Н.С. Дифференциальное и интегральное исчисления/ Н.С. Пискунов.- М.: Наука, 2001. Т.1.- 250 с.
2.Мантуров О.В. Курс высшей математики/ Мантуров О.В., Матвеев Н.М.- М.: Высш. Шк.,1986.480 с.
3.Сборник задач по математике для втузов. Ч.1. Линейная
алгебра и основы математического анализа. Под ред.
А.В. Ефимова, Б.П.Демидовича.М.:Наука.1993.480 с.
4.Бутузов В.Ф. Математический анализ в вопросах и задачах. Функции нескольких переменных/ Бутузов В.Ф., Крутицкая Н.Ч., Медведев Г.Н., Шишкин А.А.- М.: Высш. Шк., 1988. 288с.
5. Зимина О.В. Высшая математика/ О.В. Зимина, А.И. Кириллов, Т.А. Сальникова.- М.: Физматлит, 2005.-368 с.
6. Рябушко А.П. Индивидуальные задания по высшей математике: учеб. пособие. В 4 ч. Ч.2. Комплексные числа. Неопределенные и определенные интегралы. Функции нескольких переменных. Обыкновенные дифференциальные уравнения/ А.П. Рябушко [и др.]. Минск:Выш. шк., 2007.-396 с.
7. Лунгу К.Н. Сборник задач по высшей математике. 1 курс/Лунгу К.Н., Письменный Д.Т. Федин С.Н., Шевченко Ю.А.-М.: Рольф, 2001.-576 с.
СОДЕРЖАНИЕ
Введение………………………………………………………….1
1. Основные определения…..…………………………… ..1
2. Линии и поверхности уровня………………………… 5
3. Частное и полное приращение функции……………… 6
4. Предел и непрерывность функции нескольких
переменных……………………………………………………… 7
5. Частные производные функции нескольких переменных…………………………………………………………….....14
6. Геометрический смысл частных производных ……...17
7. Дифференциальные операции первого порядка в скалярных и векторных полях……..…………………..………….18
8. Полный дифференциал функции нескольких
переменных……………………….…………………………. ...29
9. Применение полного дифференциала к
приближенным вычислениям……………………………….…32
10.Геометрический смысл полного дифференциала. Касательная плоскость и нормаль к поверхности …………….. 33
11. Производные сложных функций………..………... 37
12. Дифференциал сложной функции…………..…….. .41
13. Производные функций, заданных неявно ...……… 43
14. Частные производные различных порядков…….... 45
БИБЛИОГРАФИЧЕСКИЙ СПИСОК…………………….…50
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
для организации самостоятельной работы
по изучению раздела «Функции нескольких переменных»
курса «Математический анализ»
для студентов по направлению подготовки бакалавров
