- •230100 «Информатика и вычислительная техника»
- •Часть 1
- •1.Основные определения
- •2. Линии и поверхности уровня
- •4. Предел и непрерывность функции
- •5. Частные производные функции нескольких
- •6. Геометрический смысл частных
- •10. Геометрический смысл полного
- •11. Производные сложных функций
- •12. Полный дифференциал сложной функции
- •13. Производная от функции, заданной неявно
- •14. Частные производные различных порядков
- •230100 «Информатика и вычислительная техника»
- •Часть 1
- •394026 Воронеж, Московский просп., 14
10. Геометрический смысл полного
ДИФФЕРЕНЦИАЛА КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К
ПОВЕРХНОСТИ
Подобно тому, как дифференциал функции одной переменной является приращением ординаты касательной, полный дифференциал функции двух переменных есть приращение аппликаты касательной плоскости.
Пусть функция
имеет
в точке
частные производные первого порядка.
На поверхности
возьмем три точки
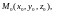
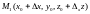 ,
,
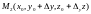 и составим уравнение плоскости, проходящей
через эти точки:
и составим уравнение плоскости, проходящей
через эти точки:
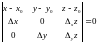 ,
,
или
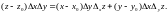 Считая
Считая
 ,
разделим левую и правую части уравнения
на
,
разделим левую и правую части уравнения
на
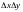 ,
получим
,
получим
 Переходя
Переходя
к пределу при
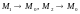 ,
то есть
,
найдем
,
то есть
,
найдем
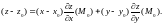
Если функция
дифференцируема, то полученное уравнение
является уравнением касательной
плоскости к поверхности
в точке
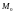 .
Можно доказать, что если на данной
поверхности провести через точку
всевозможные кривые и в этой точке
построить к ним касательные, то все эти
касательные располагаются в найденной
плоскости.
.
Можно доказать, что если на данной
поверхности провести через точку
всевозможные кривые и в этой точке
построить к ним касательные, то все эти
касательные располагаются в найденной
плоскости.
Определение. Касательной плоскостью к поверхности в ее точке (точке касания) называется плоскость, содержащая в себе все касательные к кривым, проведенным на поверхности через эту точку.
Определение. Нормалью к поверхности называется прямая перпендикулярная касательной плоскости и проходящая через точку касания.
Так как уравнение касательной плоскости имеет вид:
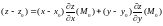 ,
,
то из условия перпендикулярности прямой и плоскости, легко получить уравнения нормали:

Если уравнение
поверхности задано неявно
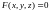 ,
,
то уравнение касательной плоскости имеет вид
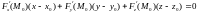 ,
,
а уравнения
нормали:
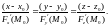
Заметим, что
полное приращение функции
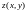 на
на
касательной
плоскости имеет вид
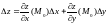 ,
то есть совпадает с полным дифференциалом
функции
.
,
то есть совпадает с полным дифференциалом
функции
.
Пример. Найти
уравнения касательной плоскости и
нормали к поверхности
 в точке
в точке
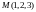 .
.
Решение.
Обозначим через
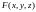 левую часть уравнения поверхности,
найдем частные производные и их значения
левую часть уравнения поверхности,
найдем частные производные и их значения
в точке :
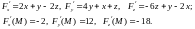
Подставляя найденные значения частных производных в уравнения касательной плоскости и нормали, получаем
 или
или
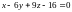 -
уравнение касательной плоскости;
-
уравнение касательной плоскости;
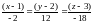 или
или
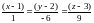 -
-
уравнение нормали.
Задачи для самостоятельного решения
1. Найти уравнения касательной плоскости и нормали к поверхности в заданной точке М0:
1.1.
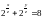 ,
,
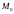 (2,2,1).
1.2.
(2,2,1).
1.2.
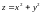 ,
(1,2,5).
,
(1,2,5).
1.3.
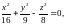 (4,3,4).
(4,3,4).
1.4.
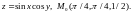
1.5.
 1.6.
1.6.

1.7.
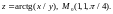
1.8.
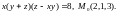
1.9.
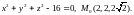
1.10.
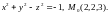
2. К поверхности
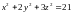 провести касательные
провести касательные
плоскости,
параллельные плоскости
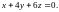
3. На поверхности
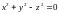 найти
точки, в которых касательные плоскости
параллельны координатным плоскостям.
найти
точки, в которых касательные плоскости
параллельны координатным плоскостям.
Ответ: 1.1.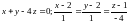 .
.
1.2.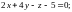
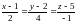 .
.
1.3.
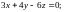
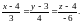
1.4.


1.5.
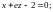

1.6.
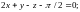
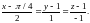
1.7.
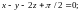
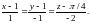
1.8.
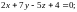

1.9.
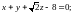
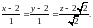
1.10.
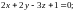
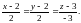
11. Производные сложных функций
Пусть
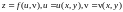 ,
тогда
,
тогда
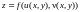 является сложной
функцией аргументов
является сложной
функцией аргументов
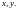 Предположим, что функции
Предположим, что функции

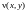 -
дифференцируемые функции своих
аргументов. Найдем
-
дифференцируемые функции своих
аргументов. Найдем
 .
.
Дадим
приращение
,
сохраняя значение
неизменным,
тогда функции
получат частные приращения
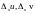 ,
и, следовательно, полное приращение
функции
,
и, следовательно, полное приращение
функции
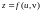 может быть записано в виде:
может быть записано в виде:
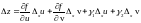 ,
,
где
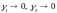 при
при
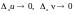 .
.
Разделив обе
части последнего равенства на
и
переходя к пределу при
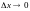 ,
получим:
,
получим:
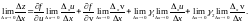 По
определению частной производной и
условию дифференцируемости функций
По
определению частной производной и
условию дифференцируемости функций
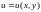 и
и
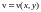 имеем
имеем
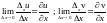 .
В силу непрерывности функций
и
по каждому аргументу
.
В силу непрерывности функций
и
по каждому аргументу
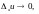
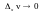 при
,
и следовательно,
при
,
и следовательно,
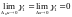 и
и
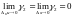 .
Тогда формула нахождения частной
производной сложной функции по
примет вид:
.
Тогда формула нахождения частной
производной сложной функции по
примет вид:
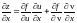 .
.
Аналогично может быть получена формула нахождения частной производной сложной функции по
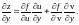
Пример. Вычислить
частные производные сложной функции
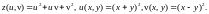
Решение.
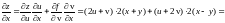
=
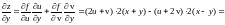
=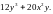
Пример.
Найти
 ,
если
,
если
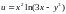 ,
,
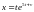 ,
,
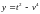 .
.
Решение. Имеем

 ,
,
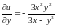 ,
,
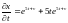 ,
,
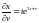 ,
,
 ,
,
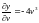 .
.
Отсюда получаем
 ,
,
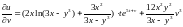 .
.
Если функция
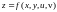 ,
где функции
,
где функции
 зависят от одного аргумента
:
зависят от одного аргумента
:
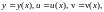 то функция
фактически зависит от одной переменной
и можно находить полную производную
то функция
фактически зависит от одной переменной
и можно находить полную производную
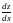 :
:
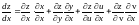 .
.
С учетом того,
что
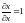 ,
а функции
зависят от одного аргумента
,
и
,
а функции
зависят от одного аргумента
,
и
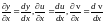 ,
получаем формулу для нахождения полной
производной:
,
получаем формулу для нахождения полной
производной:
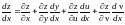 .
.
Задачи для самостоятельной работы
1. Найти
производные
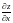 и
и
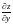 функции
функции
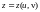 ,
где
,
где
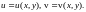
1.1.
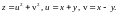
1.2.
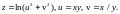
1.3.
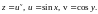
1.4.
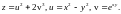
1.5.
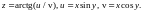
1.6.
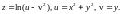
1.7.

1.8.
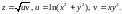
1.9.
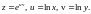
1.10.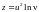 ,
,
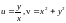 .
.
2. Найти
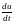 сложной функции
сложной функции
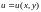 ,
где
,
где
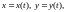 при
при
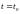 .
.
2.1.
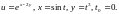
2.2.

2.3.
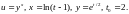
2.4.
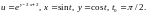
2.5.
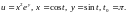
2.6.
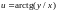 ,
где
,
где
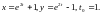
2.7.

2.8.

2.9.
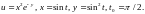
2.10.
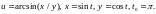
3. Найти
 ,
если
,
если
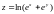 ,
где
,
где