
- •230100 «Информатика и вычислительная техника»
- •Часть 1
- •1.Основные определения
- •2. Линии и поверхности уровня
- •4. Предел и непрерывность функции
- •5. Частные производные функции нескольких
- •6. Геометрический смысл частных
- •10. Геометрический смысл полного
- •11. Производные сложных функций
- •12. Полный дифференциал сложной функции
- •13. Производная от функции, заданной неявно
- •14. Частные производные различных порядков
- •230100 «Информатика и вычислительная техника»
- •Часть 1
- •394026 Воронеж, Московский просп., 14
5. Частные производные функции нескольких
ПЕРЕМЕННЫХ
Определение.
Частной производной по
от функции
называется предел отношения частного
приращения
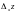 по
к приращению
при стремлении
к нулю (если он существует)
по
к приращению
при стремлении
к нулю (если он существует)
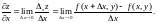
Аналогично,
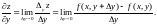
Заметим,
что
вычисляется при неизменном
,
а
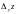
при неизменном , поэтому частной производной по от функции является производная по , вычисленная в предположении, что - постоянная.
Частной производной по от функции является производная по , вычисленная в предположении, что - постоянная.
Физический смысл частных производных следующий:
 -
скорость изменения функции в точке
-
скорость изменения функции в точке
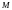 в направлении оси
,
а
в направлении оси
,
а
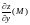 –
скорость изменения функции в точке
–
скорость изменения функции в точке
в направлении оси
 .
.
Примеры.
Найти частные производные функций:
1.
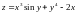 .
.
Решение. Вычислим
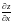 в предположении, что
имеет
в предположении, что
имеет
фиксированное
значение:
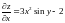 .
При вычислении
.
При вычислении
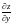 считаем, что
имеет фиксированное значение, тогда
считаем, что
имеет фиксированное значение, тогда
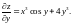
2.
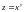 ,
,
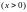 .
.
Решение. При вычислении частной производной функции
по аргументу
рассматриваем функцию
как функцию только одной переменной
,
то есть считаем, что
имеет фиксированное значение. При
фиксированном
функция
является степенной функцией аргумента
.
По формуле дифференцирования степенной
функции получаем
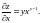 Аналогично,
при вычислении частной производной
считаем, что фиксировано значение
,
и рассматриваем функцию
как
показательную функцию аргумента
.
Получаем
Аналогично,
при вычислении частной производной
считаем, что фиксировано значение
,
и рассматриваем функцию
как
показательную функцию аргумента
.
Получаем
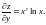
3.
Найти
 для функции
для функции
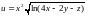 .
Найти
.
Найти
 .
.
Решение.
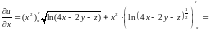
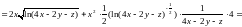
 ;
;
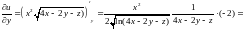
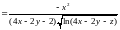
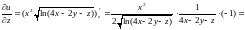

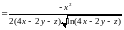 .
.
Из последнего равенства находим
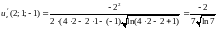 .
.
Упражнения для самостоятельной работы:
1. Найти частные производные следующих функций:
1.1. 1.2.
1.2.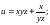 1.3.
1.3.

1.4.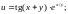 1.5.
1.5.
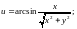 1.6.
1.6.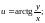
1.7.
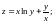 1.8.
1.8.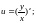 1.9.
1.9.
 1.10.
1.10.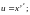
1.11.
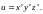
6. Геометрический смысл частных
ПРОИЗВОДНЫХ
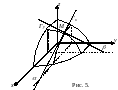 Обозначим
через
Обозначим
через
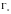 плоскую кривую, полученную при пересечении
поверхности
плоскостью
плоскую кривую, полученную при пересечении
поверхности
плоскостью
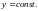 Пусть касательная к кривой
в точке
образует угол
Пусть касательная к кривой
в точке
образует угол
 с положительным направлением оси
.Тогда
с положительным направлением оси
.Тогда
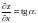 Аналогично, обозначим через
Аналогично, обозначим через
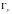 сечение поверхности
плоскостью
сечение поверхности
плоскостью
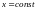 ,
,
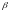 -
угол, образованный касательной к кривой
в
точке
с положительным направлением оси
.
Тогда
-
угол, образованный касательной к кривой
в
точке
с положительным направлением оси
.
Тогда
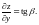 Таким образом, частная производная
в
точке
численно равна тангенсу угла наклона
касательной в точке
к кривой, полученной при пересечении
поверхности
плоскостью
Частная производная
в
точке
численно равна тангенсу угла наклона
касательной в точке
к кривой, полученной при
Таким образом, частная производная
в
точке
численно равна тангенсу угла наклона
касательной в точке
к кривой, полученной при пересечении
поверхности
плоскостью
Частная производная
в
точке
численно равна тангенсу угла наклона
касательной в точке
к кривой, полученной при
пересечении
поверхности
плоскостью

7. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ ПЕРВОГО
ПОРЯДКА В СКАЛЯРНЫХ И ВЕКТОРНЫХ ПОЛЯХ.
Частные производные находят широкое применение в физике при исследовании различных скалярных и векторных полей (температурного, гравитационного, электромагнитного, электростатического и т.д.).
1.Скалярное поле.
Пусть
-
область в трехмерном пространстве (или
на плоскости). Говорят, что в области D
задано скалярное поле, если каждой
точке
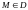 поставлено в соответствие некоторое
число
поставлено в соответствие некоторое
число
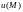 .
.
Физические примеры скалярных полей: поле температур какого-либо тела; поле зарядов на какой-либо поверхности или в сплошной среде; поле плотности масс какого-либо тела.
Физические
скалярные поля не зависят от выбора
системы координат: величина
 является функцией лишь точки
и, быть может, времени (нестационарные
поля).
является функцией лишь точки
и, быть может, времени (нестационарные
поля).
Если в
пространстве введена прямоугольная
система координат
,
то скалярное поле описывается функцией
трех переменных:
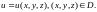
2. Векторное поле.
Говорят, что
в области
задано векторное поле, если каждой
точке
поставлен в соответствие некоторый
вектор
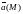 .
.
Физические
примеры векторных полей: электрическое
поле системы электрических зарядов,
характеризующееся в каждой точке
вектором напряженности
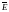 ;
магнитное поле, создаваемое электрическим
током и характеризующееся в каждой
точке вектором магнитной индукции
;
магнитное поле, создаваемое электрическим
током и характеризующееся в каждой
точке вектором магнитной индукции
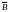 ;
поле тяготения, создаваемое системой
масс и характеризующееся в каждой точке
вектором силы тяготения
;
поле тяготения, создаваемое системой
масс и характеризующееся в каждой точке
вектором силы тяготения
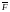 ,
действующей в этой точке на единичную
массу; поле скоростей потока
,
действующей в этой точке на единичную
массу; поле скоростей потока
жидкости,
описываемое в каждой точке вектором
скорости
 .
.
Физические
векторные поля не зависят от выбора
системы координат: в каждой точке
вектор
полностью определяется своим модулем
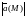 и направлением. Если в пространстве
введена прямоугольная система координат
,
то векторное поле
описывается вектор-функцией трех
переменных
и направлением. Если в пространстве
введена прямоугольная система координат
,
то векторное поле
описывается вектор-функцией трех
переменных
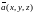 или тремя скалярными функциями - ее
координатами:
или тремя скалярными функциями - ее
координатами:
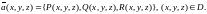
3. Производная по направлении.
Пусть
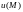 -
скалярное поле, заданное в области D;
-
скалярное поле, заданное в области D;
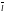 -
единичный фиксированный вектор;
-фиксированная
точка;
-
единичный фиксированный вектор;
-фиксированная
точка;
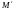 -
любая точка из
,
отличная от
и такая, что вектор
-
любая точка из
,
отличная от
и такая, что вектор
 коллинеарен
.
Пусть, далее,
коллинеарен
.
Пусть, далее,
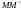 -
величина направленного отрезка
( она равна его длине
-
величина направленного отрезка
( она равна его длине
 ,
если векторы
и
,
если векторы
и
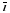 сонаправлены, и равна -
сонаправлены, и равна -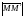 ,
если эти векторы противоположно
направлены)
,
если эти векторы противоположно
направлены)
Определение.
Число
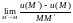 называется производной скалярного
поля
(функции
называется производной скалярного
поля
(функции
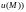 в точке
по направлению
и обозначается символом
в точке
по направлению
и обозначается символом
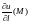 .
.
Производная по направлению является скоростью изменения функции по направлению в точке .
Если в прямоугольной системе координат
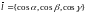 ,
то
,
то
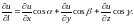
В частности,
если вектор
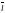 сонаправлен с одной из координатных
осей, то производная по направлению
совпадает с соответствующей частной
производной. Например,
сонаправлен с одной из координатных
осей, то производная по направлению
совпадает с соответствующей частной
производной. Например,
если
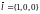 , то
, то
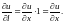
Одной из характеристик скалярного поля является градиент.
4. Градиент скалярного поля
Определение.
Градиентом скалярного поля
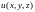 называется вектор-функция
называется вектор-функция
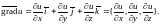
Из равенства
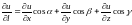 следует, что
следует, что
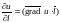 ,
откуда,
,
откуда,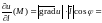
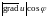 ,
так как
,
так как
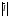 =1.
Здесь
-
угол между векторами
и
=1.
Здесь
-
угол между векторами
и
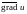 в точке
.
Очевидно, что
в точке
.
Очевидно, что
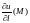 принимает
наибольшее значение при
принимает
наибольшее значение при
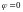 ,
то есть в направлении
в данной точке.
,
то есть в направлении
в данной точке.
Таким образом,
вектор
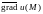 в данной точке указывает направление
наибольшего роста поля
в данной точке указывает направление
наибольшего роста поля
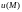 (функции
(функции
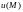 )
в этой точке, а
)
в этой точке, а
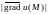 есть скорость роста функции
в этом направлении.
есть скорость роста функции
в этом направлении.
Вектор не зависит от выбора системы координат, а его модуль и направление в каждой точке определяются самой функцией .
Пример.
Найти производную функции
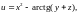 в
точке А(2,1,1) по направлению к точке
В(2,4,-3).
в
точке А(2,1,1) по направлению к точке
В(2,4,-3).
Решение.
1. Функция
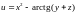 дифференцируема
в точке А(2,1,1), поэтому в этой точке
существует ее производная по любому
направлению
,
которая определяется формулой
.
дифференцируема
в точке А(2,1,1), поэтому в этой точке
существует ее производная по любому
направлению
,
которая определяется формулой
.
2.
Находим координаты вектора
.
В данном случае
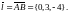
3.Находим
единичный вектор (орт)
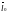 :
:
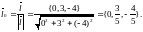
4. Вычисляем частные производные функции в точке А(2,1,1):
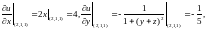
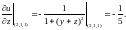
Тогда
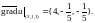
5.
Подставляя полученные значения в
формулу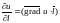 ,
получим
,
получим
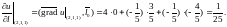
5. Потенциальное поле.
Определение.
Векторное поле
 называется
называется
потенциальным в области , если его можно представить в
этой области
как градиент некоторого скалярного
поля
:
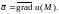
Пример.
Рассмотрим поле тяготения точечной
массы
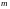 ,
помещенной в начале координат. Оно
описывается вектор-
,
помещенной в начале координат. Оно
описывается вектор-
функцией
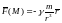 (
(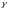 -гравитационная
постоянная,
-гравитационная
постоянная,
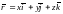 ,
,
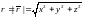 ).
С такой силой действует это поле на
единичную массу, помещенную в точку
).
С такой силой действует это поле на
единичную массу, помещенную в точку
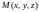 .
Поле тяготения является потенциальным,
поскольку его можно представить как
градиент скалярной функции
.
Поле тяготения является потенциальным,
поскольку его можно представить как
градиент скалярной функции
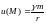 .
Действительно,
.
Действительно,
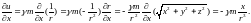 Аналогично
Аналогично
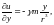
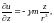 откуда
откуда
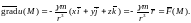
Функцию называют ньютоновским потенциалом поля тяготения точечной массы .
Поверхности уровня потенциала называются эквипотенциальными поверхностями. В рассмотренном примере эквипотенциальными поверхностями являются сферы с центром в начале координат.
Рассмотрим две характеристики векторного поля: дивергенцию и ротор.
6. Дивергенция.
Определение.
Дивергенцией
векторного поля
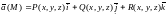 в точке
называется скалярная функция, определяемая
равенством:
в точке
называется скалярная функция, определяемая
равенством:
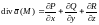
в декартовой системе координат.
Слово «дивергенция» означает «расходимость» («расхождение»). Дивергенция характеризует плотность
источников данного векторного поля в рассматриваемой точке.
Определение.
Векторное поле
называется
соленоидальным в области
,
если в этой области
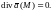
Пример.
Рассмотрим электрическое поле точечного
заряда
 ,
помещенного в начале координат:
,
помещенного в начале координат:
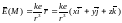 ;
;

Так как
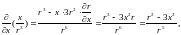
аналогично,
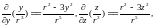 то
то
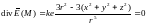 при
при
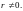 Физически этот результат означает
отсутствие источников поля в любой
точке, кроме начала координат. В начале
координат
Физически этот результат означает
отсутствие источников поля в любой
точке, кроме начала координат. В начале
координат
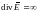 (бесконечная плотность заряда).
(бесконечная плотность заряда).
7. Ротор.
Ротором (или вихрем) векторного поля
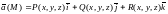
называется вектор-функция, определяемая равенством
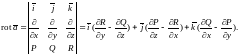
Ротор характеризует завихренность поля в данной
точке.
Равенство ротора нулю является необходимым и достаточным условием потенциальности поля.
Примеры.
1. Рассмотрим
твердое тело, вращающееся вокруг оси
 с постоянной угловой скоростью
с постоянной угловой скоростью
 .
Векторное поле скоростей
.
Векторное поле скоростей
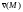 точек этого тела можно представить в
виде
точек этого тела можно представить в
виде
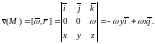
Найдем ротор
поля скоростей
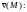
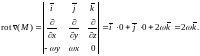
Таким образом,
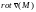 является постоянным вектором, направленным
вдоль оси вращения
,
а его модуль равен удвоенной угловой
скорости вращения тела.
является постоянным вектором, направленным
вдоль оси вращения
,
а его модуль равен удвоенной угловой
скорости вращения тела.
2. Рассмотрим
потенциальное поле
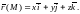 Его потенциал
Его потенциал
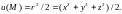 Вычислим ротор этого поля:
Вычислим ротор этого поля:
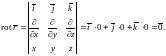
Ротор любого потенциального поля равен нулю. Поэтому говорят, что потенциальное поле является безвихревым.
Задачи для самостоятельной работы
Рассмотрим электрическое поле точечного заряда ,
помещенного в начале координат. Оно описывается в точке вектором напряженности
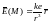 ,
где
,
.
,
где
,
.
Доказать,
что его можно представить виде
 ,
то есть, что поле потенциально.
,
то есть, что поле потенциально.
Функция
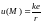 называется потенциалом электрического
поля точечного заряда
.
называется потенциалом электрического
поля точечного заряда
.
2.
Найти градиент функции
 в точке М.
в точке М.
2.1.
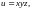
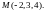
2.2.
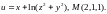
2.3.
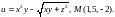
2.4.

2.5.
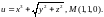
2.6.
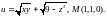
2.7.
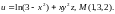
2.8.
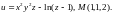
2.9.
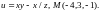
2.10.
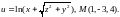
3. Найти угол
между градиентами скалярного поля
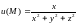 в
точках
в
точках
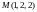 и
и
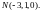
4.
Найти производную функции
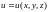 в
точке А по направлению к точке В.
в
точке А по направлению к точке В.
4.1.
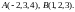
4.2.

4.3.
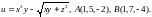
4.4.
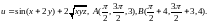
4.5.
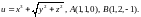
4.6.
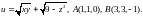
4.7.
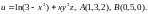
4.8.
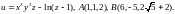
4.9.
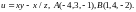
4.10.
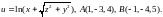
5. Найти
дивергенцию векторного поля
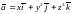
в точке
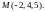
6. Проверить
соленоидальность поля
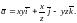
7. Показать,
что если
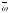 - постоянный вектор, то векторное поле
- постоянный вектор, то векторное поле
 -
соленоидально.
-
соленоидально.
8. Найти ротор
векторного поля
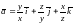 в точке
в точке
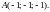
9. Показать, что поле
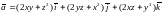
является потенциальным.
10. Найти ротор
магнитного поля

Ответы:
2.{12,-8,-6}. 3.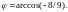 5. 84. 8.{1,1,1}. 10.
5. 84. 8.{1,1,1}. 10.
8. Оператор Гамильтона.
Введем
векторный оператор «набла» или оператор
Гамильтона:
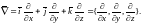
С помощью этого символического (операторного) «вектора» удобно записывать и выполнять операции векторного анализа.
В результате
умножения вектора
 на скалярную функцию
получается
:
на скалярную функцию
получается
:
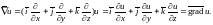
Скалярное
произведение вектора
на вектор-функцию
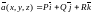 дает
дает
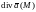 :
:
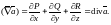
Векторное произведение вектора на вектор-функцию
дает
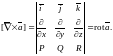
8. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
По определению полного приращения функции имеем
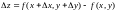 .
.
Предположим,
что
в
рассматриваемой точке
имеет непрерывные частные производные.
Выразим
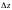 через
частные производные. Для этого представим
приращение функции в виде
через
частные производные. Для этого представим
приращение функции в виде

Применяя к первой и второй разностям теорему Лагранжа, получим
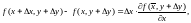 где
где
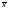 заключено между
и
заключено между
и
 ;
;
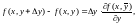 где
где
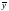 заключено между
и
заключено между
и
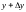 .
.
Подставляя представление разностей через производные в полное приращение функции, получим
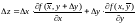 .
.
Так как по предположению частные производные непрерывны, а и заключены между и и и соответственно, то
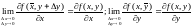 .
.
Последние равенства можно записать в виде
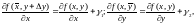 где
где
величины
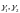 стремятся к нулю при
стремятся к нулю при
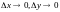 ,
то есть
,
то есть
когда
 .Тогда
полное приращение
.Тогда
полное приращение
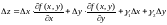 .
.
Покажем, что
сумма
 является бесконечно малой более высокого
порядка, чем
является бесконечно малой более высокого
порядка, чем
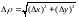 .
Действительно,
.
Действительно,
 так как
так как
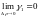 ,
а
,
а
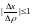 .
Сумма
.
Сумма
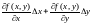 линейна относительно
и при
линейна относительно
и при
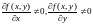 представляет собой главную часть
приращения функции.
представляет собой главную часть
приращения функции.
Определение.
Функция
,
полное приращение которой в данной
точке
может быть представлено в виде суммы
выражения, линейного относительно
и величины бесконечно малой более
высокого порядка, чем
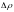 ,
называется дифференцируемой в данной
точке. Главная часть полного приращения
функции линейная относительно
называется полным дифференциалом
функции и обозначается
,
называется дифференцируемой в данной
точке. Главная часть полного приращения
функции линейная относительно
называется полным дифференциалом
функции и обозначается
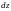 или
или
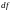 .
.
Если функция имеет непрерывные частные производные в данной точке, то она дифференцируема в этой точке и имеет полный дифференциал
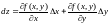 .
.
Таким образом,
полное приращение функции представимо
в виде
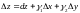 .
.
Приращения
будем называть дифференциалами
независимых переменных
 и обозначать
и обозначать
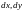 ,
тогда
,
тогда
 .
.
Аналогично,
для функции трех переменных
 полный
дифференциал равен
полный
дифференциал равен

Пример. Найти
полный дифференциал функции
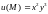 в точках
в точках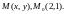
Решение.
Вычислим частные производные
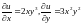 .
Запишем вид дифференциала
.
Запишем вид дифференциала
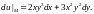 Тогда
Тогда
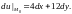
Задачи для самостоятельной работы
Найти полные дифференциалы функций:
1.
 .
2.
.
2.
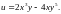
3.
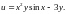 4.
4.
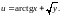
5.
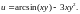 6.
6.
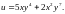
7.
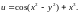 8.
8.
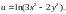
9.
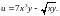
10.Найти полный дифференциал функций:
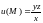 в точках
в точках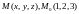 .
.
Ответ: 1.
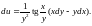
10.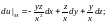
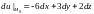 .
.
9. ПРИМЕНЕНИЕ ПОЛНОГО ДИФФЕРЕНЦИАЛА К
ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
Из формулы
следует, что
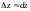 ,
тогда
,
тогда
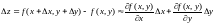 ,
следовательно,
,
следовательно,
 .
.
Пример. Вычислить
приближенно
 .
.
Решение.
Пусть
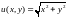 ,
,
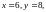
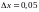 ,
,
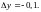 Найдем
Найдем
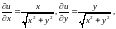
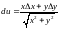 .
.
Вычислим
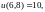
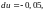
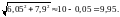
Задача для самостоятельной работы
Вычислить приближенно
1.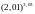 .
2.
.
2.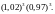 3.
3.
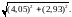
Ответ: 1. 8,29. 2. 0,97. 3. 4,998.
