
- •Часть 2
- •2. Формула тейлора для функции
- •3. Экстремумы функции двух переменных
- •4. Необходимые условия локального
- •5. Некоторые сведения о квадратичных формах
- •6. Достаточные условия локального
- •7. Условный экстремум
- •1. Дифференциалы высших порядков……............……............. 1
- •Часть 2
- •394026 Воронеж, Московский просп., 14
7. Условный экстремум
Рассмотрим функцию
(1)
при
условии, что ее аргументы являются не
независимыми переменными, а связаны
между собой
 соотношениями
соотношениями
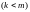 :
:
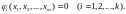 (2)
(2)
Эти соотношения называются условиями связи. Пусть
координаты
точки
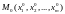 удовлетворяют уравнениям (2).
удовлетворяют уравнениям (2).
Определение.
Функция (1) имеет в точке
условный
минимум (максимум)
при условиях связи (2), если существует
такая окрестность точки
,
что для любой точки
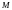 этой
окрестности (
этой
окрестности (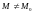 ),
координаты которой удовлетворяют
уравнениям (2), выполняется неравенство
),
координаты которой удовлетворяют
уравнениям (2), выполняется неравенство
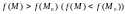 .
.
Иными словами, условный максимум (минимум)- это наибольшее (наименьшее) значение функции в точке по отношению не ко всем точкам из некоторой окрестности точки , а только к тем из них, которые связаны между собой условиями связи.
Задачу
об условном экстремуме функции можно
решать методом
исключения части переменных.
Этот метод состоит в том, что из
уравнений условий связи
переменных выражают через остальные
 переменных (если это возможно), подставляют
найденные переменные в функцию
и решают задачу об экстремуме функции
переменных.
переменных (если это возможно), подставляют
найденные переменные в функцию
и решают задачу об экстремуме функции
переменных.
Пример.
Методом исключения части переменных
найти экстремум функции
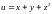 при условиях связи
при условиях связи
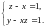
Решение.
Из условий связи находим
 .
.
Подставляя
найденные
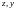 в функцию, приходим к функции одной
переменной
:
в функцию, приходим к функции одной
переменной
:
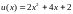 ,
для которой рассмотрим задачу о
безусловном экстремуме. Так как
,
для которой рассмотрим задачу о
безусловном экстремуме. Так как
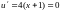 при
при
 ,
то функция
,
то функция
 имеет единственную точку возможного
экстремума. Поскольку
имеет единственную точку возможного
экстремума. Поскольку
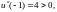 в точке
функция
имеет минимум. Из условий связи находим
соответствующие значения
:
в точке
функция
имеет минимум. Из условий связи находим
соответствующие значения
:
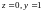 .
Итак, функция
при заданных условиях связи имеет в
точке (-1,1,0) минимум, причем
.
Итак, функция
при заданных условиях связи имеет в
точке (-1,1,0) минимум, причем
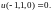
Метод Лагранжа.
Рассмотрим
задачу нахождения условного экстремума
функции
=
![]() в общем виде. Функция
=
геометрически представляет собой
некоторую поверхность, а уравнение
связи
в общем виде. Функция
=
геометрически представляет собой
некоторую поверхность, а уравнение
связи
![]()
![]() = 0 – некоторый цилиндр. Нам нужно
исследовать на экстремум линию пересечения
двух поверхностей:
= 0 – некоторый цилиндр. Нам нужно
исследовать на экстремум линию пересечения
двух поверхностей:
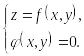
В
точке экстремума
![]() должен быть перпендикулярным цилиндру
= 0, в противном случае на линии пересечения
не будет выполняться необходимое условие
экстремума. С другой стороны
должен быть перпендикулярным цилиндру
= 0, в противном случае на линии пересечения
не будет выполняться необходимое условие
экстремума. С другой стороны
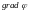 перпендикулярен поверхности уровня
перпендикулярен поверхности уровня
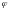
 = 0 , следовательно
= 0 , следовательно
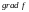 и
в точке экстремума коллинеарны, поэтому
линейно зависимые
и
в точке экстремума коллинеарны, поэтому
линейно зависимые
+
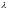 = 0, или
= 0, или
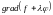 = 0.
= 0.
Записывая последнее равенство в скалярном виде и присоединяя уравнения связи, получим необходимые условия существования условного экстремума
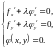 (3)
(3)
Если ввести функцию Лагранжа
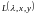 =
=
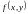 +
,
+
,
то
легко проверить, что необходимые условия
безусловного экстремума функции Лагранжа
совпадают с (3). Чтобы найти достаточные
условия экстремума, следует определить
знак полного приращения  =
–
=
–
 функции
=
в точке
функции
=
в точке
 возможного экстремума. Но при наличии
связи
= 0
=
возможного экстремума. Но при наличии
связи
= 0
=  ,
где
– полное приращение функции Лагранжа.
Поэтому достаточные условия безусловного
экстремума для функции Лагранжа будут
достаточными для условного экстремума
функции
.
,
где
– полное приращение функции Лагранжа.
Поэтому достаточные условия безусловного
экстремума для функции Лагранжа будут
достаточными для условного экстремума
функции
.
Исследуем знак второго дифференциала
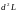 =
=
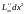 + 2
+ 2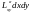 +
+
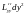 =
=
=
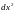
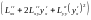 .
.
Производную
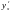 = –
= – найдем из уравнения связи
найдем из уравнения связи
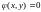 .
Учитывая это,
преобразуем следующим образом:
.
Учитывая это,
преобразуем следующим образом:
=
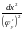
,
(4)
,
(4)
где
=
–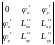 .
(5)
.
(5)
Из (4) видно, что при > 0, > 0 и функция = достигает в точке условного минимума, а при < 0 – максимума.
Задача об условном экстремуме функции (1) при условиях связи (2) эквивалентна задаче об обычном экстремуме функции Лагранжа
 ,
,
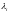 (
(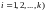 -
называются множителями
Лагранжа.
-
называются множителями
Лагранжа.
Необходимые условия условного экстремума
выражаются
системой
 уравнений:
уравнений:
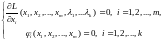 (6)
(6)
относительно
неизвестных
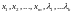 .
Если
.
Если
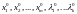 - решение системы (6), то
является точкой возможного условного
экстремума функции (1) при условиях связи
(2). Достаточные условия условного
экстремума связаны с изучением знака
второго дифференциала функции Лагранжа
- решение системы (6), то
является точкой возможного условного
экстремума функции (1) при условиях связи
(2). Достаточные условия условного
экстремума связаны с изучением знака
второго дифференциала функции Лагранжа
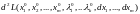 .
.
Для
каждой системы значений
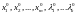 ,
полученной из (6) при условии, что
,
полученной из (6) при условии, что
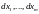 удовлетворяют уравнениям
удовлетворяют уравнениям
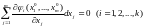 (7)
(7)
при
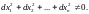
Функция имеет условный максимум
в точке
,
если для всевозможных значений
,
удовлетворяющих условиям (7) и не равных
одновременно нулю, выполняется неравенство
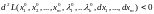 (квадратичная
форма отрицательно определена) и
условный минимум, если при этих условиях
(квадратичная
форма отрицательно определена) и
условный минимум, если при этих условиях
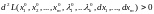 (квадратичная форма положительно
определена) , если
-
знакопеременная квадратичная форма,
то в точке
функция (1) не имеет условного экстремума.
(квадратичная форма положительно
определена) , если
-
знакопеременная квадратичная форма,
то в точке
функция (1) не имеет условного экстремума.
Пример 1. Методом Лагранжа найти экстремум функции при условиях связи
Решение. Составим функцию Лагранжа
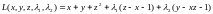
и рассмотрим систему уравнений

Она
имеет единственное решение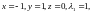
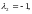 то есть
то есть
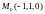 -
единственная точка возможного экстремума
функции при заданных условиях связи.
Вычислим второй дифференциал функции
Лагранжа
-
единственная точка возможного экстремума
функции при заданных условиях связи.
Вычислим второй дифференциал функции
Лагранжа
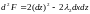 .
Подставляя в него
.
Подставляя в него
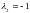 и
и
 ,
найденное из первого уравнения связи,
получаем положительно определенную
квадратичную форму от переменной
,
найденное из первого уравнения связи,
получаем положительно определенную
квадратичную форму от переменной
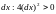 при
при
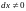 .
Отсюда следует, что функция при заданных
условиях связи имеет в точке
условный минимум.
.
Отсюда следует, что функция при заданных
условиях связи имеет в точке
условный минимум.
Пример
2. На эллипсоиде
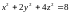 найти точку, наиболее удаленную от точки
(0,0,3).
найти точку, наиболее удаленную от точки
(0,0,3).
Решение.
Расстояние между точками
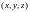 и (0,0,3)
и (0,0,3)
определяется
формулой
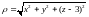 .
Поэтому
.
Поэтому
исходная
задача равносильна задаче об условном
максимуме функции
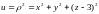 при условии связи
.
Составим функцию Лагранжа
при условии связи
.
Составим функцию Лагранжа

и рассмотрим систему уравнений:
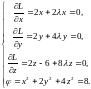
Так как
эллипсоид более всего вытянут вдоль
оси
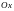 ,
то абсцисса искомой точки не может быть
равна нулю, то есть
,
то абсцисса искомой точки не может быть
равна нулю, то есть
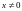 .
Поэтому из первого уравнения системы
следует, что
.
Поэтому из первого уравнения системы
следует, что
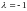 .
Тогда из второго и третьего уравнений
системы имеем
.
Тогда из второго и третьего уравнений
системы имеем
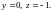 Из последнего уравнения системы находим
Из последнего уравнения системы находим
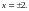 Итак, функция имеет две точки возможного
экстремума
Итак, функция имеет две точки возможного
экстремума
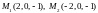 .
Из уравнения связи получим
.
Из уравнения связи получим
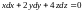 ,
откуда
,
откуда
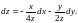 Теперь вычисляем второй дифференциал
функции Лагранжа
Теперь вычисляем второй дифференциал
функции Лагранжа
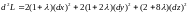 .
.
Подставим
,
координаты точки
или
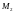 выражение для
,
получаем отрицательно определенную
квадратичную форму от двух переменных
выражение для
,
получаем отрицательно определенную
квадратичную форму от двух переменных
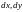 :
: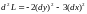 .
Отсюда следует, что функция имеет в
точках
условный максимум при заданных условиях
связи, то есть на эллипсоиде имеются
две точки
наиболее удаленные от точки (0,0,3).
.
Отсюда следует, что функция имеет в
точках
условный максимум при заданных условиях
связи, то есть на эллипсоиде имеются
две точки
наиболее удаленные от точки (0,0,3).
Пример 3. Найти условный экстремум функции
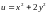

при
уравнении связи
 .
.
Решение. Составим функцию Лагранжа
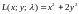
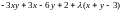 .
Обозначим
.
Обозначим
 .
.
Найдём
стационарные точки этой функции
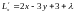 ,
,
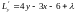 ,
,
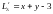 .
Решим систему уравнений
.
Решим систему уравнений

Решив
систему, находим
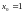 ,
,
 ,
,
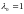 .
Имеем
.
Имеем
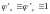 ,
,
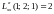 ,
,
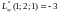 ,
,
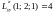 .
.
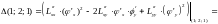
=
2 – 2(-3) + 4 = 12 > 0, следовательно,
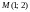 является точкой условного максимума.
является точкой условного максимума.
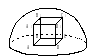
Пример 4. В полушар радиусом R вписать прямоугольный параллелепипед наибольшего объёма.
Решение. Обозначим
через x,
y,
z
измерения параллелепипеда:
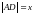 ,
,
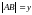 ,
,
 .
Пусть 0 – центр основания;
.
Пусть 0 – центр основания;
 .
Тогда согласно теореме Пифагора
.
Тогда согласно теореме Пифагора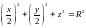 ,
,
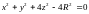 .
(8)
.
(8)
Это
есть уравнение связи. Обозначим левую
часть уравнения (8) через
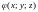 .
Фактически требуется решить следующую
задачу на условный экстремум: найти
наибольшее значение функции V
= xyz
при условии, что переменные x,
y,
z
удовлетворяют уравнению (8).
Введём в рассмотрение функцию Лагранжа
.
Фактически требуется решить следующую
задачу на условный экстремум: найти
наибольшее значение функции V
= xyz
при условии, что переменные x,
y,
z
удовлетворяют уравнению (8).
Введём в рассмотрение функцию Лагранжа
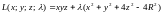 .
.
Найдём стационарные
точки функции
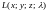 :
:
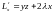 ,
,
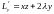 ,
,
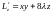 ,
,
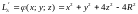 .
.
Решим систему уравнений
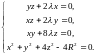
Вычитая
из первого уравнения, предварительно
умноженного на x,
второе, предварительно умноженное на
y,
получим
 .
Учитывая особенности задачи (
.
Учитывая особенности задачи (
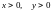 ), заключаем, что x
= y.
Действуя так же, находим, что x
= 2z.
Отсюда получаем
), заключаем, что x
= y.
Действуя так же, находим, что x
= 2z.
Отсюда получаем
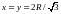 ,
,
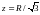 ,
,
 .
Таким образом,
.
Таким образом,
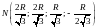 или
или
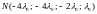 ,
если положить
,
если положить
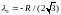 ,
является стационарной точкой функции
.
Для выяснения того, является ли
,
является стационарной точкой функции
.
Для выяснения того, является ли
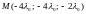 точкой экстремума, исследуем второй
дифференциал
точкой экстремума, исследуем второй
дифференциал
 при условии, что в точке М dx,
dy,
dz
связаны следующим соотношением
(являющимся следствием равенства (8)):
при условии, что в точке М dx,
dy,
dz
связаны следующим соотношением
(являющимся следствием равенства (8)):
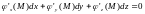 ;
;
 ;
;
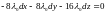 .
.
Из последнего равенства получаем
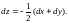 (9)
(9)
Запишем формулу второго дифференциала функции , считая её функцией трёх переменных x, y, z :
 .
.
Имеем
 ,
, 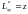 ,
, 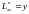 ,
,
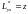 ,
, 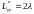 ,
,  ,
,
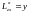 ,
,  ,
, 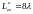 .
.



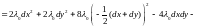
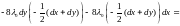
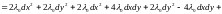
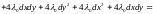
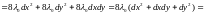
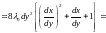
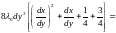
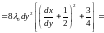
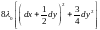 .
.
Так
как выражение в квадратных скобках
положительно при любых dx,
dy,
удовлетворяющих условию |dx|
+ |dy|
0, а
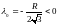 ,
то
,
то
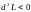 ;
следовательно, точка
;
следовательно, точка
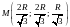 является точкой условного максимума,
и искомый параллелепипед имеет измерения
является точкой условного максимума,
и искомый параллелепипед имеет измерения
 ,
,
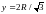 ,
,
где x,
y
– измерения основания прямоугольного
параллелепипеда, лежащего на круге
полушара, а z
– высота.
,
,
где x,
y
– измерения основания прямоугольного
параллелепипеда, лежащего на круге
полушара, а z
– высота.
Замечание.
Для
решения вопроса знакопостоянства
квадратичной формы
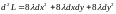 в последнем примере можно было привлечь
критерий Сильвестра. Образуем симметричную
матрицу
в последнем примере можно было привлечь
критерий Сильвестра. Образуем симметричную
матрицу
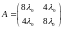 .
.
Имеем
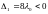 ,
,

(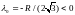 ).
Следовательно,
).
Следовательно,
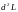 отрицательно определён и поэтому
является точкой условного максимума.
отрицательно определён и поэтому
является точкой условного максимума.
Задачи для самостоятельной работы
1. Исследуйте на условный экстремум методом исключения части переменных функцию:
1.1. при условии связи
при условии связи
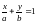 ;
;
1.2.
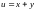 при условии связи
при условии связи
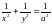 ;
;
1.3.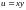 при условии связи
при условии связи
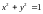 ;
;
1.4.
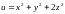 при условии связи
при условии связи
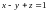 ;
;
1.5.
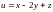 при условии связи
при условии связи
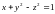 ;
;
1.6.
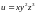 при условии связи
при условии связи

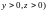 ;
;
1.7.
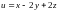 при условии связи
при условии связи
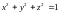 ;
;
1.8.
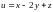 при условии связи
при условии связи
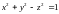 ;
;
Ответ:1.1.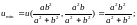
1.2.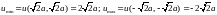 ;
;
1.3.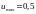 в точках
в точках
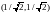 и
и
 ;
;
 в точках
в точках
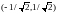 и
и
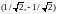 ;
;
1.4. 1.5. нет точек экстремума;
1.5. нет точек экстремума;
1.6.
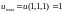 ;
1.7.
;
1.7.
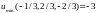 ;
;
 .1.8. нет точек
экстремума.
.1.8. нет точек
экстремума.
2. Исследуйте на условный экстремум методом Лагранжа:
2.1.
Функцию
 при условии связи
при условии связи
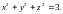
2.2. Функцию при условиях связи
 .
.
2.3.
Функцию
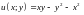 при
условии связи
при
условии связи

2.4.
Функцию
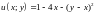 при условии связи
при условии связи
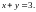
2.5.
Функцию
 при
условии связи
при
условии связи

2.6.
Функцию
 при
условии связи
при
условии связи

2.7.
Функцию
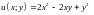 при
условии связи
при
условии связи

2.8.
Функцию
 при
условии связи
при
условии связи
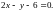
2.9.
Функцию
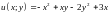 при условии связи
при условии связи
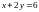 .
.
2.10.
Функцию
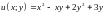 при условии связи
при условии связи
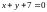 .
.
2.11.
Функцию
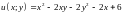 при условии связи
при условии связи
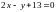 .
.
2.12.
Функцию
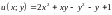 при условии связи
при условии связи
 .
.
2.13.
Функцию
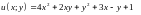 при
условии связи
при
условии связи
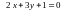 ;
;
2.14.
Функцию
 при условии связи
при условии связи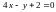 ;
;
2.15.
Функцию
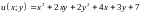 при условии связи
при условии связи
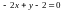 ;
;
2.16.
Функцию
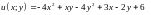 при условии связи
при условии связи
 ;
;
2.17.
Функцию
 при условии связи
при условии связи
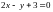 ;
;
2.18.
Функцию
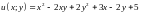 при условии связи
при условии связи
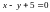 ;
;
2.19.
Функцию
 при условии связи
при условии связи
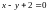 ;
;
2.20.
Функцию
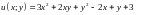 при условии связи
при условии связи
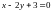 .
.
3.При
каких значениях диаметра основания
 и высоты
и высоты
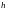
цилиндрическая
банка, объем которой равен 54 ,
имеет наименьшую поверхность?
,
имеет наименьшую поверхность?
4. При каких размерах прямоугольная банка объемом 32 см2 открытая сверху (т.е. без верхней грани), имеет наименьшую поверхность?
5. Найдите
наименьшее расстояние между точками
параболы
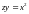 и прямой
и прямой
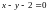 .
.
Ответ:
2.1.
 в точках (-1,1,1),(1,-1,1),(1,1,-1),
в точках (-1,1,1),(1,-1,1),(1,1,-1),
(-1,-1,-1),
 в точках (1,1,1),(-1,-1,1),(-1,1,-1),(1,-1,-1);
в точках (1,1,1),(-1,-1,1),(-1,1,-1),(1,-1,-1);
2.2.
 в точках
в точках

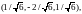
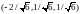 ,
,
 в точках
в точках
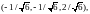

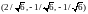 .
3.
.
3.
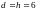 .
4.
.
4.
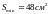 при высоте 2 см и длинах сторон основания
равных 4 см. 5.
при высоте 2 см и длинах сторон основания
равных 4 см. 5.
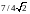 .
.
8. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ
ЗНАЧЕНИЯ ФУНКЦИИ
Если функция дифференцируема в ограниченной замкнутой области, то она достигает своего наибольшего (наименьшего) значения или в стационарной точке внутри области или в граничной точке области. Таким образом, для нахождения наибольшего (наименьшего) значения функции в замкнутой области, необходимо:
1) найти стационарные точки, расположенные в данной
области, вычислить значения функции в этих точках;
2) найти наибольшее и наименьшее значения функции
на линиях, образующих границу области;
3) из всех найденных значений выбрать наибольшее и наименьшее.
Пример 1. Найти наибольшее и наименьшее значения
функции
 в области
в области
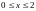 ,
,
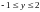 (прямоугольнике).
(прямоугольнике).
Решение. 1) Найдем стационарные точки функции из
системы
 Получаем две стационарных
Получаем две стационарных
точки
 .
Значения функции в этих точках
.
Значения функции в этих точках
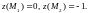
Исследуем функцию на границах области:
а)
При
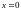 имеем
имеем
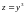 .
Эта функция монотонно
.
Эта функция монотонно
возрастает
и на концах отрезка [-1,2] принимает
значения
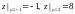 ;
;
б)
при
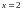 имеем
имеем
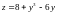 .
Найдем значения этой функции в стационарной
точке и на концах отрезка [-1,2]. Имеем
.
Найдем значения этой функции в стационарной
точке и на концах отрезка [-1,2]. Имеем
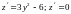 при
при
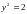 ,
или в данной области, при
,
или в данной области, при
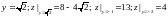 .
.
в)
При
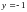 имеем
имеем
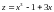 и
и
 .
Функция монотонно возрастает от
.
Функция монотонно возрастает от
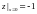 до
до
 .
.
г)
При
 имеем
имеем
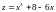 и
и
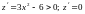
при

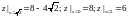 .
.
Сравнивая все найденные значения функции, заключаем, что
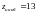 в точке (2,-1);
в точке (2,-1);
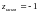 в точках (1,1) и (0,-1).
в точках (1,1) и (0,-1).
Пример 2. Найти
наибольшее и наименьшее значения функции
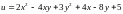 в замкнутой области (D),
заданной неравенствами
в замкнутой области (D),
заданной неравенствами
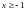 ,
,
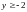 ,
,
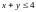 .
.
Решение.
Изобразим
область (D);
она представляет собой треугольник с
вершинами A|(-1;
-2), B(-1;
5), C(6;
-2). Найдём стационарные точки.
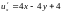 ,
,
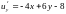 .
Решим систему уравнений
.
Решим систему уравнений
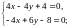


Решением этой системы является x=1, y=2. Стационарная точка M(1;2) принадлежит области (D), так как её координаты удовлетворяют всем трём неравенствам, задающим треугольник (D). Найдём значение функции в этой точке: u(M) = 2 – 8 + 12 + 4 – 16 + 5 = –1.
Исследуем
функцию на границе
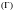 области
(D).
Граница
представляет собой объединение трёх
отрезков:
области
(D).
Граница
представляет собой объединение трёх
отрезков:
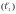 – отрезка BC,
– отрезка BC,
 – отрезка AB,
– отрезка AB,
 – отрезка AC.
– отрезка AC.
1)
 .
.
 =
2x2
– 4x(4
– x)
+ 3(4 – x)2
+
4x
– 8(4–x)
+ 5 = 2x2
– 16x
+ +4x2
+ 3(16 – 8x
+ x2)
+ 4x
– 32 + 8x
+ 5 = 9x2
– 28x
+ 21.
=
2x2
– 4x(4
– x)
+ 3(4 – x)2
+
4x
– 8(4–x)
+ 5 = 2x2
– 16x
+ +4x2
+ 3(16 – 8x
+ x2)
+ 4x
– 32 + 8x
+ 5 = 9x2
– 28x
+ 21.
Найдём
наибольшее и наименьшее значения функции
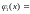 9x2
– 28x
+ 21 на отрезке [–1; 6]. Имеем
9x2
– 28x
+ 21 на отрезке [–1; 6]. Имеем
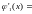 18x
– 28; x
= 14/9 – стационарная точка функции
18x
– 28; x
= 14/9 – стационарная точка функции
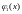 ,
14/9
[–1; 6]. Обозначим N1(14/9
; 4 –14/9 ) или N1(14/9
; 22/9 ). u(N1)
=
,
14/9
[–1; 6]. Обозначим N1(14/9
; 4 –14/9 ) или N1(14/9
; 22/9 ). u(N1)
=
=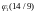 =196/9
– 392/9 + 21 = –34/9. Найдём значения
на концах отрезка [–1; 6]:
=196/9
– 392/9 + 21 = –34/9. Найдём значения
на концах отрезка [–1; 6]:
 =
u(B)
= 58;
=
u(B)
= 58;
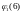 =
u(C)
= 177. Наибольшим из этих значений является
u(C)
= 177, наименьшим – u(N1)
= – 34/9.
=
u(C)
= 177. Наибольшим из этих значений является
u(C)
= 177, наименьшим – u(N1)
= – 34/9.
2)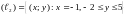 .
.
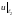 =
2 + 4y
+ 3y2
–
4 – 8y
+ 5 = 3y2
– 4y
+ 3.
=
2 + 4y
+ 3y2
–
4 – 8y
+ 5 = 3y2
– 4y
+ 3.
Найдём
наибольшее и наименьшее значения функции
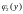 =
3y2
– 4y
+ 3 на отрезке [–2; 5];
=
3y2
– 4y
+ 3 на отрезке [–2; 5];
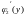 =
6y
– 4; y
= 2/3 – стационарная точка функции
,
принадлежащая отрезку [–2; 5]. Обозначим
N2(–1;
2/3). U(N2)
=
=
6y
– 4; y
= 2/3 – стационарная точка функции
,
принадлежащая отрезку [–2; 5]. Обозначим
N2(–1;
2/3). U(N2)
=
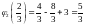 .
Найдём значения функции
на концах отрезка [– 2; 5]:
.
Найдём значения функции
на концах отрезка [– 2; 5]:
 =
u(A)
= 23;
=
u(A)
= 23;
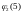 =
u(B)
= 58.
=
u(B)
= 58.
3)
 .
.
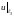 =
2x2
+ 8x
+ 12 + 4x
+ + 16 + 5 = 2x2
+ 12x
+ 33.
=
2x2
+ 8x
+ 12 + 4x
+ + 16 + 5 = 2x2
+ 12x
+ 33.
Обозначим
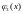 =
2x2
+ 12x
+ 33.
=
2x2
+ 12x
+ 33.
 =
4x
+ 12. Стационарная точка x
= – 3 не принадлежит отрезку [–1; 6], поэтому
она нас не интересует. Значения
на концах отрезка [–1; 6] были найдены
ранее:
=
4x
+ 12. Стационарная точка x
= – 3 не принадлежит отрезку [–1; 6], поэтому
она нас не интересует. Значения
на концах отрезка [–1; 6] были найдены
ранее:
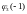 =
u(A)
= 23,
=
u(A)
= 23,
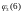 =
u(C)
= = 177.
=
u(C)
= = 177.
Сравнивая
все полученные значения, находим
 =u(C)
= u(6;
–2) = 177,
=u(C)
= u(6;
–2) = 177,
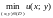 =
u(M)
= u(1;
2) = – 1.
=
u(M)
= u(1;
2) = – 1.
Задачи для самостоятельной работы
Найти наибольшее значение функции
 в
в
областях
а)
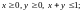 б)
б)
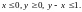
2. Найти наибольшее и наименьшее значения функции
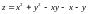 в области
в области

3. Найти наибольшее и наименьшее значения функции
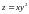 в области
в области

4.
Найдите наибольшее и наименьшее значения
функции
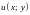 в области (D),
заданной указанными неравенствами.
в области (D),
заданной указанными неравенствами.
4.1.
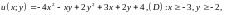
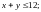
4.2.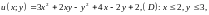
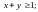
4.3.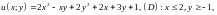
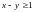 ;
;
4.4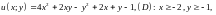
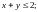
4.5.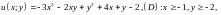
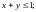
4.6.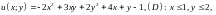
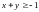 ;
;
4.7.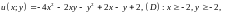
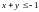 ;
;
4.8.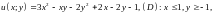
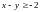 ;
;
4.9.
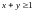 ;
;
4.10.
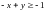 .
.
5.
Представить положительное число
 в виде произведения четырех положительных
сомножителей так, чтобы сумма их обратных
величин была наименьшей.
в виде произведения четырех положительных
сомножителей так, чтобы сумма их обратных
величин была наименьшей.
Ответ:1.
а)
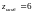 при
при
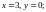 б)
б)
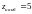 при
при
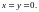 2.
при
2.
при
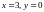 и при
и при
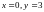 ;
при
;
при
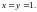 3.
3.
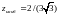 при
при
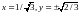 ;
;
 при
при
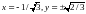 .
.
5.
9. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
В практических применениях математики часто встречается такая задача. Зависимость между переменными величинами выражается в виде таблицы, полученной опытным путем. Это могут быть результаты эксперимента, данные наблюдений или измерений, статистической обработки материала и т.п. Требуется выразить эту зависимость между переменными аналитически, то есть дать формулу, связывающую между собой соответствующие значения переменных. Такая формула облегчает анализ изучаемой зависимости. Формулы, служащие для аналитического представления опытных данных, принято называть эмпирическими формулами.
Подбор эмпирической формулы по данным наблюдений не может ставить перед собой задачу разгадать истинный характер зависимости между имеющимися переменными. Даже в том случае, когда в нашем распоряжении имеются точные значения аргумента и функции, восстановить функцию по конечному числу ее значений - задача математически неразрешимая. Тем более не следует ожидать, что это удастся сделать исходя из экспериментальных данных, которые наверняка содержат случайные ошибки измерения или статистических наблюдений.
Во многих случаях характер зависимости между переменными величинами предполагается известным из каких-либо теоретических соображений и задача подбора эмпирической формулы сводится к тому, чтобы определить числовые значения параметров, входящих в формулу данного вида.
Один
из способов подбора эмпирических формул
состоит в том, что поданным результатам
наблюдений подбирается наиболее простая
формула того или иного типа, дающая
наилучшее приближение к имеющимся
данным. При этом пользуются принципом
наименьших квадратов.
Он основан на том, что из данного
множества формул вида
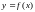 наилучшим образом изображающей данные
значения считается та, для которой сумма
квадратов отклонений наблюдаемых
значений от вычисленных является
наименьшей.
наилучшим образом изображающей данные
значения считается та, для которой сумма
квадратов отклонений наблюдаемых
значений от вычисленных является
наименьшей.
Подбор
параметров функции
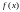 ,
основанный на этом принципе, называют
способом
наименьших квадратов.
,
основанный на этом принципе, называют
способом
наименьших квадратов.
Необходимо помнить, что способ наименьших квадратов применяется для подбора параметров после того, как вид функции определен. Если из теоретических соображений нельзя сделать никаких выводов о том, какой должна быть эмпирическая формула, то приходится руководствоваться наглядным представлениями, прежде всего графическим изображением наблюденных данных. Вид функции выбирается таким образом, чтобы график этой функции по возможности близко напоминал расположение на графике данных наблюдения.
Пусть
в результате эксперимента получены
 значений функции
значений функции
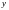 при соответствующих значениях
при соответствующих значениях
 :
:
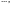
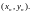 При выбранном виде функции
При выбранном виде функции
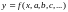 остается подобрать входящие в нее
параметры так, чтобы сумма квадратов
отклонений наблюдаемых значений от
вычисленных являлась наименьшей.
Составим функцию
остается подобрать входящие в нее
параметры так, чтобы сумма квадратов
отклонений наблюдаемых значений от
вычисленных являлась наименьшей.
Составим функцию
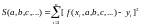 и подберем параметры
и подберем параметры
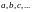 так, чтобы сумма имела наименьшее
значение. Таким образом, получилась
задача нахождения минимума функции
нескольких переменных
так, чтобы сумма имела наименьшее
значение. Таким образом, получилась
задача нахождения минимума функции
нескольких переменных
 .
Сумма принимает минимальное значение
при тех значениях параметров
,
при которых обращаются в нуль частные
производные этой функции по каждой
переменной, то есть когда
.
Сумма принимает минимальное значение
при тех значениях параметров
,
при которых обращаются в нуль частные
производные этой функции по каждой
переменной, то есть когда

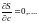
Пример.
Пусть
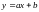 .
Найдем параметры
и
.
Найдем параметры
и
 /
Составим функцию
/
Составим функцию
 Находим частные
Находим частные
производные
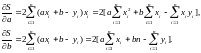
Приравнивая
каждую частную производную нулю, получаем
систему двух линейных уравнений
относительно
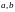
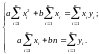
Решая
ее, находим
и
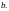
Из характера задачи следует, что система имеет определенное
решение
и что при полученных значениях
функция
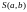 имеет минимум. Нетрудно доказать это и
на основании достаточных условий.
Действительно,
имеет минимум. Нетрудно доказать это и
на основании достаточных условий.
Действительно,
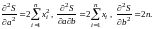
Следовательно,

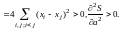
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Пискунов Н.С. Дифференциальное и интегральное исчисления/ Н.С. Пискунов.- М.: Наука, 2001. Т.1.- 250 с.
2. Мантуров О.В. Курс высшей математики/ Мантуров О.В., Матвеев Н.М.- М.: Высш. Шк.,1986.480 с.
3. Сборник задач по математике для втузов. Ч.1. Линейная
алгебра и основы математического анализа. Под ред. А.В. Ефимова, Б.П.Демидовича.М.:Наука.1993.480 с.
4. Бутузов В.Ф. Математический анализ в вопросах и задачах. Функции нескольких переменных/ Бутузов В.Ф., Крутицкая Н.Ч., Медведев Г.Н., Шишкин А.А.- М.: Высш. Шк., 1988. 288с.
5. Зимина О.В. Высшая математика/ О.В. Зимина, А.И. Кириллов, Т.А. Сальникова.- М.: Физматлит, 2005.-368 с.
6. Рябушко А.П. Индивидуальные задания по высшей математике: учеб. пособие. В 4 ч. Ч.2. Комплексные числа. Неопределенные и определенные интегралы. Функции нескольких переменных. Обыкновенные дифференциальные уравнения/ А.П. Рябушко [и др.]. Минск:Выш. шк., 2007.-396 с.
7. Лунгу К.Н. Сборник задач по высшей математике. 1 курс/Лунгу К.Н., Письменный Д.Т. Федин С.Н., Шевченко Ю.А.-М.: Рольф, 2001.-576 с.
СОДЕРЖАНИЕ
