
- •Часть 2
- •2. Формула тейлора для функции
- •3. Экстремумы функции двух переменных
- •4. Необходимые условия локального
- •5. Некоторые сведения о квадратичных формах
- •6. Достаточные условия локального
- •7. Условный экстремум
- •1. Дифференциалы высших порядков……............……............. 1
- •Часть 2
- •394026 Воронеж, Московский просп., 14
2. Формула тейлора для функции
ДВУХ ПЕРЕМЕННЫХ
Теорема.
Пусть функция
определена
и непрерывна вместе со всеми своими
частными производными до
 порядка включительно в некоторой
окрестности точки
порядка включительно в некоторой
окрестности точки
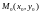 .
Тогда для любой точки
.
Тогда для любой точки
 из этой окрестности справедливо равенство
из этой окрестности справедливо равенство

где
 -
некоторая точка, лежащая на отрезке
-
некоторая точка, лежащая на отрезке
 ,
,
 .
Последнее слагаемое (остаточный член)
можно записать в форме Пеано
.
Последнее слагаемое (остаточный член)
можно записать в форме Пеано
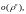 где
где
 ,
а символ
,
а символ
 означает
бесконечно малую при
означает
бесконечно малую при
 (или при
(или при
 )
функцию более высокого порядка малости,
чем
)
функцию более высокого порядка малости,
чем
 .
.
Доказательство.
Введем в рассмотрение вспомогательную
функцию
 ,
определенную на отрезке
,
определенную на отрезке
 ,
причем
,
причем
 Найдем производные функции
Найдем производные функции
 до
до
 -го
порядка включительно:
-го
порядка включительно:
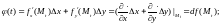

 .
.
По формуле Маклорена для функции одной переменной имеем:
 где
где

Полагая
 ,
получим
,
получим
 .
.
С учетом
того, что
 ,
,
 ,
,
 имеем
имеем

В частности,




 +
+



+ .
.
Остаточный член
 можно
можно
записать в виде , где
 .
.
Пример.
Разложить функцию
 по
формуле Тейлора с центром разложения
в точке
по
формуле Тейлора с центром разложения
в точке
 до членов второго порядка включительно.
до членов второго порядка включительно.
Решение.
Найдем частные производные функции
 до второго порядка включительно:
до второго порядка включительно:
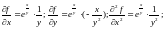


В точке имеем



 Подставляя эти
выражения в формулу Тейлора, получаем
Подставляя эти
выражения в формулу Тейлора, получаем

В форме
Пеано

Пример.
Разложить
функцию
 по формуле Тейлора в окрестности точки
M0(2;
1) до членов второго порядка включительно.
Пользуясь этой формулой, найти приближённое
значение функции в точке M(2,05;
0,38).
по формуле Тейлора в окрестности точки
M0(2;
1) до членов второго порядка включительно.
Пользуясь этой формулой, найти приближённое
значение функции в точке M(2,05;
0,38).
Решение. Найдём значение функции и частных производных функции до 2-го порядка включительно в точке M0(2; 1):
 ;
;
 ;
;
 ;
;
 ,
,
 ;
;

 ;
;
 ;
;


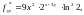

Воспользуемся формулой Тейлора:

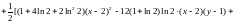
 ,
,
где
 .
.
Найдём
приближённое значение f(2,05;
0,38), отбросив в последнем равенстве
остаточный член
 :
:
f(2,05; 0,98) 2 + 2(1 + ln2)0,05 – 6 ln2(– 0,02) +
+ [(1
+ 4 ln2 + 2 ln2
20,052
– 12(1
+ln2) ln20,05(–0,02)
+
[(1
+ 4 ln2 + 2 ln2
20,052
– 12(1
+ln2) ln20,05(–0,02)
+
+ 18ln2 2(–0,02)2 = 2 + 0,1 (1 + ln2) – 0,12ln2 +
+
[(1+
4 ln2 + 2 ln22)
0,0025
– 0,012(1+
ln2)ln2+ 0,0072ln22

Задачи для самостоятельной работы
1.Разложить
данную функцию по формуле Тейлора с
центром разложения в точке

1.1.

1.2.

1.3.
 .
.
2.Разложить данную функцию по формуле Тейлора с центром
разложения в данной точке до членов указанного порядка
включительно
2.1. до членов второго порядка;
до членов второго порядка;
2.2.
 до членов третьего порядка;
до членов третьего порядка;
2.3.
 до членов третьего порядка;
до членов третьего порядка;
2.4.
 до членов четвертого порядка;
до членов четвертого порядка;
2.5.
 до членов второго порядка.
до членов второго порядка.
Ответы:
1.1.

1.2.
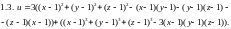
2.1.
2.2

2.3.
2.4.
+
2.5.
3. Экстремумы функции двух переменных
Определение. Точка называется точкой
локального
максимума
(минимума)
функции
,
если существует такая
 окрестность
окрестность
 точки
,
что
точки
,
что
 для любой точки
для любой точки
 .
.
Точка называется точкой локального экстремума, если она является либо точкой локального максимума, либо
точкой локального минимума.
Приведем еще одно определение максимума и минимума функции.
Пусть
 тогда
тогда
 .
.
Если
 при всех достаточно малых приращениях
при всех достаточно малых приращениях
независимых переменных, то функция достигает
максимума
в точке
 .
.
Если
 при всех достаточно малых приращениях
при всех достаточно малых приращениях
независимых переменных, то функция достигает минимума в точке .
Эти формулировки переносятся без изменения на функции любого числа переменных.
Теорема1(необходимое
условие экстремума). Если
 - точка локального экстремума функции
,
имеющей непрерывные частные производные
- точка локального экстремума функции
,
имеющей непрерывные частные производные
 в этой точке, то
в этой точке, то


Доказательство.
Дадим переменной
определенное значение
 .
Тогда функция
.
Тогда функция
 будет функцией одной переменной
.
Так как при
будет функцией одной переменной
.
Так как при
 она имеет экстремум,
она имеет экстремум,
и имеет
непрерывную производную
 ,
то
,
то

Аналогично
доказывается, что

Эта теорема не является достаточной для исследования вопроса об экстремальных значениях функции, но позволяет находить эти значения в тех случаях, в которых мы заранее уверены в существовании максимума или минимума.
Пример.
Функция
 имеет производные
имеет производные
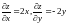 ,
которые обращаются в нуль при
,
которые обращаются в нуль при
 .
.
Но эта функция при указанных значениях не имеет ни максимума, ни минимума. Действительно, эта функция равна нулю в начале координат и принимает в как угодно близких точках от начала координат как положительные, так и отрицательные значения.
Точки,
в которых
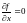 (или не существует) и
(или не существует) и
 (или не существует), называются критическими
точками функции
.
(или не существует), называются критическими
точками функции
.
Точки, в которых все частные производные первого
порядка равны нулю, называются точками стационарности функции или стационарными точками.
Для исследования функции в критических точках установим достаточные условия экстремума функции двух переменных.
Теорема 2 (достаточные условия экстремума). Пусть в некоторой области, содержащей точку , функция имеет непрерывные частные производные до третьего порядка включительно, пусть, кроме того, точка - стационарная, то есть
Обозначим

и
 .
Тогда:
.
Тогда:
если
 ,
то в точке
функция
имеет минимум;
,
то в точке
функция
имеет минимум;если
 ,
то в точке
функция
имеет максимум;
,
то в точке
функция
имеет максимум;если
 ,
то экстремума в точке
нет;
,
то экстремума в точке
нет;если
 ,
то экстремум в этой точке может быть и
,
то экстремум в этой точке может быть и
может не быть (требуется дальнейшее исследование).
Доказательство. Напишем формулу Тейлора второго порядка для функции

+

 ,
,
где
 По условию
-
точка стационарности, поэтому
По условию
-
точка стационарности, поэтому
 .
Из формулы Тейлора следует
.
Из формулы Тейлора следует


+ .
.
Используя введенные обозначения, запишем
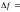

 .
.
Выражение
в квадратных скобках, то есть второй
дифференциал
 ,
является квадратичной формой относительно
,
является квадратичной формой относительно
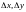 .
Если выполнено условие
.
Если выполнено условие
 ,
то квадратичная форма сохраняет
постоянный знак. Этот знак совпадает
со знаком
,
то квадратичная форма сохраняет
постоянный знак. Этот знак совпадает
со знаком
 в некоторой окрестности точки
,
поскольку
-
величина бесконечно малая более высокого
порядка малости, чем
в некоторой окрестности точки
,
поскольку
-
величина бесконечно малая более высокого
порядка малости, чем
 .
Если:
.
Если:
1) то
то
 и
при любых достаточно
и
при любых достаточно
малых
.
Следовательно, при
 в точке
в точке
функция имеет минимум;
2)
, то
то
 и
при любых достаточно малых
.
Следовательно, при
и
при любых достаточно малых
.
Следовательно, при
 в точке
функция
имеет максимум;
в точке
функция
имеет максимум;
3) если
 то
то
 может
принимать как положительные, так и
отрицательные значения, поэтому
экстремума в точке
нет;
может
принимать как положительные, так и
отрицательные значения, поэтому
экстремума в точке
нет;
4)если
,
то и при
и при
 знак приращения
функции определяется последующими
слагаемыми в формуле Тейлора, поэтому
требуется дополнительное исследование.
знак приращения
функции определяется последующими
слагаемыми в формуле Тейлора, поэтому
требуется дополнительное исследование.
Пример.
Найти локальные экстремумы функции
 в области
в области

Решение.
Найдем
 Решив
Решив
систему
уравнений получим
получим
стационарную
точку
 ,
то есть
,
то есть
 .
В этой точке выполнены необходимые
условия экстремума. Найдем вторые
частные производные
.
В этой точке выполнены необходимые
условия экстремума. Найдем вторые
частные производные

Вычислим
 .
Так как
,
то точка
является точкой локального максимума.
.
Так как
,
то точка
является точкой локального максимума.
Пример. Найти точки экстремума функции
 .
.
Решение.
Найдём
стационарные точки функции
 ,
,
 .
Решим систему уравнений
.
Решим систему уравнений


Решением системы являются точки M1(-2; -3), M2(-2; 1). Исследуем эти стационарные точки на экстремум, для чего найдём частные производные второго порядка:
 ,
,
 ,
,
 .
.
Имеем
 .
.
 ,
следовательно, M1(–2;
–3) не является точкой экстремума.
,
следовательно, M1(–2;
–3) не является точкой экстремума.
 ,
что говорит о том, что M2(–2;
1) является точкой экстремума. А так как
,
что говорит о том, что M2(–2;
1) является точкой экстремума. А так как
 ,
то заключаем, что M2
– точка минимума.
,
то заключаем, что M2
– точка минимума.
Задачи для самостоятельной работы
Найти точки локального экстремума следующих функций двух переменных:
1.
 2.
2.

3.
 4.
4.

5.
 6.
6.

7.
 8.
8.

9.
 10.
10.

11.
 .
12.
.
12.
 .
.
13.
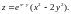 14.
14.

15.

1
17.

18.

19.
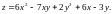
20.

Ответы:
1. 2.
точек экстремума нет.
2.
точек экстремума нет.
3.
 4.
4.
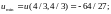
 5.
5.


6.
 7.
В точке (0,0) экстремума нет,
7.
В точке (0,0) экстремума нет,
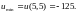 8.
8.
 9.
9.
 10.
10.
 11.
Экстремумов нет. 12.
11.
Экстремумов нет. 12.
 при
при
 и при
и при
 при
при
 экстремумов нет. 13.
экстремумов нет. 13.
 при
при
 при
экстремумов нет. 14.
при
экстремумов нет. 14.
 15.
15.

