ФГБОУ ВПО «Воронежский государственный

технический университет»

Кафедра теоретической и прикладной механики

Методические указания

для самостоятельной работы при решении задач

по дисциплине «Сопротивление материалов»

(раздел «Кручение»)

для студентов очной формы обучения

Воронеж 2012

Составители: канд. техн. наук А.А. Воропаев,

канд. техн. наук Ф.Х. Томилов

УДК 539.3/6

Методические указания для самостоятельной работы при решении задач по дисциплине «Сопротивление материалов» (раздел «Кручение») для студентов очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. А.А. Воропаев, Ф.Х. Томилов. Воронеж, 2012. 35 с.

В методических указаниях представлен набор задач, посвященных расчетам на прочность и жесткость при кручении валов. Приведены краткие сведения из теории и примеры решения типовых задач.

Предназначены для студентов очной формы обучения.

Методические указания подготовлены в электронном виде в текстовом редакторе MS Word XP и содержатся в файле «сопромат12_3.doc».

Ил. 3. Библиогр.: 1 назв.

Рецензент канд. техн. наук, доц. В.А. Рябцев

Ответственный за выпуск зав. кафедрой д-р техн. наук,

проф. Д.В. Хван

Печатается по решению редакционно-издательского совета Воронежского государственного технического университета

© ФГБОУ ВПО «Воронежский государственный

технический университет», 2012

1. Кручение

1.1. Основные понятия и зависимости

Под кручением понимают такой вид деформирования, при котором в поперечных сечениях бруса возникает только крутящий момент. Брус, работающий на кручение, называют валом. Крутящий момент в поперечном сечении вала, нагруженного скручивающими моментами, определяется по формуле

М = , (1)

где M - i-й скручивающий момент, приложенный по одну сторону от указанного сечения; n - число моментов, приложенных к отсеченной части вала. При записи этого соотношения принимается, например, следующее условное правило знаков, согласно которому крутящий момент в рассматриваемом сечении считается положительным, когда М вращает отсеченную часть вала против хода часовой стрелки, относительно оси z вала, если смотреть со стороны отброшенной части.

Условие прочности при кручении круглого вала записывается в виде

, (2)

где - допускаемое касательное напряжение для материала вала; W = - полярный момент сопротивления сечения вала с наружным диаметром D и диаметром соосного отверстия d, где [1].

Взаимный угол поворота концевых сечений вала со ступенчатым изменением жесткости определяют по формуле

, (3)

где G - модуль сдвига i -того участка; M -крутящий момент на i-том участке; l -длина i-го участка; полярный момент инерции сечения i-го участка вала; m- число участков вала.

Условие жесткости по относительному углу закручивания представляется в виде

, (4)

Условие жесткости по абсолютному углу закручивания записывается в виде

, (4а)

где -допускаемое значение абсолютного угла закручивания.

Если рассчитывается статически неопределимый вал, то раскрытие статической неопределимости проводят по следующему алгоритму:

1) составляют уравнение равновесия;

2) устанавливают степень статической неопределимости;

3) рассматривая схему деформирования вала, составляют уравнение совместности перемещений;

4) в уравнении совместности перемещений выражают углы поворота сечений через крутящие моменты и жесткости ступней вала с помощью формулы (3);

5) решая систему из уравнений равновесия и совместности перемещений, определяют реактивные моменты.

2. Примеры расчета

1. Вал трубчатого сечения с внешним диаметром и внутренним диаметром жестко защемлен с левой стороны и нагружен скручивающими моментами и (рис. 1). Определить допускаемые значения и , если , , .

1. 

Рис. 1

Решение

В данной задаче требуется провести расчет грузоподъемности вала работающего на кручение. Исходя из условия прочности (2), расчет грузоподъемности проводится по соотношению

, (5)

где – значение крутящего момента в опасном сечении вала; – допускаемое касательное напряжение для материала вала, заданное в условии задачи; – полярный момент сопротивления сечения вала. Для трубчатого сечения определяется по соотношению

, где .

По известным значениям и рассчитываем

.

Из условия (5) получим

.

Для определения положения опасного сечения и значения крутящего момента в этом сечении в функции заданных моментов и строим эпюру крутящих моментов. С этой целью разбиваем вал на два участка (рис. 2), нумеруя их, начиная от свободного конца вала, и записываем уравнения для на каждом из этих участков.

Рис. 2

I участок: ; II участок: . По этим данным строим эпюру крутящих моментов . Принимая во внимание, что сечение вала постоянно по его длине, на основе эпюры

приходим к выводу, что опасным является любое из сечений второго участка, где действует максимальный по абсолютной величине крутящий момент . Приравнивая значение в опасном сечении , рассчитанному из условия прочности, получим

.

Следовательно, допускаемые значения скручивающих моментов будут следующими:

; .

Проверим теперь, удовлетворяется ли при найденных значениях и условие жесткости вала. В задаче дано , следовательно, условие жесткости вала будет иметь вид

.

Размеры сечения и материал постоянны по длине вала, поэтому жесткость будет также постоянной. Это означает, что максимальный относительный угол закручивания соответствует , т.е.

.

Для трубчатого сечения полярный момент инерции определяется по формуле

.

Подставляя числовые данные получим:

,

т.е. условие жесткости удовлетворяется и окончательно принимаем , .

2. Ступенчатый вал, жестко защемленный по торцам, скручивается моментом (рис. 3,а). Диаметр левой части , а правая часть имеет диаметр и ослаблена продольным каналом диаметром . Проверить вал на прочность и жесткость, если , , , , , .

Решение

В задаче требуется провести проверочный расчет вала, на прочность и жесткость, т.е. проверить выполнение условий прочности и жесткости.

Оценим вначале прочность вала, т.е. проверим выполнение условия прочности

.

Допускаемое касательное напряжение задано в условии задачи, а полярные моменты сопротивления сечения левой и правой частей вала могут быть рассчитаны по известным значениям диаметров

;

.

Таким образом, для проверки выполнения условия прочности необходимо установить расчетное значение . С этой целью построим эпюру крутящих моментов .

Отбросим связи, приложенные к валу в защемлениях, и заменим их действия реактивными моментами и (см. рис. 3,б), направления которых может быть выбрано произвольно. Для определения двух реактивных моментов и можно составить лишь одно уравнение статики в виде суммы моментов всех сил относительно оси вала :

. (6)

Таким образом, приходим к выводу, что задача статически неопределима, а степень статической неопределимости . Это означает, что для решения задачи нужно составить одно уравнение совместности перемещений. Это уравнение можно получить из условия отсутствия поворота сечения относительно сечения (см. рис. 3, а), которое можно записать в виде

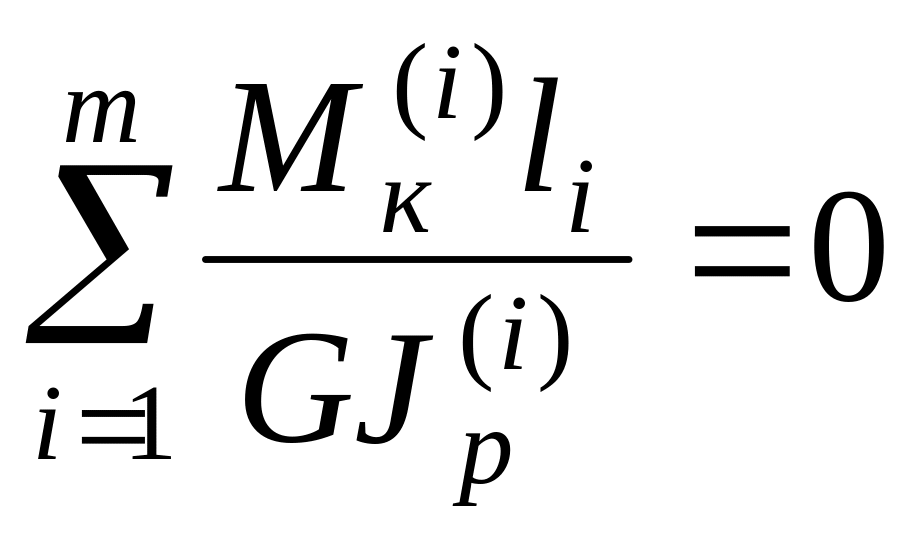, (7)

где – число участков вала.

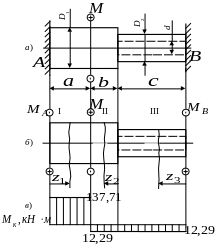
Рис. 3

Разбивая вал на 3 участка (см. рис. 3, б), запишем выражения для каждого из участков

(8)

Учитывая, что ; ; , подставим соотношения (8) в уравнение (7). При этом получим

. (9)

Решая уравнение (9) совместно с уравнением (6) с учетом того, что , получим

; .

Подставляя в эти соотношения длины участков и величины полярных моментов инерции

; ,

находим

; .

Используя соотношения (8), строим эпюру крутящих моментов (см. рис. 3,в).

Сопоставляя величины и для различных участков, приходим к выводу, что наибольшие касательные напряжения действуют в сечениях I участка, где

, а .

Подставляя эти величины в условие прочности, получим

.

Оценим перегрузку

.

Поскольку перегрузка не превышает 5 %, делаем вывод, что прочность вала обеспечена.

Проверим теперь выполнение условия жесткости, которое в данном случае будет иметь вид

.

Определим величины относительного угла закручивания для каждого из участков вала:

;

;

.

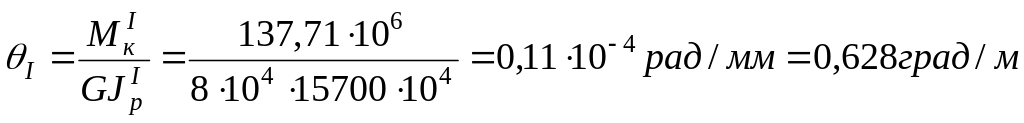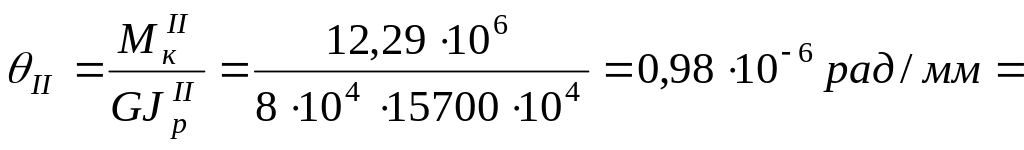
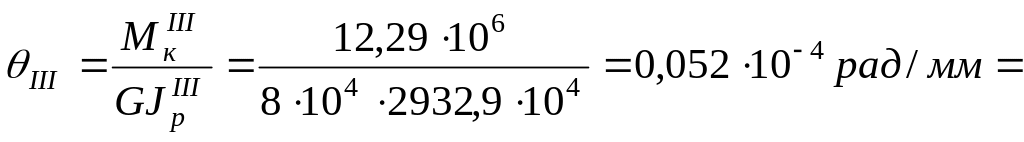
Сопоставляя полученные величины, установим, что . Следовательно, необходимая жесткость вала обеспечена.

1.3. Задачи для самостоятельного решения

1.3.1. Статически определимые валы

1. Определить диаметры ступеней вала, если МПа; а = 3м; b = 2м; М₁ = 900 Нм; М₂ = 400 Нм; М₃ = 500 Нм. Определить угол поворота сечения А по отношению к сечению В. Принять МПа.

2. Определить диаметры вала и полный угол закручивания, если m = 200 Нм; а = 0,2м; МПа; МПа.

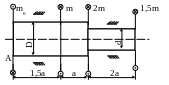
3. Определить диаметры вала d и D, если m = 0,8 кНм; МПа; ; МПа; а = 1м.

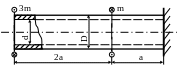
4. Определить диаметры вала и полный угол закручивания, если МПа; m = 500 Нм; а = 1 м; МПа; [φ] = 2˚.

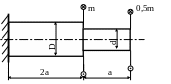
5. Определить диаметры ступеней вала и полный угол закручивания, если МПа; а = 1м; M₁ = 100Нм; М₂ = 500Нм; МПа.

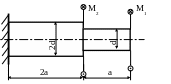
6. Определить диаметры вала из условий прочности и жесткости, если m = 1кНм; МПа; [φ] = 2˚; МПа; а = 0,2 м; .

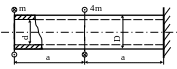
7. Определить отношение диаметров двух равнопрочных валов, передающих одинаковую мощность, если один делает , а другой .

Указание: мощность N = M·ω, где М – скручивающий момент; ω – частота вращения вала, рад/сек ( , где n – об/мин).

8. Наружный диаметр полого вала в 2 раза больше внутреннего. Определить размеры сечения вала, если он передает мощность 700 кВт при скорости вращения 100 об/мин, а наибольшие касательные напряжения в вале 60 МПа.

Замечание: скручивающий момент , где N – мощность, кВт; n – об/мин.

9. Стальной вал сплошного сечения передает мощность N = 60 кВт. Частота вращения вала n = 240 об/мин. Определить диаметр вала из расчета на прочность и жесткость, если МПа, а допускаемый угол закручивания [φ] = 1˚ (длина вала 1м, модуль сдвига МПа).

Указание: , где М – скручивающий момент, Н·м; N – мощность, кВт; n – об/мин.

10. Сплошной вал радиусом r усилен надетой на него трубой внутренним радиусом r и наружным R. Вал и труба изготовлены из одного материала и работают как одно целое. Чему должно равняться отношение R/r, чтобы описанное усиление вала позволило увеличить его грузоподъемность, т.е. скручивающий момент, вдвое.

11. Сплошной вал диаметром 40 см заменяется полым валом, у которого внутренний диаметр составляет 60 % от наружного. Определить наружный диаметр полого вала при условии, что допускаемые касательные напряжения у них одинаковы.

12. Сплошной вал круглого сечения был спроектирован в предположении определенной скорости его вращения. Затем было решено повысить скорость в 20 раз. Как изменится диаметр вала после пересчета его при неизменных остальных данных.

Замечание: выражение скручивающего момента М через мощность N и количество оборотов вала n

, где N – мощность, кВт; n – об/мин.

13. Два вала одинаковой длины из одного и того же материала воспринимают один и тот же крутящий момент. Один вал полый, с отношением диаметров . Другой вал – сплошной с диаметром D₀. Определить отношение весов полого и сплошного вала, если они равнопрочны.

14.Полый стальной вал длиной 1,8 м нагружен по концам двумя парами сил с моментами М = 0,6 кНм. Определить наружный и внутренний диаметры вала, если угол закручивания не должен превосходить 2˚, а касательные напряжения 70 Н/мм². Модуль сдвига для стали Н/мм².

15. Сплошной вал диаметром D = 12см передает постоянный вращающий момент М. Определить необходимые размеры поперечного сечения полого вала из того же материала, такой же длины, имеющего прочность, как у сплошного вала, а жесткость – в 1,5 раза большую.

1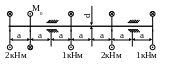 6. Подобрать диаметр поперечного сечения вала из условий прочности и жесткости, если а = 0,2м; МПа; ; МПа.

1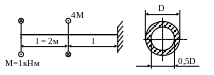 7. Определить размеры поперечного сечения вала из условий прочности и жесткости при ; [φ] = 2˚; МПа.

18. Определить размер поперечного сечения вала из условий прочности и жесткости, если а = 0,1м; b = 0,2м; ; ; МПа.

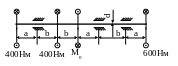
19. Вал трубчатый. Определить размеры поперечного сечения вала (d и D), если M = 0,8 кНм; ; ; МПа; а = 1м.

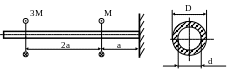
20. Определить диаметры вала и угол поворота сечения А по отношению к сечению В, если а = 1м; , m = 200 Нм; МПа.

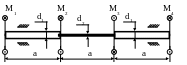
21. Проверить прочность вала. Принять: d₁ = 60мм; d₂ = 40мм; М₁ = 1,5 кНм; М₂ = 2,5 кНм; М₃ = 5 кНм; .

22. Стальной круглый вал диаметром d = 16 мм испытан на кручение. При возрастании крутящего момента на угол закручивания между двумя сечениями, отстоящими друг от друга на расстоянии ℓ = 20см увеличивается на радиана. Вычислить модуль сдвига G и коэффициент Пуассона µ, если .

23. Стержень из малоуглеродистой стали диаметром 25мм удлиняется на 0,122мм на длине 20см при растяжении силой Р = 60 кН. Этот же стержень закручивается на угол 0,75˚ на длине 20см при нагружении скручивающим моментом М = 20кНсм. Найти упругие постоянные материала Е, G, µ.

24. Полый стальной вал с наружным диаметром D = 75мм и внутренним d = 50мм имеет длину ℓ = 1м. Он закручивается на 1˚ моментами М = 3,5 кНм. Определить максимальные касательные напряжения и модуль сдвига материала.

25. Сплошной вал диаметром d = 100 мм и длиной ℓ = 6000 мм закручен на угол 4˚. Чему равно наибольшее касательное напряжение, если МПа.

26. Определить τ_мах (максимальные касательные напряжения) и проверить прочность вала, если ; m = 1кНм; D = 60мм; а = 0,2м.

27. При испытании на кручение стального образца длиной 20 см и диаметром 20 мм установлено, что при крутящем моменте М_к = 16,32кНсм угол закручивания равен 1,2˚. Предел упругости достигнут при М_к = 27кНсм. Определить модуль упругости при сдвиге и предел упругости при кручении.

28. Как изменится максимальное касательное напряжение и относительный угол закручивания, если сплошной вал заменить полым, вес которого на 20% меньше и отношение внутреннего диаметра к наружному равно 0,6.

29. Два вала, один из которых сплошной, а другой полый, имеют одинаковый вес и передают одинаковый крутящий момент. Длина валов и материал одинаковы. У какого вала наибольшие касательные напряжения будут больше и во сколько раз, если внутренний диаметр полого вала составляет 60% от наружного.

30. Наружный диаметр полого вала в два раза больше внутреннего. Этот вал на 20% легче сплошного вала, спроектированного при допускаемом напряжении на сдвиг . Чему равны наибольшие касательные напряжения в полом вале при одинаковых крутящих моментах.

31. Чтобы уменьшить вес сплошного круглого вала на 20%, заменили его полым, наружный диаметр которого в 2 раза больше внутреннего. Чему будут равны наибольшие касательные напряжения в полом вале, если в сплошном они были равны 6кН/см²?

32. Найти максимальные касательные напряжения на участках вала, проверить прочность вала, если ; m = 1кНм; d = 40мм; D = 60мм; а = 0,2м.

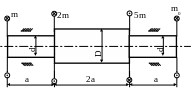
33. Проверить прочность вала. Определить угол поворота сечения А по отношению к сечению В, если m = 1кНм; а = 1м; ; d = 40мм; D = 60мм; МПа.

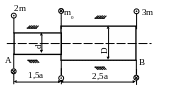
34. Для заданного вала построить эпюры крутящего момента, угла закручивания φ и найти наибольшие касательные напряжения. Проверить прочность вала, если ; М = 2кНм; d = 2см; МПа; ℓ = 1м.

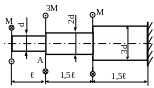
35. Проверить прочность вала. Определить угол закручивания сечения А по отношению к сечению В. Принять: а = 2м; М₁ = 2кНм; М₂ = 5кНм; М₃ = 3кНм; МПа; d₁ = 20мм; d₂ = 40мм; .

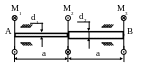
36. Вал, защемленный с одного края, нагружен моментами М. Диаметры участков d₁ = 40мм; d₂ = 60мм. На 2-м участке максимальные касательные напряжения . Определить максимальные касательные напряжения на 1-м участке.

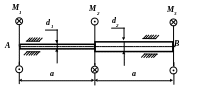
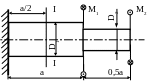
37. Определить максимальное напряжение в сечении I – I и угол поворота этого сечения, если D₁ = 100мм; D₂ = 50мм; М₁ = 500 Нм; М₂ = 1500Нм; а = 20см; Н/мм².

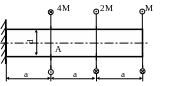
38. Найти допустимое значение момента [M]. Определить угол закручивания φ_А сечения А, если d = 5см; а = 1м; ; МПа.

3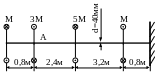 9. Определить величину М и максимальные напряжения , если МПа, а угол закручивания сечения А равен 1˚.

4

М₂

М₁

0. Определить момент М₂, если . Принять: МПа; а = 0,5м; d = 30мм; М₁ = 0,5кНм.

B

A

a

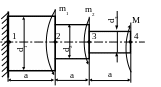
a

a

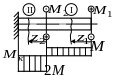
41. Стальной ступенчатый вал нагружен скручивающими моментами m₁, m₂, M. При каком значении момента М абсолютный угол закручивания в сечении «4» будет равен нулю, если а = 1м; m₁ = 20кНм; m₂ = 10кНм; d₃ = 5см; d₂ = 10см; d₁ = 20см; Н/мм².

42. Определить наибольший крутящий момент, который может быть приложен к стальному валу диаметром 10мм, если допускаемое напряжение не должно превосходить 15кН/см². Какова будет длина вала, если допускаемый угол закручивания [φ] = 2˚; кН/см².

4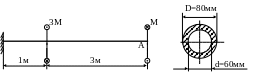 3. При заданном допускаемом напряжении [τ] = 20МПа определить величину момента М и угол закручивания φ сечения А.

44. Для определения необходимого диаметра сплошного стального вала задано допускаемое касательное напряжение [τ] = 80МПа и допускаемый угол закручивания 1˚ на длине вала, равной 1м. При каких величинах крутящего момента можно ограничиться определением диаметра только по допускаемому напряжению или только по допускаемому углу закручивания?

45. Два вала одинаковой длины и массы изготовлены из одного и того же материала. Один вал полый с отношением диаметров . Другой – сплошной диаметром D₀. Найти отношение крутящих моментов, которые могут быть приложены к валам при одинаковом допускаемом напряжении.

46. Определить величину крутящего момента М_к, при котором расчет круглого вала на прочность дает тот же диаметр, что и расчет на жесткость. Найти величину этого диаметра. Принять допускаемое касательное напряжение [τ] = 80 Н/мм², допускаемый относительный угол закручивания ˚/м, модуль сдвига Н/мм².