2.3. Классификация корректирующих кодов

Помехоустойчивые или корректирующие коды делятся на блочные и непрерывные. К блочным относятся коды, в которых каждому символу алфавита сообщений соответствует блок (кодовая комбинация) из n(i) элементов, где i - номер сообщения. Если n(i)=n, т.е. длина блока постоянна и не зависит от номера сообщения, то код называется равномерным. Такие коды чаще применяются на практике. Если длина блока зависит от номера сообщения, то блочный код называется неравномерным. В непрерывных кодах передаваемая информационная последовательность не разделяется на блоки, а проверочные элементы размещаются в определенном порядке между информационными. Проверочные элементы в отличие от информационных, относящихся к исходной последовательности, служат для обнаружения и исправления ошибок и формируются по определенным правилам.

Равномерные блочные коды делятся на разделимые и неразделимые. В разделимых кодах элементы разделяются на информационные и проверочные, занимающие определенные места в кодовой комбинации. В неразделимых кодах отсутствует деление элементов кодовых комбинаций на информационные и проверочные. Примером такого кода является семиэлементный телеграфный код №3 с весом каждой кодовой комбинации, равным трем. Этот код может служить только для обнаружения ошибок на основании изменения веса.

Разделимые коды делятся на систематические или линейные и несистематические или нелинейные. Линейные коды получили свое название потому, что их проверочные элементы представляют линейные комбинации информационных элементов. Большую и важную подгруппу линейных кодов образуют циклические коды. Линейные коды реализуются наиболее просто, что привело к их широкому использованию в УЗО. Для линейного кода применяется обозначение (n, k) - код, где n - число элементов в комбинации; k - число информационных элементов. Нелинейные коды характеризуются наличием двух или более систем проверок внутри каждой кодовой комбинации. Наиболее часто используются проверки на чётность числа единиц и нулей в разрешенных кодовых комбинациях.

2.4. Линейные коды

Пусть имеется разрешенная кодовая комбинация a₁ a₂ ... a_k b₁ b₂ ... b_r линейного (n, k) - кода, где a₁ ... a_k - множество информационных элементов; b₁ ... b_r - множество проверочных элементов. Как уже указывалось выше, в линейных кодах проверочные элементы являются линейной комбинацией информационных. Значение любого проверочного разряда

.

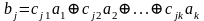Коэффициенты c_ji принимают значения 0 или 1. Таким образом линейный код полностью определяется r k коэффициентами c_ji ( j=1,2,...,r, i=1,2,...,k).

При построении линейных кодов все разрешенные кодовые комбинации могут быть найдены по нескольким исходным комбинациям, которые записываются в виде производящей матрицы G_n,k , левая часть которой представляет единичную матрицу I_k исходного простого кода, а правая B_r,k - матрицу проверочных элементов. Размерность такой матрицы n k, т.е.

G _n,k = .

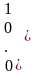Сокращенно производящую матрицу записывают в виде

G_n,k=| I_k B_r,k |.

Минимальный вес разрешенных кодовых комбинаций должен быть не меньше d₀. Так как вес каждой строки единичной матрицы W=1, вес каждой строки матрицы проверочных элементов должен быть не меньше d₀ - 1, а вес суммы по модулю два двух любых ее строк - не меньше d₀ - 2.

Пример 2.3. Построить производящую матрицу линейного кода с d₀=3 и k=4.

Пользуясь условием, что при d₀=3 , находим r=3 и n=k+r=7. Запишем все возможные строки матрицы B_r,k в порядке возрастания соответствующих двоичных чисел: 000; 001; 010; 011; 100; 101; 110; 111. Из этих восьми чисел отберем только те, которые удовлетворяют перечисленным выше условиям для матрицы B_r,k .

1. В каждой строке не менее d₀ - 1 единиц: d₀ – 1 = 2. Этому условию удовлетворяют комбинации: 011, 101, 110, 111.

2. Сумма двух любых строк по модулю два должна иметь не меньше d₀ - 2 единиц: d₀ – 2 = 1. Легко убедиться, что выбранные комбинации удовлетворяют этому требованию, например,

		0	1	1								1	0	1								0	1	1
		1	1	0								1	1	1								1	0	1
		1	0	1		,						0	1	0		,						1	1	0

Э

.

.

.

ти кодовые комбинации могут быть сопоставлены со строками единичной матрицы в любом порядке. Всего может быть построено k! (4!=1 2 3 4=24) видов производящих матриц. Располагая эти комбинации в порядке возрастания двоичных чисел, получим матрицу B_r,k :

B3,4=	0	1	1
.	1	0	1
	1	1	0
	1	1	1
	b1	b2	b3

Объединяя I₄ и B_3,4 , получим производящую матрицу линейного кода (7,4):

G7,4=	1	0	0	0	0	1	1
.	0	1	0	0	1	0	1
	0	0	1	0	1	1	0
	0	0	0	1	1	1	1
	a1	a2	a3	a4	b1	b2	b3

Общее число кодовых комбинаций N₀=2ⁿ=2⁷=128, из них разрешенных N_a=2^k=2⁴=16. Четыре из них являются строками производящей матрицы, пятая - нулевая, а остальные одиннадцать находятся суммированием по модулю два различных строк производящей матрицы G_7,4.

В свою очередь, по матрице B_r,k можно определить правила формирования проверочных элементов. Единица в первой строке каждого столбца указывает на то, что в образовании соответствующего столбцу проверочного элемента участвовал первый информационный элемент. Единица в следующей строке любого столбца говорит об участии в образовании проверочного элемента второго информационного элемента и т.д.

Найдем проверочные элементы, пользуясь матрицей проверочных элементов B_3,4. Согласно приведенным выше правилам

b₁=a₂ a₃ a₄ ,

b₂=a₁ a₃ a₄ , (2.1)

b₃=a₁ a₂ a₄ .

Процедура обнаружения ошибок основана на использовании проверок (2.1). Очевидно, что проверочные элементы, сформированные из принятых информационных, при отсутствии ошибок должны совпадать с принятыми проверочными.

Пример 2.4. Переданная кодовая комбинация имеет вид 1000011 (первая строка матрицы G_7,4). В результате действия помех на приемном конце имеем a₁’, a₂’, a₃’, a₄’, b₁’, b₂’, b₃’=1100011. Произведем проверки (2.1):

a₂’ a₃’ a₄’=1 0 0=1=b₁^* ,

a₁’ a₃’ a₄’=1 0 0=1=b₂^* ,

a₁’ a₂’ a₄’=1 1 0=0=b₃^* .

В то же время b₁’=0, b₂’=1, b₃’=1, т.е. b₁^* b₁’ , b₃^* b₃’ , что говорит о наличии ошибок в принятой кодовой комбинации. При отсутствии в принятой кодовой комбинации ошибок b₁^* b₁’=c₁=0, b₂^* b₂’=c₂=0, b₃^* b₃’=c₃=0.

Комбинация с₁ с₂ с₃ называется синдромом (проверочным вектором). Равенство нулю всех элементов синдрома указывает на отсутствие ошибок, или на то, что кодовая комбинация принята с ошибками, которые превратили ее в другую разрешенную. Последнее событие имеет существенно меньшую вероятность, чем первое.

Вид ненулевого синдрома определяется характером ошибок в кодовой комбинации. По конкретному виду синдрома можно в пределах корректирующей способности кода указать на ошибочные элементы и их исправить.

Рассмотренный код (7,4) гарантированно обнаруживает двухкратные ошибки, а исправляет только однократные. Матрица проверочных элементов B_3,4 представляет собой набор синдромов - опознавателей одиночных ошибок. Первый синдром соответствует искажению элемента a₁, второй - a₂, третий - a₃, четвертый - a₄.