Упражнения

1. Составить систему линейных алгебраических уравнений, получающуюся при аппроксимации по Галеркину решения задачи ²_/x²+²_/y²=0; x,y[–1, 1], =100 при y=1; _/n= =–1– при x=1. Ввести три невязки: в области и на двух границах, соответствующих различным краевым условиям.

2. Рассмотреть дискретизацию уравнения ²/x²=–(x) методом взвешенных невязок, если в качестве весовых функций использовать -функции Дирака: W_j=(x–x_j). Каким образом можно обеспечить выполнение краевых условий Дирихле и Неймана?

3. Провести дискретизацию уравнения

²_/x²+²_/y²+2_/y=0

проекционным методом. Функцию  на Г считать заданной.

4. Показать, что если исключить из рассмотрения невязку на Г₂, то решение, полученное с помощью метода взвешенных невязок, будет удовлетворять условию _/n=0.

5. Получить систему алгебраических уравнений для задачи (2.8), при условии, что =().

2.4 Конечные элементы и аппроксимация

Конечным элементом внутри рассматриваемой области  называют некоторую подобласть _e, геометрические размеры которой очень малы по сравнению с размерами области , но при этом остаются конечными. Элемент характеризуется числом геометрических узлов, типом аппроксимирующих функций и степенью аппроксимации неизвестной функции. Границы элементов могут быть как прямолинейными, так и криволинейными.

Решение трехмерной краевой задачи внутри элемента _e можно представить в виде суммы

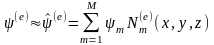. (2.25)

Базисные функции N_m^(e), относящиеся к элементу e, называются функциями формы этого элемента. Вне пределов _e они тождественно равны нулю. Семейство {N_m^(e)} должно обладать свойством полноты, т.е. при M^ ^(e)–^(e)^ 0. Каждая функция формы обычно связывается с узлом m, причем N_m^(e)(x_n, y_n, z_n)=_mn , т.е. она равна нулю во всех узлах, за исключением m-го.

На всей области определения  решение можно представить в виде

. (2.26)

Последняя запись символическая; значение функции  в точке (x, y, z) всецело определяется параметрами _m, связанными с элементом e, которому принадлежит эта точка. Если обратиться к вариационной формулировке задачи, легко показать, что полный функционал задачи, относящийся ко всей области определения, равен сумме функционалов, вычисленных на каждом элементе. Поэтому необходимое условие экстремума можно применять для каждого конечного элемента, получать систему типа (2.15), причем интегрирование в (2.16 – 2.17) производится только по _e и границе _e, если последняя является частью . Сформированные таким образом локальные системы уравнений добавляются в одну общую (глобальную) систему по определенным правилам, рассмотренным ниже.

Поскольку при реализации МКЭ требуется вычислять интегралы от функций формы и их производных по области конечного элемента _e, целесообразно ограничиться рассмотрением стандартного элемента _e*, имеющего правильную форму. Поэтому, чтобы сделать процесс вычислений единообразным для всех элементов, делается замена

.

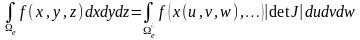Здесь det J – якобиан преобразования. Теперь функции формы {N_m^(e)} определяются раз и навсегда для стандартного элемента _e*.

Рассмотрим МКЭ-процедуру формирования матрицы системы уравнений и вектора правых частей для задачи (2.8) на примере треугольника Лагранжа (двумерный случай). Такой конечный элемент обеспечивает на границах элементов непрерывность только функции, но не ее производных.

П

Рис. 2.1.

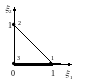усть имеется треугольный элемент с вершинами (x_i, y_i), i=1, 2, 3. Введем произвольную точку Р с координатами (x, y). Определим ее положение с помощью симплексных координат по правилу

_i = A_i/A, i = 1, 2, 3, (2.27)

где А – площадь треугольника, А_i – площадь треугольника, образованного точкой Р и двумя вершинами исходного треугольника. Очевидно, что

₁ + ₂ + ₃ = 1 и 0  _i  1 внутри треугольника

Поскольку

то

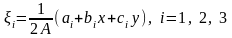. (2.28)

Формулы (28) преобразуют треугольный элемент произвольной формы, размера и ориентации в стандартный элемент (0,1), (1,0), (0,0) (рис. 2.1). Положим для простоты в (8)  = const = 1, q = 0, а для  возьмем аппроксимацию:

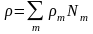(2.29)

В случае линейной аппроксимации

N_i^(e) = _i, i = 1, 2, 3, (2.30)

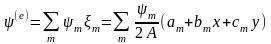. (2.31)

В результате локальная система уравнений запишется в виде:

S₁₁₁ + S₁₂₂ + S₁₃₃ = T₁₁₁ + T₁₂₂ + T₁₃₃,

S₂₁₁ + S₂₂₂ + S₂₃₃ = T₂₁₁ + T₂₂₂ + T₂₃_3, (2.32)

S₃₁₁ + S₃₂₂ + S₂₃₃ = T₃₁₁ + T₃₂₂ + T₃₃_3,

где

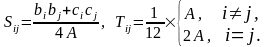
Подобным образом формируется система для каждого конечного элемента. Рассмотрим процесс объединения таких локальных систем в одну глобальную.

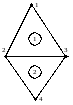
Пусть имеется два элемента с общей стороной 2–3 (рис. 2.2). Проводя дискретизацию на каждом конечном элементе, получим две системы вида (32). Переходя к глобальной нумерации узлов сетки и учитывая, что для обеспечения непрерывности функции ее значения _i в совпадающих узлах должны быть равны, т.е.

₂⁽¹⁾ = ₂⁽²⁾  ₂ и ₃⁽¹⁾ = ₃⁽²⁾  ₃ ,

левые части уравнений для первого элемента примут вид:

, (2.33а)

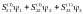, (2.33b)

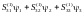, (2.33с)

Д

Рис. 2.2.

ля второго элемента

, (2.34а)

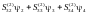, (2.34b)

. (2.34c)

Правые части уравнений получаются из левых заменой S_ijT_ij, _i_i. Складывая попарно уравнения для общих узлов ((2.33b) и (2.34a), (2.33c) и (2.34b)), получаем систему уравнений МКЭ для ансамбля из двух элементов:

,

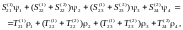_(2.35)

.

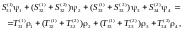
Приведенный способ объединения элементов обобщается на случай любого числа элементов. Нетрудно заметить, что полученная матрица будет симметричной, положительно определенной и сильно разреженной (т.е. содержащей много нулей вне главной диагонали). При определенной нумерации можно добиться ленточного вида матрицы, при котором все ненулевые элементы группируются возле главной диагонали. Такой способ нумерации может иметь важное значение для компактного хранения матрицы. Симметричность и положительная определенность выгодны в вычислительном плане.

Можно показать, что сформированная в виде (32) и (35) система уравнений не будет иметь решения, поскольку ее определитель равен нулю. Необходимо модифицировать систему, чтобы учесть главное краевое условие (условие Дирихле) на Г₁. Пусть в узлах 1 и 2 функция  принимает фиксированные значения ^₁ и ^₂ соответственно. Тогда первое и второе уравнения в (35), соответствующие этим узлам, заменяются уравнениями

1  ₁ = ^₁ ,

1  ₂ = ^₂ ,

а в других уравнениях члены, содержащие ₁ и ₂, переносятся в правую часть с обратным знаком. Например, для 4-го уравнения в (35) имеем

.