- •Введение
- •1. Энтропия источников сообщений
- •1.1. Дискретные ансамбли и источники
- •1.2. Количество информации в дискретном сообщении. Энтропия ансамбля
- •1.3. Условная информация. Условная энтропия. Совместная энтропия дискретного источника
- •1.4. Энтропия дискретного стационарного источника на сообщение
- •1.5. Избыточность источника дискретных сообщений
- •1.6. Эффективное кодирование. Кодирование источника равномерными кодами
- •1.7. Высоковероятные множества постоянного дискретного источника
- •1.8. Энтропия источника без памяти как скорость создания информации
- •1.9. Избыточность источника непрерывных сигналов. Количество информации в непрерывном канале
- •1.10. Скорость передачи информации и пропускная способность в непрерывном канале
- •2. Кодирование информации
- •2.1. Неравномерное кодирование с однозначным декодированием
- •2.2. Оптимальные неравномерные двоичные коды
- •2.3. Кодирование для исправления ошибок: Основные положения
- •2.4. Постановка задачи кодирования
- •2.5. Прямая теорема о кодировании в канале с шумами
- •2.6. Обратная теорема кодирования
- •2.7. Основная теорема Шеннона, ограничение возможностей использования оптимального кодирования на практике
- •3. Коды, исправляющие ошибки
- •3.1. Блоковые и сверточные коды
- •3.2. Хеммингово расстояние, Хемминговы сферы и корректирующая способность
- •3.3. Линейные блоковые коды
- •3.4. Порождающая и проверочная матрицы. Кодирование с помощью матриц g и н
- •3.5. Декодирование по стандартной таблице
- •3.6. Циклические коды
- •3.7. Кодирующие устройства циклических кодов
- •3.8. Декодирование циклических кодов по синдрому
- •3.9. Мажоритарное декодирование
- •4. Энтропия в контексте защиты информации от помех при передаче по каналу связи
- •4.1. Меры искажения. Постановка задачи защиты информации от помех при передаче по каналу связи
- •4.2. Свойства функции скорость-искажение
- •4.3. Простые примеры вычисления функции скорость-искажение
- •4.4. Функция скорость-искажение для гауссовских последовательностей
- •4.5. Эпсилон-производительность источника
- •4.6. Дифференциальная энтропия
- •4.7. Свойства дифференциальной энтропии
- •4.8. Эпсилон - энтропия источника сообщений
- •4.9. Обратная теорема кодирования для дискретного постоянного источника при заданном критерии качества
- •4.10. Прямая теорема кодирования с заданным критерием качества
- •4.11. Аксиоматическое введение в теорию энтропии вероятностных схем
- •4.12. Энтропия и условная энтропия объединенной вероятностной схемы и их свойства
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
1.7. Высоковероятные множества постоянного дискретного источника
Вероятность
любой n-последовательности
символов
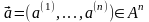 для дискретного стационарного источника
без памяти, выбирающего сообщения
из множества
А,
записывается в виде
для дискретного стационарного источника
без памяти, выбирающего сообщения
из множества
А,
записывается в виде
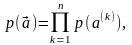 так
что количество собственной информации
в последовательности определяется
величиной
так
что количество собственной информации
в последовательности определяется
величиной
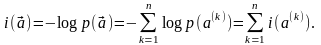 (1.12)
(1.12)
Используя для энтропии ансамбля принятое обозначение Н(А), можно сформулировать следующую теорему о высоковероятных множествах дискретного источника без памяти:
Для
любых положительных чисел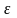 и
найдется такое N,
что для всех
и
найдется такое N,
что для всех
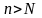 с вероятностью, большей, чем
с вероятностью, большей, чем
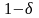 ,
выполняется неравенство
,
выполняется неравенство
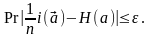 (1.13)
(1.13)
Доказательство
теоремы следует непосредственно из
выполнения закона больших чисел.
Действительно, совокупность
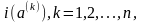 представляет
собой последовательность независимых
одинаково распределенных случайных
величин с математическим ожиданием
представляет
собой последовательность независимых
одинаково распределенных случайных
величин с математическим ожиданием
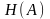 ,
принимающих ограниченные значения. К
последовательности таких случайных
величин применим закон больших чисел
в форме Чебышева (см. приложение 2):
,
принимающих ограниченные значения. К
последовательности таких случайных
величин применим закон больших чисел
в форме Чебышева (см. приложение 2):
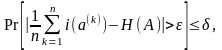 (1.14)
(1.14)
что
и доказывает утверждение, сделанное в
формулировке теоремы. Рассмотрим теперь
подмножество
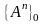 мощности
мощности
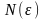 всех
n-последовательностей,
удовлетворяющих условию
всех
n-последовательностей,
удовлетворяющих условию
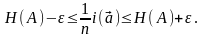 (1.15)
(1.15)
Вероятность любого элемента этого подмножества удовлетворяет неравенствам
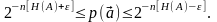 (1.16)
(1.16)
Суммируя обе части левого неравенства в (1.16) по всем элементам подмножества получим
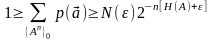 (1.17)
(1.17)
Аналогичный результат может быть получен и при анализе правой стороны неравенства (1.16).
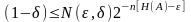 (1.18)
(1.18)
Отсюда
следует, что число элементов подмножества
с точностью определяемой значениями
и
,
оказывается приближенно равным
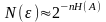 .
Таким образом, все последовательности,
выдаваемые постоянным источником, при
достаточно большой величине
могут быть разделены на две группы.
Первая группа
отличается тем, что суммарная вероятность
всех элементов этого подмножества
близка к единице, и вероятности всех
элементов его приближенно одинаковы
[см. (1.15)]. Последовательности этой группы
носят названия типичных. Вторая группа
нетипичных последовательностей является
дополнением первой до множества
.
Нетрудно убедиться, что при неравномерном
распределении на множестве А
число
типичных последовательностей для
больших n
составляет лишь очень незначительную
долю от общего числа всех последовательностей.
Действительно, при заданном числе М
элементов в множестве А
возможное
числи всех n-последовательностей
составляет
.
Таким образом, все последовательности,
выдаваемые постоянным источником, при
достаточно большой величине
могут быть разделены на две группы.
Первая группа
отличается тем, что суммарная вероятность
всех элементов этого подмножества
близка к единице, и вероятности всех
элементов его приближенно одинаковы
[см. (1.15)]. Последовательности этой группы
носят названия типичных. Вторая группа
нетипичных последовательностей является
дополнением первой до множества
.
Нетрудно убедиться, что при неравномерном
распределении на множестве А
число
типичных последовательностей для
больших n
составляет лишь очень незначительную
долю от общего числа всех последовательностей.
Действительно, при заданном числе М
элементов в множестве А
возможное
числи всех n-последовательностей
составляет
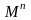 .
Тогда в отношении числа типичных
последовательностей ко всем возможным
при большом значении n
будет
определяться очень малой величиной
.
Тогда в отношении числа типичных
последовательностей ко всем возможным
при большом значении n
будет
определяться очень малой величиной
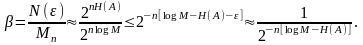 (1.19)
(1.19)
Приведем
пример. Пусть двоичный источник без
памяти выбирает сообщения из множества
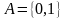 ,
причем 1 появляется с вероятностью
,
причем 1 появляется с вероятностью
 .
Для такого источника энтропия
.
Для такого источника энтропия
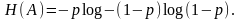 С другой стороны, обозначая черезtдолю
единиц в некоторой n-последовательности
С другой стороны, обозначая черезtдолю
единиц в некоторой n-последовательности
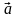 ,
для вероятности ее появления имеем:
,
для вероятности ее появления имеем:
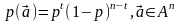 ,
так что среднее значение собственной
информации на символ в сообщении может
быть записано в виде
,
так что среднее значение собственной
информации на символ в сообщении может
быть записано в виде
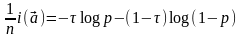 ,
где введено обозначение
,
где введено обозначение
 .
.
Таким образом, типичное множество для рассматриваемого источника состоит из последовательностей, удовлетворяющих неравенству
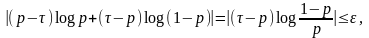
или
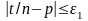 ,
,
где
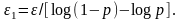 Отсюда
следует, что в типичных последовательностях
число единиц близко к np.
Отсюда
следует, что в типичных последовательностях
число единиц близко к np.
Например,
если р
= 0,2,
то
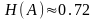 .
Типичное множество состоит из
последовательностей, число единиц в
котором близко к 0,2n.
Доля типичных последовательностей
относительно всего множества
n-последовательностей
2n
близка к
.
Типичное множество состоит из
последовательностей, число единиц в
котором близко к 0,2n.
Доля типичных последовательностей
относительно всего множества
n-последовательностей
2n
близка к
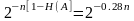 .
Так, приn
= 200 это число равно примерно 10-16,7.
.
Так, приn
= 200 это число равно примерно 10-16,7.
В
заключение отметим, что утверждение о
возможности деления множества
n-последовательностей,
создаваемых стационарными источниками
без памяти, на типичные и нетипичные
является справедливым и для пар
последовательностей {AB},{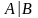 },{
},{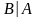 },
так что
},
так что