
- •Введение
- •1. Энтропия источников сообщений
- •1.1. Дискретные ансамбли и источники
- •1.2. Количество информации в дискретном сообщении. Энтропия ансамбля
- •1.3. Условная информация. Условная энтропия. Совместная энтропия дискретного источника
- •1.4. Энтропия дискретного стационарного источника на сообщение
- •1.5. Избыточность источника дискретных сообщений
- •1.6. Эффективное кодирование. Кодирование источника равномерными кодами
- •1.7. Высоковероятные множества постоянного дискретного источника
- •1.8. Энтропия источника без памяти как скорость создания информации
- •1.9. Избыточность источника непрерывных сигналов. Количество информации в непрерывном канале
- •1.10. Скорость передачи информации и пропускная способность в непрерывном канале
- •2. Кодирование информации
- •2.1. Неравномерное кодирование с однозначным декодированием
- •2.2. Оптимальные неравномерные двоичные коды
- •2.3. Кодирование для исправления ошибок: Основные положения
- •2.4. Постановка задачи кодирования
- •2.5. Прямая теорема о кодировании в канале с шумами
- •2.6. Обратная теорема кодирования
- •2.7. Основная теорема Шеннона, ограничение возможностей использования оптимального кодирования на практике
- •3. Коды, исправляющие ошибки
- •3.1. Блоковые и сверточные коды
- •3.2. Хеммингово расстояние, Хемминговы сферы и корректирующая способность
- •3.3. Линейные блоковые коды
- •3.4. Порождающая и проверочная матрицы. Кодирование с помощью матриц g и н
- •3.5. Декодирование по стандартной таблице
- •3.6. Циклические коды
- •3.7. Кодирующие устройства циклических кодов
- •3.8. Декодирование циклических кодов по синдрому
- •3.9. Мажоритарное декодирование
- •4. Энтропия в контексте защиты информации от помех при передаче по каналу связи
- •4.1. Меры искажения. Постановка задачи защиты информации от помех при передаче по каналу связи
- •4.2. Свойства функции скорость-искажение
- •4.3. Простые примеры вычисления функции скорость-искажение
- •4.4. Функция скорость-искажение для гауссовских последовательностей
- •4.5. Эпсилон-производительность источника
- •4.6. Дифференциальная энтропия
- •4.7. Свойства дифференциальной энтропии
- •4.8. Эпсилон - энтропия источника сообщений
- •4.9. Обратная теорема кодирования для дискретного постоянного источника при заданном критерии качества
- •4.10. Прямая теорема кодирования с заданным критерием качества
- •4.11. Аксиоматическое введение в теорию энтропии вероятностных схем
- •4.12. Энтропия и условная энтропия объединенной вероятностной схемы и их свойства
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
1.4. Энтропия дискретного стационарного источника на сообщение
Обозначим
через
 стационарный источник, выбирающий
сообщения из множества А.
Для любой n-последовательности
стационарный источник, выбирающий
сообщения из множества А.
Для любой n-последовательности
 распределение вероятностей может быть
записано следующим образом:
распределение вероятностей может быть
записано следующим образом:
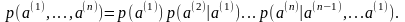
Тогда количество собственной информации в последовательности
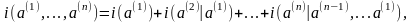
и для энтропии последовательности сообщений на выходе стационарного источника в результате статистического усреднения получим
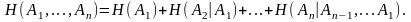 (1.9)
(1.9)
(подстрочный индекс означает номер символа в n-последовательности).
На основании (II.9) может быть введено понятие энтропии стационарного источника на сообщение. Оно получается в результате анализа последовательности
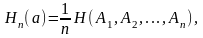
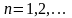 (1.10)
(1.10)
и
определяется как предел (11.10) при
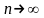 .
Доказано, что этот предел, имеющий смысл
среднего количества информации,
порождаемого источником в единицу
времени, существует.
.
Доказано, что этот предел, имеющий смысл
среднего количества информации,
порождаемого источником в единицу
времени, существует.
1.5. Избыточность источника дискретных сообщений
Исследуя свойства энтропии ансамбля дискретных сообщений с фиксированным числом К возможных состояний (мощность алфавита ансамбля — К), мы пришли к выводу, что максимальную энтропию имеет ансамбль, все сообщения которого являются равновероятными и статистически независимыми. Отсюда следует, что от источника, последовательно выбирающего сообщения из такого ансамбля, за определенный промежуток времени может быть получено максимальное количество информации.
Рассмотрим,
в какой мере реальные физические
источники удовлетворяют указанным
свойствам. Хорошим примером может
служить источник, на выходе которого
появляется последовательность букв из
алфавита мощностью
К
= 32 (русский язык). При равновероятной и
независимой передаче букв энтропия
этого источника составляет
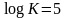 бит/символ. В действительности в
осмысленном тексте буквы передаются
не хаотически и оказываются существенно
связанными. Они, как известно, имеют
различную вероятность, и вместе с тем
появление последующих букв зависит
от предыдущего текста. Результаты
статистического анализа совокупности
текстов русской художественной прозы
позволяют сделать вывод, что энтропия
такого источника принимает значения,
не превосходящие 1,5 бит/символ. Еще более
связанным (а потому и более легко
запоминающимся) является стихотворный
текст, где энтропия принимает еще меньшие
значения.
бит/символ. В действительности в
осмысленном тексте буквы передаются
не хаотически и оказываются существенно
связанными. Они, как известно, имеют
различную вероятность, и вместе с тем
появление последующих букв зависит
от предыдущего текста. Результаты
статистического анализа совокупности
текстов русской художественной прозы
позволяют сделать вывод, что энтропия
такого источника принимает значения,
не превосходящие 1,5 бит/символ. Еще более
связанным (а потому и более легко
запоминающимся) является стихотворный
текст, где энтропия принимает еще меньшие
значения.
Ниже представлены результаты кропотливого статистического анализа энтропии письменной речи, проделанного в двух странах.
1.
В предположении, что русский алфавит
содержит 32 буквы, максимальное значение
энтропии определяется величиной бит. Учет неравновероятности букв
приводит к значению энтропии
бит. Учет неравновероятности букв
приводит к значению энтропии
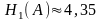 бит.
бит.
2. Подсчет числа повторений различных двухбуквенных и трехбуквенных комбинаций в отрывке из романа Л.Н. Толстого, содержащего 30000 букв дал следующие значения энтропии художественного текста, учитывающие его избыточность, связанную с наличием статистической зависимости:
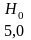
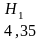
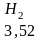
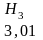
3. Шенноном даны соответствующие значения энтропии для английского языка, учитывающие более, чем двух и трехбуквенные комбинации:
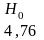
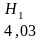



Для более полной характеристики источника дискретных сообщений вводят понятие избыточности источника с мощностью алфавита К, под которой понимают величину
 (1.11)
(1.11)
При
 источник называют источником без
избыточности.
источник называют источником без
избыточности.
Приведенные выше результаты анализа показывают, что в английском языке избыточность явно превосходит 60 %. Как показали опыты в МГУ, избыточность литературного языка русской классической прозы близка к 80 %.
Будем рассматривать последовательности символов, выбираемых из одного и того же ансамбля дискретных сообщений А, имеющие произвольную длительность , для которых ранее было введено обозначение Ап. Для реальных источников, представляющих практический интерес, связи или зависимости между элементами последовательностей, разнесенными на дискретный интервал , при неограниченном возрастании полностью исчезают. Выше было упомянуто, что существует предел при , представляющий собой среднее количество информации Н, порождаемое источником в единицу времени, и называемое энтропией стационарного источника на сообщение. С этой величиной H связана постановка задачи эффективного кодирования источника.
