
- •Введение
- •1. Энтропия источников сообщений
- •1.1. Дискретные ансамбли и источники
- •1.2. Количество информации в дискретном сообщении. Энтропия ансамбля
- •1.3. Условная информация. Условная энтропия. Совместная энтропия дискретного источника
- •1.4. Энтропия дискретного стационарного источника на сообщение
- •1.5. Избыточность источника дискретных сообщений
- •1.6. Эффективное кодирование. Кодирование источника равномерными кодами
- •1.7. Высоковероятные множества постоянного дискретного источника
- •1.8. Энтропия источника без памяти как скорость создания информации
- •1.9. Избыточность источника непрерывных сигналов. Количество информации в непрерывном канале
- •1.10. Скорость передачи информации и пропускная способность в непрерывном канале
- •2. Кодирование информации
- •2.1. Неравномерное кодирование с однозначным декодированием
- •2.2. Оптимальные неравномерные двоичные коды
- •2.3. Кодирование для исправления ошибок: Основные положения
- •2.4. Постановка задачи кодирования
- •2.5. Прямая теорема о кодировании в канале с шумами
- •2.6. Обратная теорема кодирования
- •2.7. Основная теорема Шеннона, ограничение возможностей использования оптимального кодирования на практике
- •3. Коды, исправляющие ошибки
- •3.1. Блоковые и сверточные коды
- •3.2. Хеммингово расстояние, Хемминговы сферы и корректирующая способность
- •3.3. Линейные блоковые коды
- •3.4. Порождающая и проверочная матрицы. Кодирование с помощью матриц g и н
- •3.5. Декодирование по стандартной таблице
- •3.6. Циклические коды
- •3.7. Кодирующие устройства циклических кодов
- •3.8. Декодирование циклических кодов по синдрому
- •3.9. Мажоритарное декодирование
- •4. Энтропия в контексте защиты информации от помех при передаче по каналу связи
- •4.1. Меры искажения. Постановка задачи защиты информации от помех при передаче по каналу связи
- •4.2. Свойства функции скорость-искажение
- •4.3. Простые примеры вычисления функции скорость-искажение
- •4.4. Функция скорость-искажение для гауссовских последовательностей
- •4.5. Эпсилон-производительность источника
- •4.6. Дифференциальная энтропия
- •4.7. Свойства дифференциальной энтропии
- •4.8. Эпсилон - энтропия источника сообщений
- •4.9. Обратная теорема кодирования для дискретного постоянного источника при заданном критерии качества
- •4.10. Прямая теорема кодирования с заданным критерием качества
- •4.11. Аксиоматическое введение в теорию энтропии вероятностных схем
- •4.12. Энтропия и условная энтропия объединенной вероятностной схемы и их свойства
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
1.3. Условная информация. Условная энтропия. Совместная энтропия дискретного источника
Рассмотрим
теперь
—
два совместно заданных ансамбля
и
 На
каждом из множеств
А
и
В
могут быть определены условные
распределения. Зафиксируем некоторое
сообщение
На
каждом из множеств
А
и
В
могут быть определены условные
распределения. Зафиксируем некоторое
сообщение
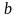 и
рассмотрим условное распределение на
множестве А.
Условное распределение на
А
относительно фиксированного значения
удовлетворяет всем свойствам безусловных
распределений и, следовательно, при
задании АВ
задаются также условные ансамбли
и
рассмотрим условное распределение на
множестве А.
Условное распределение на
А
относительно фиксированного значения
удовлетворяет всем свойствам безусловных
распределений и, следовательно, при
задании АВ
задаются также условные ансамбли
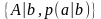 и
и ;
предполагается, что
и
;
предполагается, что
и
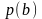 не равны 0. Для каждого сообщения
а
в ансамбле
определена
собственная информация
не равны 0. Для каждого сообщения
а
в ансамбле
определена
собственная информация
 (1.6)
(1.6)
называемая условной собственной информацией сообщения а при фиксированном сообщении . Математическое ожидание условной информации
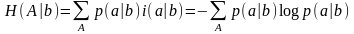
называется условной энтропией ансамбля А относительно сообщенияb.
Математическое
ожидание
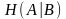 случайной величины
случайной величины
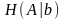 ,
определенной на ансамбле
,
определенной на ансамбле
 называется
условной энтропией ансамбля
А
относительно ансамбля
В:
называется
условной энтропией ансамбля
А
относительно ансамбля
В:
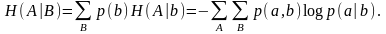 (1.7)
(1.7)
Таким же образом убеждаемся в справедливости равенства
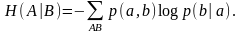 (1.7a)
(1.7a)
Математическое
ожидание собственной информации пары
сообщений
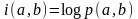 представляет собой энтропию (совместную
энтропию) ансамбля АВ:
представляет собой энтропию (совместную
энтропию) ансамбля АВ:
 (1.8)
(1.8)
Продолжим рассмотрение свойств энтропии, условной и совместной энтропии.
1.
Из определения условной вероятности
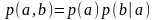 следует,
что
следует,
что
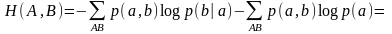

и
аналогично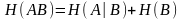 .
Эти свойства также называются
свойствами аддитивности энтропии.
.
Эти свойства также называются
свойствами аддитивности энтропии.
2.
Условная энтропия не превосходит
безусловной энтропии того же ансамбля:
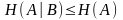 ,
причем равенство имеет место в том и
только в том случае, когда ансамбли A
и
В
статистически независимы. Доказательство
проводится аналогично доказательству
справедливости неравенства (1.3) с
использованием неравенства (1.4) для
логарифма:
,
причем равенство имеет место в том и
только в том случае, когда ансамбли A
и
В
статистически независимы. Доказательство
проводится аналогично доказательству
справедливости неравенства (1.3) с
использованием неравенства (1.4) для
логарифма:

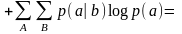

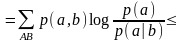
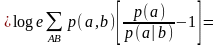
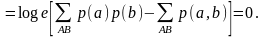
Равенство
выполняется в том и только в том случае,
когда
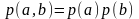 для всех
для всех
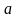 и
,
т.е. когда ансамбли A
и В
статистически
независимы
и
,
т.е. когда ансамбли A
и В
статистически
независимы
Рассмотрим
частный случай, когда
В = А,
так что Тогда
на основании свойств 1 и 2 можно сделать
вывод, что совместная энтропия
Тогда
на основании свойств 1 и 2 можно сделать
вывод, что совместная энтропия
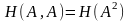 имеет наибольшее значение, равное
имеет наибольшее значение, равное
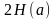 ,
когда сообщения в ансамбле A
не имеют статистической связи.
,
когда сообщения в ансамбле A
не имеют статистической связи.
3.
Из свойства 2 условной энтропии вытекает
следующая закономерность. Зададим
на ансамбле
отображение
 множества А
в множество X,
определяющее ансамбль
множества А
в множество X,
определяющее ансамбль
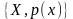 следующим образом:
следующим образом:
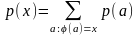 .
Тогда
.
Тогда
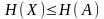 ;
знак равенства имеет место только в том
случае, когда отображение
обратимо,
т.е. когда каждому элементу х
соответствует единственный элемент а.
Для доказательства можно воспользоваться
равенством
;
знак равенства имеет место только в том
случае, когда отображение
обратимо,
т.е. когда каждому элементу х
соответствует единственный элемент а.
Для доказательства можно воспользоваться
равенством
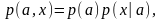 где
где ,
когда
,
когда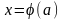 ,
и
,
и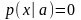 для остальных х,
т.е. когда каждое сообщение ансамбля
А
однозначно определяет сообщение ансамбля
X.
Тогда
для остальных х,
т.е. когда каждое сообщение ансамбля
А
однозначно определяет сообщение ансамбля
X.
Тогда
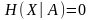 ,
и из аддитивности и неотрицательности
энтропии получим, что
,
и из аддитивности и неотрицательности
энтропии получим, что
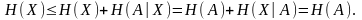
Отсюда
следует вывод, что при произвольных
отображениях
энтропия
не возрастает. Энтропия не изменяется
только тогда, когда
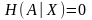 ,
т.е. когда ансамбль X
взаимно однозначно отображает
ансамбль А.
,
т.е. когда ансамбль X
взаимно однозначно отображает
ансамбль А.
4.
Для трех совместно заданных ансамблей справедливо неравенство
справедливо неравенство
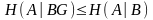 ,
которое
доказывается аналогично проведенному
при рассмотрении свойства 2. Равенство
здесь имеет место при статистической
независимости ансамблей А
и G.
Это неравенство легко обобщается на
случай
совместно заданных ансамблей. При
этом оказывается справедливым утверждение,
что
,
которое
доказывается аналогично проведенному
при рассмотрении свойства 2. Равенство
здесь имеет место при статистической
независимости ансамблей А
и G.
Это неравенство легко обобщается на
случай
совместно заданных ансамблей. При
этом оказывается справедливым утверждение,
что
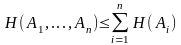 .
Знак равенства имеет место в случае
.
Знак равенства имеет место в случае
статистической
независимости сообщений в ансамблях
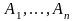 .
.
