
- •Введение
- •1. Энтропия источников сообщений
- •1.1. Дискретные ансамбли и источники
- •1.2. Количество информации в дискретном сообщении. Энтропия ансамбля
- •1.3. Условная информация. Условная энтропия. Совместная энтропия дискретного источника
- •1.4. Энтропия дискретного стационарного источника на сообщение
- •1.5. Избыточность источника дискретных сообщений
- •1.6. Эффективное кодирование. Кодирование источника равномерными кодами
- •1.7. Высоковероятные множества постоянного дискретного источника
- •1.8. Энтропия источника без памяти как скорость создания информации
- •1.9. Избыточность источника непрерывных сигналов. Количество информации в непрерывном канале
- •1.10. Скорость передачи информации и пропускная способность в непрерывном канале
- •2. Кодирование информации
- •2.1. Неравномерное кодирование с однозначным декодированием
- •2.2. Оптимальные неравномерные двоичные коды
- •2.3. Кодирование для исправления ошибок: Основные положения
- •2.4. Постановка задачи кодирования
- •2.5. Прямая теорема о кодировании в канале с шумами
- •2.6. Обратная теорема кодирования
- •2.7. Основная теорема Шеннона, ограничение возможностей использования оптимального кодирования на практике
- •3. Коды, исправляющие ошибки
- •3.1. Блоковые и сверточные коды
- •3.2. Хеммингово расстояние, Хемминговы сферы и корректирующая способность
- •3.3. Линейные блоковые коды
- •3.4. Порождающая и проверочная матрицы. Кодирование с помощью матриц g и н
- •3.5. Декодирование по стандартной таблице
- •3.6. Циклические коды
- •3.7. Кодирующие устройства циклических кодов
- •3.8. Декодирование циклических кодов по синдрому
- •3.9. Мажоритарное декодирование
- •4. Энтропия в контексте защиты информации от помех при передаче по каналу связи
- •4.1. Меры искажения. Постановка задачи защиты информации от помех при передаче по каналу связи
- •4.2. Свойства функции скорость-искажение
- •4.3. Простые примеры вычисления функции скорость-искажение
- •4.4. Функция скорость-искажение для гауссовских последовательностей
- •4.5. Эпсилон-производительность источника
- •4.6. Дифференциальная энтропия
- •4.7. Свойства дифференциальной энтропии
- •4.8. Эпсилон - энтропия источника сообщений
- •4.9. Обратная теорема кодирования для дискретного постоянного источника при заданном критерии качества
- •4.10. Прямая теорема кодирования с заданным критерием качества
- •4.11. Аксиоматическое введение в теорию энтропии вероятностных схем
- •4.12. Энтропия и условная энтропия объединенной вероятностной схемы и их свойства
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
4.12. Энтропия и условная энтропия объединенной вероятностной схемы и их свойства
В этом параграфе определены понятия энтропии объединённой вероятностной схемы, условной энтропии; доказана важная теорема о связи энтропии объединённой вероятностной схемы и энтропии составляющих её частных схем.
Рассмотрим вероятностные схемы:
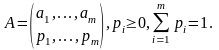 (4.40)
(4.40)
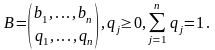 (4.41)
(4.41)
Вообще
говоря, схемы А,
В
не предполагаются независимыми, то есть
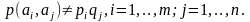 p(ai,bj)
p(ai,bj)
Определение.
Назовем схему С
- объединённой вероятностной схемой с
множеством исходов
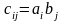 и вероятностным распределением
и вероятностным распределением
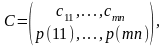 (4.42)
(4.42)
если для вероятностей p(ij) выполняются следующие соотношения:
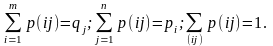
Для объединённой вероятностной схемы будем использовать обозначение С = АВ.
Понятие объединённой вероятностной схемы естественным образом распространяется на произвольное конечное множество конечных вероятностных схем.
Для простоты записи для условных вероятностей будем использовать следующие обозначения:
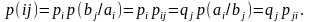
Определение. Энтропией объединённой вероятностной схемы AB называется величина:
 (4.43)
(4.43)
Преобразуем выражение Н(АВ):
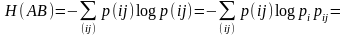
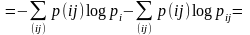
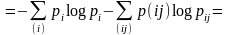
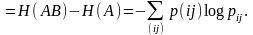
Отсюда следует
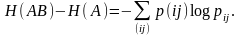 (4.44)
(4.44)
Определение. Величина
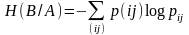 (4.45)
(4.45)
называется условной энтропией вероятностной схемы B относительно схемы A.
В (4.42) вероятностные схемы А и В при необходимости можно рассматривать как объединённые схемы.
Наряду
с энтропией
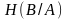 вводят следующую условную энтропию:
вводят следующую условную энтропию:
Определение. Величина
 (4.46)
(4.46)
называется
условной энтропией вероятностной
схемы B
относительно исхода
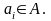
Имеет место:
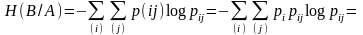
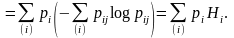
Полученное равенство дает основание назвать энтропию средней условной энтропией.
Формула (4.44) может быть переписана в новых обозначениях следующим образом:
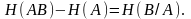 (4.44')
(4.44')
Если
вероятностные схемы А и В статистически
независимы, то есть
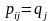 то:
то:
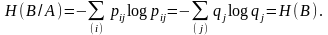
Аналогично можно ввести условную энтропию . Докажем важное соотношение между энтропией объединённой вероятностной схемы и энтропиями составляющих схем.
Теорема. Для любых двух конечных вероятностных схем справедливо неравенство:
 (4.47)
(4.47)
Равенство в (4.47) имеет место тогда и только тогда, когда схемы А и В независимы.
Доказательство.
Обозначим
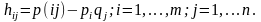 Заметим, что:
Заметим, что:
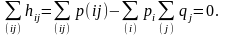
Пусть f (x) - непрерывная на [x, x + h] функция, имеющая конечную производную в каждой точке интервала (х, х + h) (h ≥ 0). По теореме Лагранжа о конечных приращениях получаем:
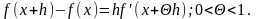
Положим
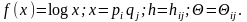
Тогда имеем:
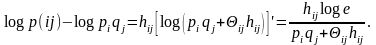
Соотношение
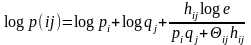
усредним по вероятностной схеме АВ и умножим на (-1):

Оценим разность:
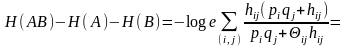
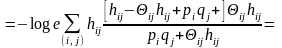

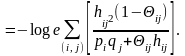
Так
как
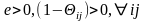 ,
то знак суммы определяется знаком
знаменателя в каждом слагаемом.
,
то знак суммы определяется знаком
знаменателя в каждом слагаемом.
При
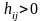 знаменатель положителен. Если
знаменатель положителен. Если
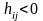 ,
то
,
то

Следовательно, рассматриваемая разность отрицательна. Откуда вытекает, что:
Если схемы независимы, то
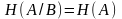 и
и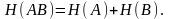
Докажем
обратное утверждение, если
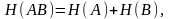 то это возможно, когда
то это возможно, когда
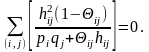
Так
как каждое слагаемое неотрицательно,
то равенство этой суммы нулю возможно
тогда, когда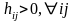 .
То есть
.
То есть
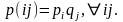 Это и означает статистическую независимость
вероятностных схем А и В. Замечание.
Используя неравенство
Это и означает статистическую независимость
вероятностных схем А и В. Замечание.
Используя неравенство
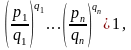 где
где
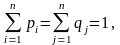 (4.48)
(4.48)
можно легко получить ещё одно доказательство теоремы 1.2.1. Прологарифмируем обе части неравенства:
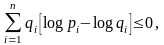
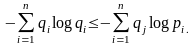 (4.49)
(4.49)
Заметим, что:
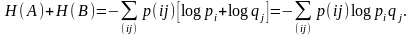
В силу неравенства (4.49) получаем:

Замечание. Доказательство теоремы может быть получено с использованием неравенства:
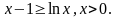 (4.50)
(4.50)
Рассмотрим:
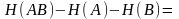

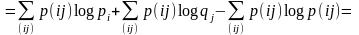
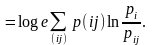
Сумма в последнем соотношении берётся по тем (i, j), для которых p(ij) > 0.
Для
этих слагаемых
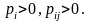
Следовательно, неравенство (4.50) может быть применено для каждого слагаемого
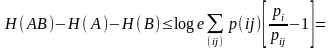
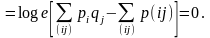
Приведём ряд следствий, вытекающих из теоремы 1.
1°
 (4.51)
(4.51)
Доказательство.
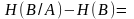

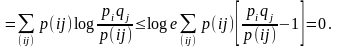
2°
Неравенство (4.51) остается справедливым
и в случае, когда
 - объединённая вероятностная схема.
- объединённая вероятностная схема.
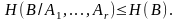 (4.52)
(4.52)
Доказательство.
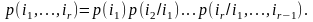
Прологарифмируем полученное равенство:
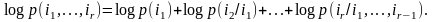
Умножим
это соотношение на
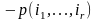 и просуммируем по вероятностной
схеме
и просуммируем по вероятностной
схеме
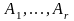 :
:
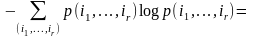
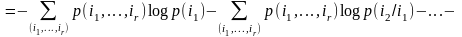

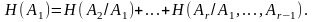
В силу следствий 1° и 2°:
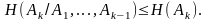
Следовательно, неравенство (4.52) доказано.
4° Для любых трёх конечных вероятностных схем А, В, С справедливо неравенство
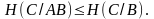
Доказательство.
Предположим, что реализовалось событие
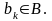
Апостериорное распределение в схемах АС, А, С обозначим:
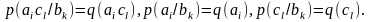
Наряду со схемами А, С, АС введём и схемы А', С', (АС)' с апостериорным распределением.
Из следствия 1° имеем:
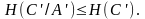 (4.53)
(4.53)
В терминах условных энтропии перепишем (4.53) следующим образом:
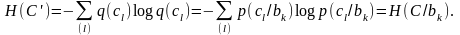
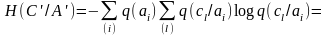
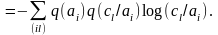
Выразим
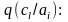
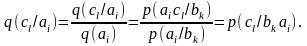
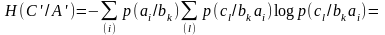
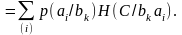
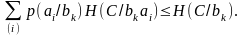 (4.53')
(4.53')
Умножая обе части равенства (4.53') на р(bk) и суммируя по вероятностной схеме В, имеем:
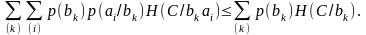
то есть
5°
Для любых г конечных вероятностных схем
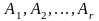 справедливо неравенство:
справедливо неравенство:
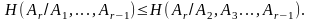 (4.54)
(4.54)
Результаты, изложенные в данном параграфе, используются для получения соответствующих энтропийных оценок.
