4.11. Аксиоматическое введение в теорию энтропии вероятностных схем

Исходным понятием для построения рассматриваемой теории является по­нятие вероятностной схемы. Пусть (Ω, М, Р) - вероятностное пространство, {a_j}- полная группа попарно несовместимых событий.

Определение 1. Пара А = ({a_j},(p(a_j))) называется вероят­ностной схемой.

Говорят, что вероятностная схема А дискретна, если число событий {a_j}не более чем счётно. В этом случае А будем записывать в виде:

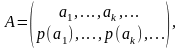(4.34)

где а_к - исход вероятностной схемы, р(а_к) - вероятность исхода,

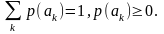
Если число событий {а_к} более чем счётно, то вероятностная схема А на­зывается непрерывной. Тогда её задают, описывая множество возможных ис­ходов и указывая с помощью плотности распределения вероятностей р(х) ве­роятностное распределение на исходах. На протяжении данного курса будем, как правило, рассматривать конечные вероятностные схемы.

Важной характеристикой схемы является энтропия - средняя мера нерав­новероятности исходов схемы. Энтропия и близкое понятие информация по-разному определялись рядом авторов. Приведём некоторые из этих определений.

Согласно Р. Хартли количество информации, содержащееся в сообщении, должно удовлетворять двум требованиям:

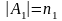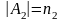а. Пусть сообщение Т₁, записанное в алфавите A₁, имеет длину l₁ а сообщение Т₂, записанное в алфавите А₂, , имеет длину l₂. Тогда если выполнено 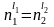, то сообщения Т₁ и Т₂ несут одина­ковое количество информации.

b. Количество информации, содержащееся в сообщении, пропорционально его длине.

Из этих положений Хартли получил формулу для количества информации в сообщении:

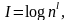(4.35)

где n=|А| - мощность алфавита, l - длина сообщения.

К. Шеннон рассматривал порождение сообщений в условиях вероятностной схемы:

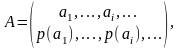
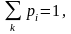
Относительно количества информации, содержащегося в сообщении Т дли­ны l составленном по схеме независимых испытаний, высказываются сле­дующие требования:

a. Пустое сообщение не содержит информации.

b. Количество информации, содержащееся в сообщении, пропорционально его длине.

По Шеннону, количество информации, содержащееся в сообщении 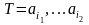равно:

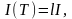(4.36)

где 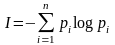- энтропия вероятностной схемы, или количество информации, приходящееся на один символ порождённого сообщения.

Величина а (а > 1) - основание логарифмов, определяет единицу измерения количества информации. Если а = 2, то информацию измеряют в двоичных единицах битах; если а = е, то информация измеряется в натуральных еди­ницах натах; если а = 10, то информация измеряется в десятичных единицах дитах.

А. Я. Хинчин к определению энтропии вероятностной схемы подошёл с ак­сиоматических позиций. В его работе установлено, что энтропия конечной вероятностной схемы однозначно определяется с точностью до постоянного множителя при задании системы аксиом.

Аксиомы Хинчина

1. 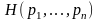- ненулевая непрерывная по переменным 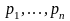в симплексе

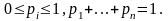
2. - симметрична по переменным .

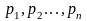3. .

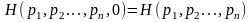4.

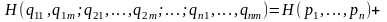
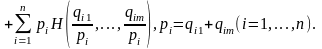
5.

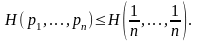
Система аксиом Фаддеева эквивалентна системе аксиом Хинчина и позволяет получить тот же результат.

Аксиомы Фаддеева

1'. 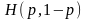непрерывна при 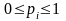и положительна хотя бы в одной точке.

2'. 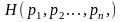симметрична по .

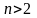
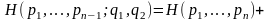
3'. При 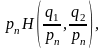где

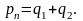
Разница в этих системах аксиом заключается в том, что аксиома 5 (экст­ремальность функции энтропии) заменяется требованием положительности энтропии в одной точке. Аксиомы Хинчина 3 и 4 заменяются аксиомой 3'. Аксиома 3' естественна, так как неопределённость схемы

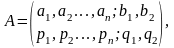
отличается от неопределённости схемы

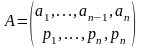
на неопределённость, происходящую от подразделения а_n на два подсобытия b₁,b₂ с условными вероятностями 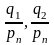. Эта неопределённость должна быть преодолена только в случае, если реализуется событие а_n, вероятность которого равна р_n.

Если рассматривать энтропию как количественную меру неопределённости в реализации вероятностной схемы, то последняя аксиома естественна.

Установим равносильность аксиом 2, 3, 4 и 2', 3', сле­дуя упомянутой работе Фаддеева.

Лемма 1. Из аксиом 2, 3, 4 следует, что .

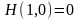Доказательство.

Подсчитаем 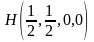двумя способами:

По аксиоме 3:

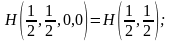
По аксиоме 2:

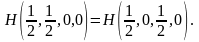
Применим аксиому 4:

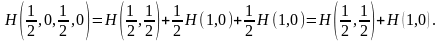
Отсюда следует, что

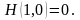
Лемма 2. Из аксиом 2, 3, 4 следует аксиома 3'.

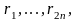
Доказательство. Рассмотрим набор 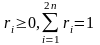среди 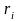есть 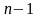нуль. Из аксиом 2 и 3 следует, что 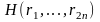перестановка­ми аргументов можно представить в виде:

.

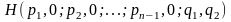Применим аксиому 4:

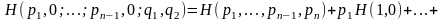
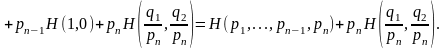Лемма 3. Из аксиом 2', 3' следует, что Н(1,0) = 0.

Доказательство. Подсчитаем двумя способами

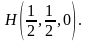
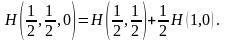
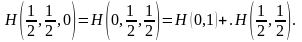
Следовательно, Н(1,0) = 0.

Лемма 4. Из аксиом 2', 3' следует аксиома 3.

Доказательство.

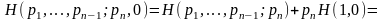
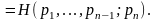
Лемма 5. Из аксиомы 3' следует

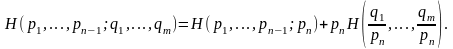
Здесь m > 2,

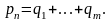
Доказательство. При m = 2 утверждение леммы совпадает с аксиомой 3'. При 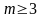лемма доказывается индукцией по m.

Лемма 6. Из аксиом 2', 3' следует

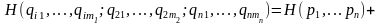
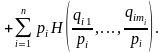
Здесь

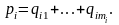
Доказательство. Нужно n раз применить лемму 5 к каждой группе ар­гументов, что возможно в силу симметрии. Приняв m₁ = m₂ = ... = m_n = m, по­лучим, что из аксиом 2', 3' следует аксиома 4.

Установлена равносильность групп аксиом 2, 3, 4 и 2', 3'.

Перейдём к доказательству теоремы единственности функции энтропии. Введём определение:

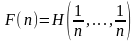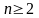, при и

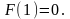
Применяя лемму 6 к случаю m₁ = m₂ = ... = m_n = m 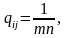получим

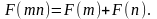(4.37)

Применим лемму 5 к :

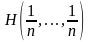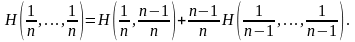
Обозначим

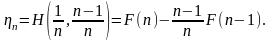
Лемма 7. Пр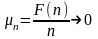и

и

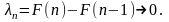
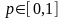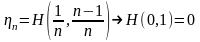Доказательство. В силу непрерывности при .

при

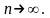
Далее,

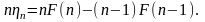
Отсюда, складывая эти соотношения для 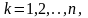k = 1,2.., имеем:

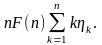
Получаем

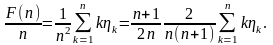
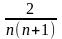
Однако 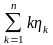- среднее арифметическое первых 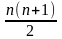членов стремящейся к нулю последовательности

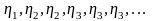
Следовательно,

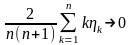и , при

Далее,

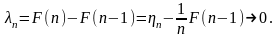Лемма доказана.

В силу формулы (4.37) функция F(n) будет определена при всех натураль­ных n, как только зададим значения функции F на простых числах.

Именно, если n, где 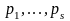- простые, то

.

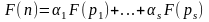Положим,

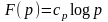, где p - простое число. (4.38)

Тогда

Лемма 8. Среди чисел с_р (р = 2,3,5,7,...) существует наибольшее.

Доказательство. Допустим противное и покажем, что это предположение противоречит предположению о непрерывности 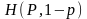при р = 0. Действительно, если в последовательности с_р (р = 2,3,5,7,...) нет наибольшего числа, то можно построить бесконечную последовательность простых чисел 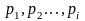так, что 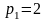, р_i - есть наименьшее простое число, такое, что c_pi > c_pi-1. Из способа построения этой последовательности ясно, что как только простое число q меньше р_i, то c_q < с_рi .

Пусть i > 1 и 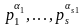есть каноническое разложение числа .

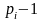Рассмотрим

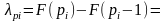
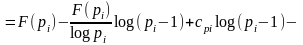
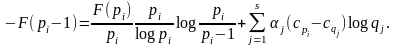
Ясно, что

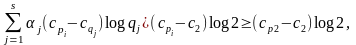
так как 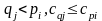и в силу чётности (p_i - 1) среди q_j присутствует число 2 с ненулевым показателем.

Далее, при i →

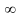
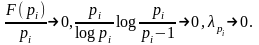
Следовательно,

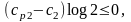что невозможно.

Таким же образом устанавливается, что среди с_р существует наименьшее.

Лемма 9. Функция 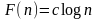, где с - постоянное. Доказательство. Достаточно установить, что все с_р равны друг другу. До­пустим, что найдётся такое простое число р’ что c_р' > c₂. Обозначим через р то простое число, для которого с_р принимает наибольшее значение. Тогда c_р > c₂ и р > 2.

Пусть m - натуральное число и 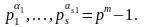Рассмотрим:

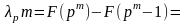
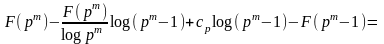
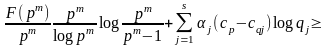
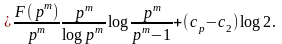
При переходе к пределу при 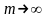получим 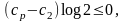0, что невоз­можно. Таким образом, для всех р' имеет место

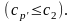
Совершенно таким же образом устанавливается, что 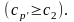при всех р’ Лемма доказана.

С учётом доказанных лемм 7, 8, 9 в системе аксиом Фаддеева может быть доказана:

Теорема 1. Справедливо представление функции :

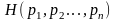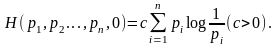(4.39)

Доказательство. Рассмотрим случай n = 2

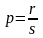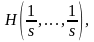Пусть - при натуральных г и s. Применим лемму 1.1.6 к соединив аргументы в две группы из r и s - r элементов. Получим:

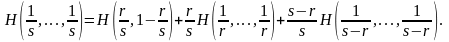
Отсюда

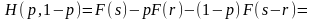
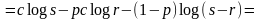
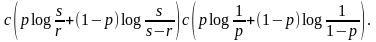
В силу непрерывности Н(р,1 - р) полученная формула может быть распрост­ранена и на иррациональные значения р. Постоянная С > 0 в силу положи­тельности Н(р ,1- р), хотя бы в одной точке.

Переход к общему случаю осуществляется методом математической индук­ции на основании аксиомы 3'.

Выводы этой фундаментальной теоремы Д. К. Фаддеева о представлении функции энтропии для дискретной вероятностной схемы позволят в дальней­шем характеризовать производительность источника информации, оценивать возможности сжатия информации, получить формулу для вычисления про­пускной способности дискретного канала связи.