
- •Введение
- •1. Энтропия источников сообщений
- •1.1. Дискретные ансамбли и источники
- •1.2. Количество информации в дискретном сообщении. Энтропия ансамбля
- •1.3. Условная информация. Условная энтропия. Совместная энтропия дискретного источника
- •1.4. Энтропия дискретного стационарного источника на сообщение
- •1.5. Избыточность источника дискретных сообщений
- •1.6. Эффективное кодирование. Кодирование источника равномерными кодами
- •1.7. Высоковероятные множества постоянного дискретного источника
- •1.8. Энтропия источника без памяти как скорость создания информации
- •1.9. Избыточность источника непрерывных сигналов. Количество информации в непрерывном канале
- •1.10. Скорость передачи информации и пропускная способность в непрерывном канале
- •2. Кодирование информации
- •2.1. Неравномерное кодирование с однозначным декодированием
- •2.2. Оптимальные неравномерные двоичные коды
- •2.3. Кодирование для исправления ошибок: Основные положения
- •2.4. Постановка задачи кодирования
- •2.5. Прямая теорема о кодировании в канале с шумами
- •2.6. Обратная теорема кодирования
- •2.7. Основная теорема Шеннона, ограничение возможностей использования оптимального кодирования на практике
- •3. Коды, исправляющие ошибки
- •3.1. Блоковые и сверточные коды
- •3.2. Хеммингово расстояние, Хемминговы сферы и корректирующая способность
- •3.3. Линейные блоковые коды
- •3.4. Порождающая и проверочная матрицы. Кодирование с помощью матриц g и н
- •3.5. Декодирование по стандартной таблице
- •3.6. Циклические коды
- •3.7. Кодирующие устройства циклических кодов
- •3.8. Декодирование циклических кодов по синдрому
- •3.9. Мажоритарное декодирование
- •4. Энтропия в контексте защиты информации от помех при передаче по каналу связи
- •4.1. Меры искажения. Постановка задачи защиты информации от помех при передаче по каналу связи
- •4.2. Свойства функции скорость-искажение
- •4.3. Простые примеры вычисления функции скорость-искажение
- •4.4. Функция скорость-искажение для гауссовских последовательностей
- •4.5. Эпсилон-производительность источника
- •4.6. Дифференциальная энтропия
- •4.7. Свойства дифференциальной энтропии
- •4.8. Эпсилон - энтропия источника сообщений
- •4.9. Обратная теорема кодирования для дискретного постоянного источника при заданном критерии качества
- •4.10. Прямая теорема кодирования с заданным критерием качества
- •4.11. Аксиоматическое введение в теорию энтропии вероятностных схем
- •4.12. Энтропия и условная энтропия объединенной вероятностной схемы и их свойства
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
4.5. Эпсилон-производительность источника
Если
источник выдает независимые отсчеты
сигнала Х(t)
в дискретные моменты времени со скоростью
 ,
где интервал дискретизации
,
где интервал дискретизации
 (
– полоса частот сигнала X(t)),
то эпсилон-производительность источника
(эпсилон-энтропия, приходящаяся на
единицу времени)
(
– полоса частот сигнала X(t)),
то эпсилон-производительность источника
(эпсилон-энтропия, приходящаяся на
единицу времени)
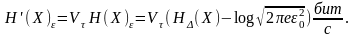 (4.11)
(4.11)
Если время непрерывное, то
 (4.12)
(4.12)
Максимальное значение эпсилон-производительность источника имеет, когда сигнал X(t) является гауссовским (4.19):
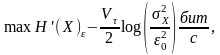 (4.13)
(4.13)
 (4.14)
(4.14)
За время Т существования сигнала максимальный объем V информации, выданной источником, составит
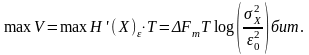 (4.15)
(4.15)
Объем сигнала – это максимальное количество информации, которое сигнал может переносить.
4.6. Дифференциальная энтропия
Источники информации, множество возможных состояний которых составляют континуум, называют непрерывными.
Во многих случаях они преобразуются в дискретные посредством использования устройств дискретизации и квантования. Вместе с тем существует немало и таких систем, в которых информация передаётся и преобразуется непосредственно в форме непрерывных сигналов. Примерами могут служить системы телеизмерений с частотным разделением сигналов.
Основные информационные характеристики источников непрерывных сообщений следующие: энтропия, условная энтропия, эпсилон-энтропия, эпсилон-производительность, избыточность, объём информации.
Формулу для энтропии источника непрерывных сообщений получают путем предельного перехода из формулы для энтропии дискретного источника. С этой целью разобьём диапазон изменения непрерывной случайной величины Х, характеризующейся плотностью распределения вероятностей W(X), на конечное число m малых интервалов шириной Δx.
При
реализации любого значения х,
принадлежащего интервалу [xi,
xi+Δx],
будем считать, что реализовалось значение
xi
дискретной
случайной величины Х.
Поскольку Δx
мало,
то вероятность
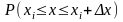 реализации
значениях
из
интервала [xi,
xi+Δx],
равна
реализации
значениях
из
интервала [xi,
xi+Δx],
равна
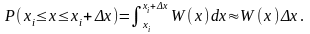
Тогда энтропия дискретной случайной величины X может быть записана в виде
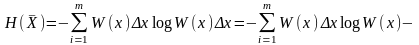

так
как
 .
.
По
мере уменьшения
 все больше приближается к вероятности
P(xi),
равной нулю, а свойства дискретной
величины
все больше приближается к вероятности
P(xi),
равной нулю, а свойства дискретной
величины
 –
к свойствам непрерывной случайной
величины Х.
–
к свойствам непрерывной случайной
величины Х.
В
результате предельного перехода при
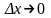 получено
получено
 (4.16)
(4.16)
Первый
член выражения (4.16) зависит только от
закона распределения непрерывной
случайной величины Х
и
имеет такую же структуру, как энтропия
дискретного источника. Второй член
 стремится
к бесконечности, это полностью
соответствует интуитивному представлению
о том, что неопределенность выбора из
бесконечно большого числа возможных
состояний (значений) бесконечно велика.
стремится
к бесконечности, это полностью
соответствует интуитивному представлению
о том, что неопределенность выбора из
бесконечно большого числа возможных
состояний (значений) бесконечно велика.
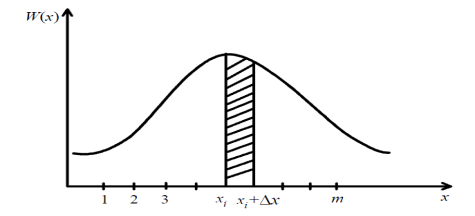
Рис. 4.6. Зависимость плотности распределения вероятностей случайной величины
Чтобы
избавить теорию от бесконечности,
имеется единственная возможность –
ввести относительную меру неопределенности
исследуемой непрерывной случайной
величины Х
по
отношению к заданной Х0
. В качестве заданной величины Х0
возьмем непрерывную случайную величину,
равномерно распределенную на интервале
с шириной
 .
Тогда её плотность вероятности W(X0)
=
1/е,
а энтропия
.
Тогда её плотность вероятности W(X0)
=
1/е,
а энтропия
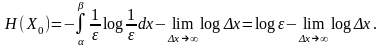
Положив для простоты записи = 1, составим разность
 (4.17)
(4.17)
которая
показывает, насколько неопределенность
непрерывной случайной величины Х
с
законом распределения W(X)
больше [ ]
или
меньше
]
или
меньше
 неопределенности
случайной величины, распределенной
равномерно на интервале
=
1. Поэтому величину
неопределенности
случайной величины, распределенной
равномерно на интервале
=
1. Поэтому величину
 (4.18)
(4.18)
называют
относительной дифференциальной энтропией
или просто дифференциальной энтропией
непрерывного источника информации
(непрерывного распределения случайной
величины Х).
В отличие от энтропии источников
дискретных сообщений
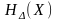 может
принимать положительные, отрицательные
и нулевые значения. Величиной
можно
характеризовать информационные свойства
источников непрерывных сообщений.
может
принимать положительные, отрицательные
и нулевые значения. Величиной
можно
характеризовать информационные свойства
источников непрерывных сообщений.
Аналогично, используя операции квантования и предельного перехода, найдем выражение для условной энтропии непрерывного источника сообщений.
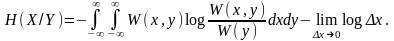 (4.19)
(4.19)
Обозначим
первый член через

 (4.20)
(4.20)
Эта величина конечна и называется относительной дифференциальной условной энтропией, или просто дифференциальной условной энтропией непрерывного источника. Она характеризует неопределенность выбора непрерывной случайной величины Х при условии, что известны результаты реализации значений другой статистически связанной с ней непрерывной случайной величины Y, и по сравнению со средней неопределенностью выбора случайной величины Х0, изменяющейся в диапазоне, равном единице, и имеющей равномерное распределение вероятностей.
