
- •Введение
- •1. Энтропия источников сообщений
- •1.1. Дискретные ансамбли и источники
- •1.2. Количество информации в дискретном сообщении. Энтропия ансамбля
- •1.3. Условная информация. Условная энтропия. Совместная энтропия дискретного источника
- •1.4. Энтропия дискретного стационарного источника на сообщение
- •1.5. Избыточность источника дискретных сообщений
- •1.6. Эффективное кодирование. Кодирование источника равномерными кодами
- •1.7. Высоковероятные множества постоянного дискретного источника
- •1.8. Энтропия источника без памяти как скорость создания информации
- •1.9. Избыточность источника непрерывных сигналов. Количество информации в непрерывном канале
- •1.10. Скорость передачи информации и пропускная способность в непрерывном канале
- •2. Кодирование информации
- •2.1. Неравномерное кодирование с однозначным декодированием
- •2.2. Оптимальные неравномерные двоичные коды
- •2.3. Кодирование для исправления ошибок: Основные положения
- •2.4. Постановка задачи кодирования
- •2.5. Прямая теорема о кодировании в канале с шумами
- •2.6. Обратная теорема кодирования
- •2.7. Основная теорема Шеннона, ограничение возможностей использования оптимального кодирования на практике
- •3. Коды, исправляющие ошибки
- •3.1. Блоковые и сверточные коды
- •3.2. Хеммингово расстояние, Хемминговы сферы и корректирующая способность
- •3.3. Линейные блоковые коды
- •3.4. Порождающая и проверочная матрицы. Кодирование с помощью матриц g и н
- •3.5. Декодирование по стандартной таблице
- •3.6. Циклические коды
- •3.7. Кодирующие устройства циклических кодов
- •3.8. Декодирование циклических кодов по синдрому
- •3.9. Мажоритарное декодирование
- •4. Энтропия в контексте защиты информации от помех при передаче по каналу связи
- •4.1. Меры искажения. Постановка задачи защиты информации от помех при передаче по каналу связи
- •4.2. Свойства функции скорость-искажение
- •4.3. Простые примеры вычисления функции скорость-искажение
- •4.4. Функция скорость-искажение для гауссовских последовательностей
- •4.5. Эпсилон-производительность источника
- •4.6. Дифференциальная энтропия
- •4.7. Свойства дифференциальной энтропии
- •4.8. Эпсилон - энтропия источника сообщений
- •4.9. Обратная теорема кодирования для дискретного постоянного источника при заданном критерии качества
- •4.10. Прямая теорема кодирования с заданным критерием качества
- •4.11. Аксиоматическое введение в теорию энтропии вероятностных схем
- •4.12. Энтропия и условная энтропия объединенной вероятностной схемы и их свойства
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
4.3. Простые примеры вычисления функции скорость-искажение
Все определения и утверждения в предыдущем параграфе приводились для непрерывного источника, но в равной степени могли быть записаны для дискретного ансамбля и соответственно подобранного критерия качества.
Пример. Двоичный источник.
161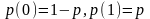 .
Источник порождает последовательности
независимых
одинаково распределенных двоичных
символов. Эти последовательности
аппроксимируются двоичными
последовательностями
.
Источник порождает последовательности
независимых
одинаково распределенных двоичных
символов. Эти последовательности
аппроксимируются двоичными
последовательностями
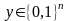 так, чтобы при заданной скорости
аппроксимирующего кода минимизировать
среднюю ошибку
так, чтобы при заданной скорости
аппроксимирующего кода минимизировать
среднюю ошибку
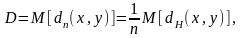
где -расстояние Хэмминга (число несовпадающих позиций вxи y.
В соответствии со свойством функцию скорость-искажение следует искать по формуле
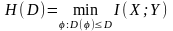
где
условные вероятности
задаются
всего двумя числами, например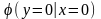 и
и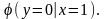 Хотя
поиск условного экстремума по этим двум
параметрам не кажется сверхсложной
задачей, мы не пойдем по этому
прямолинейному пути. Вместо этого мы
сначала найдем нижнюю оценку взаимной
информации, а затем покажем, что эта
оценка достижима при некотором
Хотя
поиск условного экстремума по этим двум
параметрам не кажется сверхсложной
задачей, мы не пойдем по этому
прямолинейному пути. Вместо этого мы
сначала найдем нижнюю оценку взаимной
информации, а затем покажем, что эта
оценка достижима при некотором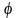 .
.
Введем
обозначение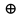 для операции сложения по модулю два и
заметим, что
для операции сложения по модулю два и
заметим, что
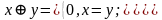 1,x
=y.
1,x
=y.
Это
означает, что ансамбль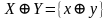 -
ансамбль ошибок при аппроксимации
источника Х
символами из Y.
При средней ошибке равной D
взаимную информацию
-
ансамбль ошибок при аппроксимации
источника Х
символами из Y.
При средней ошибке равной D
взаимную информацию
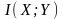 можно
оценить следующим образом:
можно
оценить следующим образом:
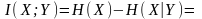

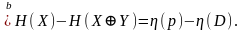 (4.2)
(4.2)
Здесь
в (а) замена Х
на
 при
условии Y
представляет собой детерминированное
преобразование и поэтому не меняет
энтропии. Неравенство (b)
имеет место потому, что условная энтропия
не может быть больше безусловной, и
при
условии Y
представляет собой детерминированное
преобразование и поэтому не меняет
энтропии. Неравенство (b)
имеет место потому, что условная энтропия
не может быть больше безусловной, и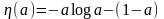 -
двоичная энтропия.
-
двоичная энтропия.

Рис. 4.2. Совместное распределение X и Y для двоичного источника
Предполагая, что получено правильное выражение для функции скорость-искажение, подберем к заданному ансамблю источника Х такой источник Y, для которого неравенства в можно заменить на точные равенство. Такая пара ансамблей показана на рисунке 4.2.
Положим
вероятности аппроксимирующих символов
равными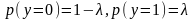 .
Вероятности символов
известны:
.
Вероятности символов
известны:
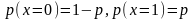 .
Условные вероятности
выбраны исходя из
требований к ошибке:
.
Условные вероятности
выбраны исходя из
требований к ошибке:
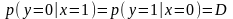 .
Поэтому неизвестный параметр
.
Поэтому неизвестный параметр
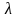 находим из уравнения
находим из уравнения
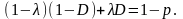
Решением является
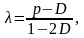
Теперь заметим, что приD = min{p, 1 —p} правая часть обращается в нуль. Это легко объяснить. Среднюю ошибку, равную этой величине можно получить, всегда используя в качестве аппроксимирующего символа один и тот же символ 0 либо 1, в зависимости от того, вероятность какого из них больше.
Итак, ансамбль, на котором достигается нижняя граница найден и тем самым найдена функция скорость-искажения. При этом мы так и не указали в явном виде функцию на которой достигается минимум взаимной информации. При желании эту функцию можно легко получить, воспользовавшись рисунком 4.2.
Сформулируем полученный в этом примере результат в виде теоремы.
Теорема. Функция скорость-искажение двоичного источника независимых символов с вероятностью единицы равной р при вероятностной мере искажения равна
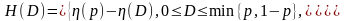 (4.3)
(4.3)
Типичный график H(D) для двоичного источника показан на рисунке 4.3.

Рис. 4.3. Функция скорость-искажение для двоичного источника
Пример. Гауссовский источник
Рассмотрим
последовательность независимых одинаково
распределенных гауссовских с.в. с
нулевым математическим ожиданием и
дисперсией
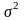 ,
т.е. с плотностью
,
т.е. с плотностью
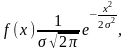
и вычислим функцию скорость-искажение при квадратическом критерии качества. Как и в предыдущем примере, начнем с вывода нижней границы на взаимную информацию, а потом убедимся, что граница достижима. Итак, по аналогии с двоичным источником
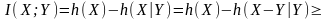
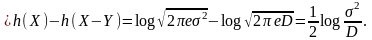 (4.4)
(4.4)
Здесь использована формула дифференциальной энтропии гауссовского ансамбля из таблицы и то, что гауссовское распределение имеет наибольшую энтропию среди всех распределений с заданной дисперсией.
Чтобы
доказать достижимость границы (4.4),
введем с.в.Z
=X
— Yи
будем считать ее гауссовской с нулевым
математическим ожиданием и дисперсиейD.
Поскольку сумма независимых гауссовских
с.в. есть гауссовская с.в. с суммарной
дисперсией, дисперсияX
=Y
+Z
равна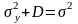 .
Нетрудно видеть, что пара случайных
величин X
иY
удовлетворяет (4.4) с равенством.
.
Нетрудно видеть, что пара случайных
величин X
иY
удовлетворяет (4.4) с равенством.
Приведенные
рассуждения имеют смысл только при
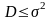 .
Поскольку значение
.
Поскольку значение
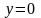 аппроксимирует
значения с.в. Х
со средней ошибкой
,
то при
функция
скорость-искажение тождественна равна
нулю.
аппроксимирует
значения с.в. Х
со средней ошибкой
,
то при
функция
скорость-искажение тождественна равна
нулю.
Теорема. Функция скорость-искажение источника независимых гауссовских с.в. с дисперсией при квадратическом критерии качества равна
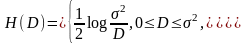 (4-28)
(4-28)
Иногда удобнее записывать в виде
 (4.29)
(4.29)
График функции скорость-искажение для гауссовского источника с единичной дисперсией показан на рис. 4.4.
Попутно с доказательством Теоремы нами установлена оценка снизу функции скорость-искажение произвольного стационарного источника, порождающего независимые сообщения ). Эту оценку часто называют границей Шеннона.
Следствие (Граница Шеннона). Функция скорость-искажение источника независимых с. в. с дисперсией и дифференциальной энтропией h(X) при квадратическом критерии качества удовлетворяет неравенству
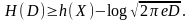
(4.30)

Рис. 4.4. Функция скорость-искажение для гауссовского источника
