8.2. Методы оптимизации циклов

Неудачное построение цикла приводит к значительному снижению быстродействия программы, поэтому широко используется оптимизация циклов. Самый простой прием оптимизации – вынесение из цикла тех переменных, которые в нем не модифицируются.

Например,

sum = 0; for (i = 1; i<1000; i++) sum += a * (x+i);	sum = 0; for (i = 1; i<1000; i++) sum += (x+i); sum*=a;
Медленнее	Быстрее

Методы оптимизации циклов:

• развертка циклов (loop unrolling),

• объединение циклов (loop fusion),

• разрезание циклов (loop distribution),

• выравнивание циклов (loop alignment),

• перестановка циклов (loop interchange),

• разделение на блоки (loop blocking).

Сопоставление

for ( int j = 0; j< 100000; j++) (for int k = 0; k< 1000; k++) a=1;	for ( int k = 0; j< 1000; k++) (for int j = 0; k< 100000; j++) a=1;
Медленнее, так как внутренний счетчик инициализируются 10001 раз	Быстрее, так как внутренний счетчик инициализируются 1001 раз

При программировании вложенных циклов по возможности следует делать цикл с наибольшим числом повторений самым внутренним, а цикл с наименьшим числом повторений — самым внешним.

Также следует отметить, что время выполнения цикла со счетчиком и цикла с постусловием при всех прочих равных условиях совпадает, цикл с предусловием выполняется дольше.

8.3. Примеры использования вложенных циклов

Пример 1. Программа составления таблицы умножения

void main()

{

int row, col;

puts (“\t Таблица Пифагора\n”);

for (row=1;row<=10;row++)

{

for (col=1;col<=10;col++)

printf(“%5d”, row*col);

printf(“\n”);}}

Пример 2. Программа рисования прямоугольного треугольника, заполненного заданным пользователем символом

void main()

{

char paint;

puts (“\t Введите символ\n”);

scanf(“%c”,&paint);

for (int i=0;i<5;i++)

{

for (int k=0;k<=i;k++)

putchar(paint);

putchar(‘\n’);

}

getchar();

}

Пример 3. Модификация программы поиска заданной цифры во введенном числе для повторного выполнения по желанию пользователя

#include <stdio.h>

#include <stdlib.h>

#include <locale.h>

int main(void)

{

long long int i;

char a;

while(1)

{

setlocale(0, "Russian");

puts("введите число");

scanf("%lld", &i);

getchar();

while (i!=0)

{

if (i % 10 == 5)

{

printf("Да, цифра 5 имеется в числе\n");

break;

}

i = (int)(i / 10);

}

if (!i) printf("Нет, цифры 5 не имеется в числе\n");

printf("Продолжить?(Да - y, нет -n)");

if ((a=getchar())=='n') break;

}

system("pause");

}

8.4. Практические задания

1. Напишите программу вычисления функции sin с заданной точностью eps.

Математическая модель решения – разложение функции синус в ряд Тейлора имеет вид:

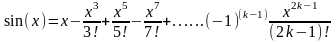
При решении важно понимать, что чем больше членов ряда будет просуммировано, тем точнее будет вычислен синус. Так если приемлемая точность равна eps, то достаточно суммировать члены ряда до тех пор, пока очередной член ряда не окажется меньше eps.

Для решения этой задачи следует использовать метод накопления, когда формирование следующего члена ряда осуществляется на основе предшествующего. В данном случае для получениеk-го члена ряда нужно (k-1)-й член умножить на x*x, разделить на k*(k-1). Это позволяет исключить использование функции возведения в степень и явное вычисление факториала в каждой итерации.

Следует также обратить внимание, что ряд – знакопеременный, т.е. в одной итерации значение прибавляется, а в следующей вычитается. Для такого случая применим прием, известный как «мерцающий счетчик», когда выделяется переменная и ее значение в каждой итерации умножается на (-1), таким образом чередуются отрицательные и положительные значения.

А) Оформите приглашение к вводу значения eps и инициализацию значения:

doubl eeps=1e-5;

Б) Организуйте цикл вычислений (ak – член ряда, sum – текущее значение ряда, k – счетчик итераций)

Инициализация:

ak=x; sum=ak; k=1;

Проверка условия:

fabs(ak)<eps;

Модификация:

k+=2; ak*=(-1)*x*x/(k*(k-1));

Тело цикла:

sum+=ak;

Для данной задачи можно выбирать любые конструкции построения цикла вычислений, но при выборе do-while будет иная инициализация переменных.

2. Дополните программу бесконечным циклом while() для повторения вычислений, пока пользователь задаст точность 0.

if(eps==0.) break;

3. Доработайте программу, чтобы она работала в трех режимах вычислений, включая

А) число итераций N задается пользователем;

Б)число итераций определяется из условия .

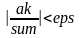4. Сопоставьте полученные результаты с библиотечной функцией sin(x).

Для этого проведите численный эксперимент, вводя различные значения точности eps,и вычислите погрешность, как разницу между значениями ряда и вычисленным с помощью библиотечной функции. Сделайте выводы.

5. Самостоятельно выполните приближенное вычисление ряда по заданным формулам:

№ вар.	Ряд	функция
1	1 – x2/ 2! + x4/4! + …+ (-1)n x2n/(2n)!	cos(x)
2	z=((x-1)/(x+1))   f(x)= (2/1)z + (2/3) z3 +...+ (2/2n-1)z2n-1	ln(x)
3	1+ x ln3 + (x ln3)2/2! +...+(x ln 3)n/n!	3x
4	(x-1)/x+(x-1)2/2x2+(x-1)3/3x3+…+(x-1)n/nxn	ln(x)
5	x + x3/3! + x5/5! +…+ x2n-1/(2n-1)!	sh(x)
6	1 + x2/2! + x4/4! +…+ x2n/(2n)!	ch(x)
7	x – x3/3 + x5/5 +…+ (-1)n+1x2n-1/(2n-1)	arctg(x)
8	π/2 – 1/x + 1/3x3 – 1/5x5 + (-1)n(2n-1)x2n-1	arctg(x)
9	x + x3*1/(2*3) + x5*(1*3)/(2*4*5) +… +x2n+1(1*3*…*2n-1)/(2*4*…2n(2n+1))	arcsin(x)
10	1+x(1/2)+x2(1*1)/(2*4)-x3(1*1*3)/(2*4*6)+… (-1)nxn(1*1*3*…*2n-3)/(2*4*6*…*2n)	(1+x)0.5
11	1-x(1/2)+x2(1*3)/(2*4)-x3(1*3*5)/(2*4*6)+… (-1)nxn(1*3*…*2n-1)/(2*4*…*2n)	1/(1+x)0.5
12	1+x/1!+x2/2!+x3/3! …xn/n!	eх