
- •Введение
- •Целевое назначение методов моделирования иб оз, его сиб
- •Сущность исследований иб оз различными методами
- •Глава 1. Парадигма системного моделирования информационной безопасности объектов защиты
- •1.1. Концепция системного математического моделирования информационной безопасности объектов защиты [52]
- •Основания для ветвления интегральной цели оз, его сиб на частные цели
- •1.2. Принципы системного математического моделирования информационной безопасности [53]
- •1.3. Методология системного математического моделирования информационной безопасности [50,51,57,61]
- •Сущность логико-вероятностно-информационного подхода к исследованиям иб оз, его сиб
- •Реализация сущности на основе введения лингвистической переменной и ветвления интегральной цели иб оз, его сиб на частные
- •1.4. Научно-методическое обеспечение системного моделирования информационной безопасности
- •Глава 2. Теоретические методы системного моделирования информационной безопасности
- •2.1. Парадигма исследований информационной безопасности теоретическими методами
- •Концепция [52]
- •Методология и алгоритмы системного моделирования иб [50,51]
- •Научно-методическое обеспечение системного моделирования иб [37,38]
- •Технология согласования интересов оз, его сиб с планетарными интересами
- •2.2. Системное синтаксическое моделирование информационной безопасности теоретическими методами
- •Типовые проблемные ситуации
- •Международные требования к информационному обеспечению устойчивости развития
- •Имена возможных состояний внешней среды оз, его сиб
- •2.3. Системное математическое моделирование информационной безопасности теоретическими методами
- •Концепция и принципы
- •Основания классификатора возможных состояний оз, его сиб
- •Основания классификатора типовых ситуаций
- •Методология и методы системного математического моделирования иб теоретическими методами
- •Моделирование исходов дуэли в статике
- •Моделирование исходов дуэли в динамике Концепция и принципы моделирования
- •Парадигма моделирования меры информации Концепция и принципы
- •Ассоциации меры информации с реально складывающейся обстановкой
- •Мера информации о логически связанных событиях: типовые ситуации
- •2.4. Научно-методическое обеспечение исследований информационной безопасности на системе моделей теоретическими методами
- •Принципы формирования сспэ
- •Концепция
- •Принципы и математические модели критериев оптимизации
- •Общий вывод
- •Проектов сиб
- •2.5. Парадигма управления циклами информационной и интеллектуальной поддержки защищённости объекта
- •Концепция
- •Принципы
- •Общий вывод
- •Законы и закономерности условно взаимосвязанного развития внешней и внутренней среды оз, его сиб
- •Глава 3. Эвентологические методы системного моделирования информационной безопасности
- •3.1. Парадигма исследований информационной безопасности эвентологическими методами
- •3.2. Эвентологические методы системного моделирования информационной безопасности
- •3.3. Введение начала отсчёта и градаций состояния защищённости эвентологическими методами
- •1, То это высота функции,
- •3.4. Принципы и критерии глобальной оптимизации кадровой политики в информационной сфере
- •Общий вывод
- •Заключение
- •Библиографический список источников Нормативно-правовые документы
- •Библиография
- •Содержание
- •394006 Воронеж, ул. 20-летия Октября, 84
Общий вывод
Цель защиты ОЗ, его СИБ достигается в результате комплексирования эффективных методов формирования панорамы опасных угроз априори (решение задач анализа ситуации) и адекватных им методов формирования панорамы защиты от угроз апостериори (решение задач синтеза), то есть по результатам проектирования облика ОЗ, его СИБ, программно-целевого планирования траектории их БУР(КСП(ИО(ИБ(ИК)))), их перепроектирования и перепрограммирования по ситуации и результатам на основе оптимизации и адаптации проектов и программ к реально складывающейся и прогнозируемой обстановке.
Введение принципов и адекватных им критериев оптимизации
Проектов сиб
Главным принципом
оптимизации способов и средств достижения
целей ОЗ, его СИБ является принцип
преемственности накопленной базы знаний
и ресурса по проблеме обеспечения их
ИБ, разумной достаточности дальнейшего
усовершенствования и развития этой
базы при ограниченном ресурсе.
Применительно к задаче оптимизации и
адаптации проектов облика СИБ и траектории
её устойчивого развития, согласно
методология решения векторных
многокритериальных задач с нормализованными
локальными критериями. требуется
сформировать вектор критериев Е = (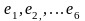 ),
где е
–
главный принцип. Задача состоит в том,
что необходимо выяснить, как отображаются
области определения возможных исходов
дуэли в типовых ситуациях в пространство
критериев, и выделить соответствующие
области
),
где е
–
главный принцип. Задача состоит в том,
что необходимо выяснить, как отображаются
области определения возможных исходов
дуэли в типовых ситуациях в пространство
критериев, и выделить соответствующие
области
 и
и
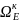 согласия и компромисса в пространстве
критериев. Решение такой задачи базируется
на реализации следующих шести принципов.
согласия и компромисса в пространстве
критериев. Решение такой задачи базируется
на реализации следующих шести принципов.
1. Принцип технико-экономической целесообразности, который базируется на соблюдения закономерностей экономического управления проектами по форме хозяйствования 5С и требовании: антикризисные инновационно-инвестиционные проекты должны быть малобюджетными, иметь короткий срок окупаемости и длительный срок полезной жизни, отличаться пониженными рисками, основываться на чётком и убедительном для сторонних инвесторов бизнес-плане. Сетевой график антикризисного проекта должен иметь критический путь, то есть такой, чтобы по всем остальным работам проекта оставались свободные ресурсы для манёвра по ситуации и результатам в статике и динамике.
2.
Принцип последовательных справедливых
относительных суммарных уступок
базируется на следующем утверждении:
справедливым является такой компромисс,
при котором суммарный относительный
уровень снижения качества,
 ,
одного или нескольких критериев не
превосходит суммарного относительного
уровня повышения качества по остальным
критериям:
,
одного или нескольких критериев не
превосходит суммарного относительного
уровня повышения качества по остальным
критериям:
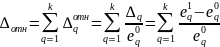 ,
(13),
,
(13),
где
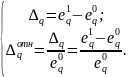 (14)
(14)
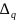 и
и
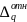 – величины абсолютной и относительной
уступки по локальному критерию
– величины абсолютной и относительной
уступки по локальному критерию
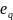 при переходе от значения
при переходе от значения
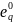 к
к
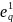 .
.
3. Принцип последовательных уступок в динамике базируется на утверждении: наилучшим, в смысле принципа суммарной относительной уступки является решение, соответствующее , если для любого другого решения из области компромиссов выполняется условие:
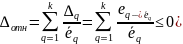 (для любого E
(для любого E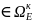 ).
(15)
).
(15)
В
оптимальной точке 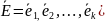 величина мультипликативной функции
величина мультипликативной функции
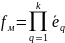 достигает максимального значения на
и критерий оптимизации имеет вид:
достигает максимального значения на
и критерий оптимизации имеет вид:
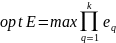 .
(16)
.
(16)
E E
Принцип относительной уступки чувствителен к величине критериев, так как за счет относительности уступки происходит автоматическое снижение её «цены» для локальных критериев с большой величиной и наоборот. Принцип инвариантен к масштабу измерения критериев.
Введение принципов и адекватных им критериев оптимизации проектов СИБ
4.
Принцип квазиравенства.
Идея равенства проводится приближённо
с точностью до некоторой величины
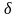 .
Решение считается наилучшим, если
значения отдельных локальных критериев
отличаются друг от друга не более чем
на величину
(допустимые,
критические И/ИЛИ неприемлемые ошибки
в оценке состояний ОЗ, его СИБ).
Соответствующий принцип оптимальности
можно представить в виде:
.
Решение считается наилучшим, если
значения отдельных локальных критериев
отличаются друг от друга не более чем
на величину
(допустимые,
критические И/ИЛИ неприемлемые ошибки
в оценке состояний ОЗ, его СИБ).
Соответствующий принцип оптимальности
можно представить в виде:
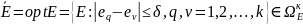 (17)
(17)
Е
Все решения, которые попали в область 2 (рис.25.), являются оптимальными в смысле принятого принципа оптимальности.
Неприемлемые ошибки ассоциируются с областью недопустимого состояния ОЗ, его СИБ адекватно требованиям по уровню защиты, которые отвечают законам защиты государственной военной, коммерческой и других видов тайн.
Допустимыми являются ошибки, которые ассоциируются с областью среднеквадратических ошибок для нормального закона распределения с центральной симметрией вероятности достижения цели ОЗ, его СИБ на заданном уровне защищённости.
Критические ошибки ассоциируются с координатами сопряжения перехода объекта из одной области определения его состояния в другое.
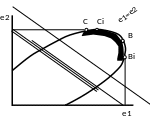
2
Рис. 25. Определение
области компромисса
5.
Принцип необходимого и достаточного
приближения реального и потенциально
возможного к необходимому неизбежно
связан с нормализацией локальных
критериев с учётом их приоритетов.
Нормализация базируется на
понятии идеального качества операции
(эталон, норма), представляемого вектором
идеальных значений критериев
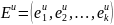 C
помощью
C
помощью
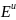 вектор критериев Е
приводится
к безразмерной (нормированной) форме:
вектор критериев Е
приводится
к безразмерной (нормированной) форме:
 (18)
(18)
Каждая
компонента вектора
принадлежит
диапазону [0; 1]
при условии, что все
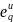 > 0. Успешное решение проблемы нормализации
зависит от
> 0. Успешное решение проблемы нормализации
зависит от
того насколько правильно и объективно удаётся определить «идеальное» качество решений, т.е. эталон (норму), полученный теоретическими и/или эффективными (эмпирическими) методами.
6. Принцип гибкого приоритета предназначен для реализации общего критерия оптимизации: необходимо «И» потенциально возможно «И реально достижимо ПРИ допустимых, критических И/ИЛИ неприемлемых ошибках. Фактически речь идёт о решении проблемы глобальной оптимизации на модели БУР(КСП(ИО(ИБ(ИК)))). Её решение неизбежно связано с нормализацией локальных критериев с учётом их приоритетов. Нормализация базируется на понятии идеального качества операции (эталон, норма), представляемого вектором идеальных значений критериев C помощью вектор критериев Е приводится к безразмерной (нормированной) форме:
(19)
Каждая компонента вектора принадлежит диапазону [0; 1] при условии, что все > 0. Успешное решение проблемы нормализации зависит от того насколько правильно и объективно удаётся определить «идеальное» качество решений, т.е. эталон (норму), полученный теоретическими и/или эффективными (эмпирическими) методами.
Математические методы оптимизации, адекватные комплексу принятых локальных критериев с учётом их приоритетов.
Принцип нормализации
локальных критериев.
В
качестве компоненты
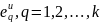 идеального вектора Еи
в нашем случае целесообразно принять
максимально возможный разброс
соответствующего локального критерия,
а именно:
идеального вектора Еи
в нашем случае целесообразно принять
максимально возможный разброс
соответствующего локального критерия,
а именно:
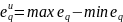 .
(20)
.
(20)
Тогда способ задания приоритетов локальных критериев базируется на построении их приоритетного ряда, I, с точки зрения возможностей достижения целей ОЗ, его СИБ. С этой целью вводятся: вектор приоритета
V=
(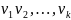 )
и
вектор весовых коэффициентов (весовой
вектор)
)
и
вектор весовых коэффициентов (весовой
вектор)
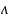 =
=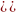 ),
т.е. их приоритетный ряд.
),
т.е. их приоритетный ряд.
А).
Ряд
приоритета I
отражает чисто качественные отношения
доминирования локальных критериев и
представляет собой упорядоченное
множество их индексов, с помощью которых
формируют приоритетный ряд:
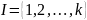 .
Среди таких критериев могут быть
равнозначные. Они берутся в квадратные
скобки. Например: [БУР, КСП, ИБ] ОЗ, его
СИБ.
.
Среди таких критериев могут быть
равнозначные. Они берутся в квадратные
скобки. Например: [БУР, КСП, ИБ] ОЗ, его
СИБ.
В).
Вектор
приоритета,
V=
(
).
Если
некоторые критерии
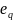 и
и
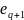 равнозначны,
то соответствующая компонента
равнозначны,
то соответствующая компонента
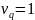 .
Для
удобства вычислений обычно полагают
.
Для
удобства вычислений обычно полагают
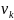 =1.
Вектор
приоритета V
определяется
в результате попарного
сравнения
локальных критериев, предварительно
упорядоченных в соответствии с рядом
приоритета I.
В этом случае любая компонента
вектора
приоритета
V
удовлетворяет соотношению:
=1.
Вектор
приоритета V
определяется
в результате попарного
сравнения
локальных критериев, предварительно
упорядоченных в соответствии с рядом
приоритета I.
В этом случае любая компонента
вектора
приоритета
V
удовлетворяет соотношению:
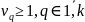 .
.
С). Весовой вектор = ) представляет собой k-мерный вектор, компоненты которого связаны соотношениями:
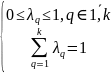 (21)
(21)
Компонента
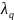 вектора
имеет смысл весового
коэффициента,
определяющего относительное превосходство
q-го
критерия над остальными.
вектора
имеет смысл весового
коэффициента,
определяющего относительное превосходство
q-го
критерия над остальными.
Пусть
локальные критерии упорядочены в смысле
ряда приоритета I.
Тогда соседние компоненты
и
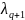 весового вектора
связаны соотношением:
весового вектора
связаны соотношением:
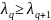 , и компоненты векторов V и
связаны соотношением:
, и компоненты векторов V и
связаны соотношением: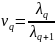 .
При
вычислении вектора
можно
воспользоваться следующим соотношением,
связывающим
компоненту
весового вектора
с компонентами вектора приоритета V:
.
При
вычислении вектора
можно
воспользоваться следующим соотношением,
связывающим
компоненту
весового вектора
с компонентами вектора приоритета V:
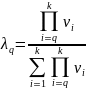 (22)
(22)
Достоинство принципа гибкого приоритета состоит в том, что диспропорции между необходимым, потенциально возможным и реально достижимым – рассматриваются как движущие силы для:
- развития инновационной деятельности и перевооружения отечественного производства на высокие технологии мирового уровня конкурентоспособности; - привлечения необходимых дополнительных ресурсов из внешнего мира.
