
- •Часть 3
- •Часть 3
- •Введение
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 27
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Приложения тройных интегралов
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 29
- •Примеры решения задач
- •Занятие 35-36 вычеты и их вычисление. Основная теорема о вычетах. Применние вычетов к вычислению интегралов
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Заключение
- •Библиографический список
- •Занятие № 29. Интегрирование функций комплексного
- •Часть 3
- •В авторской редакции
Занятие № 29
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ КОМПЛЕКСНГО
ПЕРЕМЕННОГО. ТЕОРЕМА КОШИ
И ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ
Литература: [2], с. 117-125; [8], с. 32-46; [9], с. 142-157.
Основные понятия
Пусть
на комплексной плоскости задана
ориентированная кусочно-гладкая кривая
 ,
на которой определена функция
,
на которой определена функция
 .
Разобьем эту кривую на
.
Разобьем эту кривую на
 частей
частей
Контрольные вопросы и задания
1. Дайте определение интеграла от функции комплексного переменного.
2. Как вычислить интеграл от функции комплексного переменного?
3. Сформулируйте теорему Коши для простого и сложного контура.
4. Как применяется интегральная формула Коши для вычисления интегралов по замкнутым контурам?
Примеры решения задач
Пример
1. Вычислить
 ,
где
,
где
 - отрезок прямой, соединяющей точки
- отрезок прямой, соединяющей точки
 и
и
 .
.
Решение.
Выделим действительную и мнимую часть
подынтегральной функции
 .
Для этого перепишем ее в виде
.
Для этого перепишем ее в виде
 .
Отсюда следует, что
.
Отсюда следует, что
 ,
,
 .
Применим формулу
.
Применим формулу

 .
Получаем, что вычисление
.
Получаем, что вычисление
 сводится к вычислению двух криволинейных
интегралов:
сводится к вычислению двух криволинейных
интегралов:
 .
Уравнение отрезка прямой, проходящей
через точки
и
,
будет
,
где
.
Уравнение отрезка прямой, проходящей
через точки
и
,
будет
,
где
 ,
а значит
,
а значит
 .
Поэтому
.
Поэтому

 .
.
Пример
2. Вычислить
 ,
где
- окружность единичного радиуса с центром
в точке
,
где
- окружность единичного радиуса с центром
в точке
 (обход против часовой стрелки,
- целое число).
(обход против часовой стрелки,
- целое число).
Решение.
Так как на окружности
 ,
то
,
то
 (
( )
и
)
и
 .
Тогда
.
Тогда


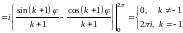 .
.
При
 результат вычислений согласуется с
теоремой Коши. При
результат вычислений согласуется с
теоремой Коши. При
 функция
функция
 не определена и не дифференцируема в
точке
.
Интеграл не равен нулю. При
не определена и не дифференцируема в
точке
.
Интеграл не равен нулю. При
 подынтегральная функция не определена
в точке
и теорема Коши также не применима, но
интеграл равен нулю.
подынтегральная функция не определена
в точке
и теорема Коши также не применима, но
интеграл равен нулю.
Пример
3. Вычислить
 ,
где
:
.
,
где
:
.
Решение. Аналогично примеру 2

 .
.
Пример
4. Вычислить
интеграл
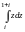 .
.
Решение.
Так как подынтегральная функция является
аналитической, то можно использовать
формулу Ньютона-Лейбница:
 .
.
Пример
5. Вычислить
 ,
где
- окружность: а)
,
где
- окружность: а)
 ,
б)
,
б)
 .
.
Решение.
а) Если
- окружность радиуса 2, то подынтегральная
функция
 является аналитической в каждой точке
круга
является аналитической в каждой точке
круга
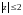 (рис. 2,а).
Поэтому, в силу теоремы Коши
(рис. 2,а).
Поэтому, в силу теоремы Коши
 .
.

а) б) в)
Рис. 2
б)
Если
- окружность радиуса 4, то точка
 (в ней функция не определена) принадлежит
кругу
(в ней функция не определена) принадлежит
кругу
 (рис. 2,б).
Представим подынтегральную функцию в
виде
(рис. 2,б).
Представим подынтегральную функцию в
виде
 ,
где
,
где
 является аналитической в каждой точке
круга
.
Применим интегральную формулу Коши (
является аналитической в каждой точке
круга
.
Применим интегральную формулу Коши ( )
)
 .
Получим
.
Получим
 .
.
Пример
6. Вычислить
 ,
где
:
,
где
:
 .
.
Решение.
Подынтегральная функция
 является аналитической в круге
является аналитической в круге
 всюду кроме точки
всюду кроме точки
 (рис. 2,в).
Выделим под знаком интеграла функцию
(рис. 2,в).
Выделим под знаком интеграла функцию
 ,
являющуюся аналитической в круге
.
Воспользуемся интегральной формулой
Коши для производной
,
являющуюся аналитической в круге
.
Воспользуемся интегральной формулой
Коши для производной

 .
При
и
.
При
и
 получим
получим
 .
.
Задачи и упражнения для самостоятельного решения
Вычислить интегралы:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
Вычислить интегралы:
а)
 ,
где
,
где
 ;
;
б)
 ,
где
,
где
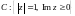 ;
;
в)
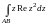 ,
где
,
где
 -
отрезок прямой,
-
отрезок прямой,
 ,
,
 .
.
Вычислить с помощью интегральной формулы Коши следующие интегралы:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)
 ;
д)
;
д)
 .
.
Форма отчетности: устный опрос, типовой расчет, коллоквиум.
Занятие 30-34
РАЗЛОЖЕНИЕ ФУНКЦИЙ КОМПЛЕКСНОГО
ПЕРЕМЕННОГО В РЯДЫ ТЕЙЛОРА И ЛОРАНА.
ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ
И ИХ КЛАССИФИКАЦИЯ
 ,
с. 125-132;
,
с. 125-132;
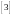 ,
с. 46-70;
,
с. 46-70;
 ,
с. 160-172.
,
с. 160-172.
Контрольные вопросы и задания
Запишите ряд Тейлора для функции комплексного переменного , аналитической в круге
 .
Как определяются его коэффициенты?
.
Как определяются его коэффициенты?Сформулировать теорему Тейлора. Каковы условия разложимости функции в ряд Тейлора?
Записать разложения в ряд Тейлора для основных элементарных функций:
 ,
,
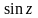 ,
,
 ,
,
 ,
,
 ,
,

Дать определение ряда Лорана функции . Как определяются его коэффициенты?
Сформулировать теорему Лорана. Каковы условия сходимости ряда Лорана? Какова его область сходимости?
Какие ряды называются правильной и главной частями ряда Лорана?
Какая точка называется особой точкой функции? В каком случае она называется изолированной особой точкой?
Какая особая точка называется:
а) устранимой; б) полюсом; в) существенно особой?
Как зависит вид ряда Лорана от характера особой точки?
Как связаны полюсы функции
 с нулями функции
?
Что такое кратность полюса?
с нулями функции
?
Что такое кратность полюса?
