
- •Министерство образования и науки российской федерации
- •Введение
- •Общие рекомендации
- •Вопросы программы для контрольной работы № 3
- •Раздел I. Неопределенные интегралы
- •Тема 1. Неопределенные интегралы
- •Раздел II. Определенный интеграл
- •Тема 2. Определенный интеграл
- •Вопросы программы для контрольной работы № 4
- •Раздел V. Вектор – функция скалярного аргумента
- •Тема 5. Вектор-функция скалярного аргумента
- •Раздел VI. Двойные интегралы
- •Тема 6. Двойные интегралы
- •Раздел VII. Криволинейные интегралы
- •Тема 7. Криволинейные интегралы
- •Определение варианта
- •Контрольная работа № 3
- •Контрольная работа № 4
- •3 94006 Воронеж, ул. 20-летия Октября, 84
Раздел V. Вектор – функция скалярного аргумента
Тема 5. Вектор-функция скалярного аргумента
1. Определение вектор-функции скалярного аргумента. Годограф.
2. Задание вектор-функции с помощью координат. Параметрическое задание линии (годографа).
3. Определение производной вектор-функции. Ее геометрический и механический смысл.
4. Дифференциал вектор-функции. Дифференциал длины годографа.
5. Дифференциал длины кривой, заданной параметрически.
6. Уравнения нормальной плоскости, проведенной через точку годографа.
7. Уравнения касательной, проведенной через точку годографа.
8. Вторая производная вектор-функции и ее механический смысл.
9. Средняя кривизна и кривизна линии в ее точке. Формула для нахождения кривизны годографа в заданной точке.
Литература: [2, гл. VII, §5, задачи 1127 – 1131, 1134, 1135, 1138, 1141 – 1143, 1145, 1146]; [1, гл. IX].
Раздел VI. Двойные интегралы
Тема 6. Двойные интегралы
1. Определение двойного интеграла, его геометрический смысл.
2. Свойства двойного интеграла.
3. Вычисление двойного интеграла в декартовой системе координат.
4. Вычисление двойного интеграла в полярной системе координат.
5. Вычисление объемов и площадей плоских фигур.
6. Механические приложения двойного интеграла: вычисление массы,
статических моментов, моментов инерции, координат центра тяжести
плоской пластины.
Литература: [1, т. 2, глава XIV]; [3, гл. XII, §1-6]; [4]; [5, гл. XI, §53]; [6, с. 24-30].
Раздел VII. Криволинейные интегралы
Тема 7. Криволинейные интегралы
1. Определение и свойства криволинейного интеграла I рода (по дуге).
2. Формулы для вычисления криволинейного интеграла I рода.
3. Вычисление длины дуги.
4. Вычисление массы материальной дуги, ее моментов инерции, координат ее центра тяжести.
5. Определение и свойства криволинейного интеграла II рода (по коорди- натам).
6. Формулы для вычисления криволинейного интеграла II рода.
7. Вычисление площади плоской фигуры.
8. Вычисление работы переменной вектор-силы.
Литература: [1, т. 2, глава XV]; [3, гл. XIII]; [4]; [5, гл. XII, §55, §56]; [6, с. 31-33].
Определение варианта
Для определения номера своего варианта возьмите двузначное число, на которое оканчивается номер вашего шифра (номер вашей зачетной книжки). Если оно не превосходит 20, то это номер вашего варианта. В противном случае вычитайте из этого числа 20 до тех пор, пока остаток не станет меньше 21. Тогда этот остаток и есть номер вашего варианта.
Условие задачи состоит из общей для всех вариантов формулировки и двадцати вариантов конкретных данных. Именно для этих данных вам надлежит выполнить решение своего варианта. При оформлении контрольной работы условия задач следует переписывать полностью. Каждая контрольная работа выполняется в отдельной тетради с полями и сдается (отсылается) для проверки в установленное деканатом время (до начала сессии).
Контрольная работа № 3
Задача 1. Найти неопределенные интегралы. В пп. а) и б) результаты проверить дифференцированием.
1.
a)
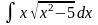 ; б)
; б)
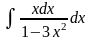 ; в)
; в)
 ;
;
г)
 ; д)
; д)
 е)
е)
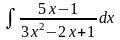 .
.
2.
а)
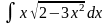 ; б)
; б)
 ; в)
; в)
 ;
;
г)
 ; д)
; д)
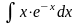 ;
е)
;
е)
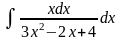 .
.
3.
а)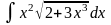 ; б)
; б)
 ;
в)
;
в)
 ;
;
г) ; д)
; д) ;
е)
;
е)
 .
.
4.
а) 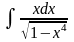 б)
б)
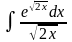 ; в)
; в)
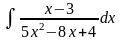 ;
;
г)
 ; д)
; д)
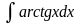 ; е)
; е)
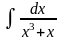 .
.
5.
а)
 ; б)
; б) ; в)
; в)
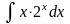 ;
;
г)
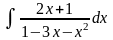 ; д)
; д)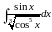 ; е)
; е)
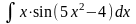 .
.
6.
а)
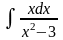 ; б)
; б)
 ; в)
; в) ;
;
г)
 ; д)
; д)
 ; е)
; е)
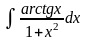 .
.
7.
а)
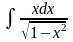 ; б)
; б)
 ; в)
; в)
 ;
;
г)
 ; д)
; д)
 ; е)
; е)
 .
.
8.
а)
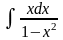 ; б)
; б)
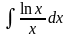 ; в)
; в)
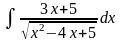 ;
;
г)
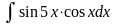 ; д)
; д)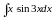 ; е)
; е)
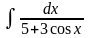 .
.
9.
а)
 ; б)
; б)
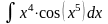 ; в)
; в)
 ;
;
г)
 ; д)
; д)
 ; е)
; е)
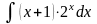 .
.
10.
а)
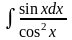 ; б)
; б)
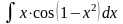 ; в)
; в)
 ;
;
г)
 ; д)
; д)
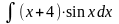 ;
е)
;
е)
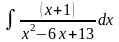 ;
;
11.
а)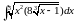 ; б)
; б)
 в)
в)
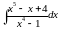 ;
;
г)
 ; д)
; д)
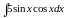 ;
е)
;
е)
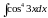 ;
;
12.
а)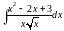 ; б)
; б)
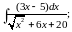 в)
в)
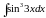 ;
;
г)
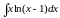 ; д)
; д)
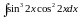 ; е)
; е)
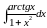 ;
;
13.
а)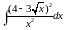 ; б)
; б)
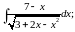 в)
в)
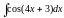 ;
;
г)
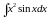 ; д)
; д)
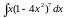 ;
е)
;
е)
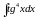 ;
;
14.
а)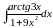 ; б)
; б)
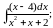 в)
в)
 ;
;
г)
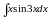 ;
д)
;
д)
 ;
е)
;
е)
 ;
;
15.
а) ; б)
; б)
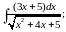 в)
в)
 ;
;
г)
 ; д)
; д)
 ;
е)
;
е)
 ;
;
16.
а)
; б)
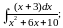 в)
в)
 ;
;
г)
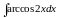 ; д)
; д)
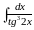 ; е)
; е)
 ;
;
17.
а) ; б)
; б)
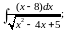 в)
в)
 ;
;
г)
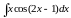 ; д)
; д)
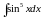 ;
е)
;
е)
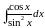 ;
;
18.
а)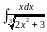 ; б)
; б)
 в)
в)
 ;
;
г)
 ; д)
; д)
 ;
е)
;
е)
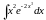 ;
;
19.
а) ; б)
; б)
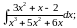 в)
в)
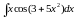 ;
;
г)
 ; д)
; д)
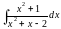 ;
е)
;
е)
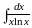 ;
;
20.
а)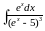 ; б)
; б)
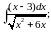 в)
в)
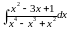 ;
;
г)
 ; д)
; д)
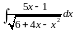 ;
е)
;
е)
 .
.
Задача 2. Вычислить определенные интегралы.
1.
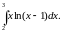 2.
2.
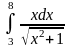 . 3.
. 3.
 .
.
4.
 .
5.
.
5.
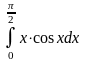 . 6.
. 6.
 .
.
7.
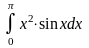 . 8.
. 8.
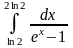 . 9.
. 9.
 .
.
10. . 11.
. 11.
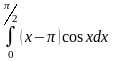 . 12.
. 12.
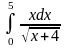 .
.
13.
 . 14.
. 14.
 . 15.
. 15.
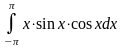 .
.
16.
 . 17.
. 17.
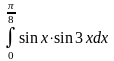 . 18.
. 18.
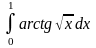 .
.
19.
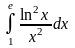 . 20.
. 20.
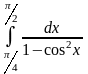 .
.
Задача 3. Вычислить несобственные интегралы или доказать их расходимость.
1.
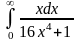 . 2.
. 2.
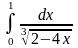 . 3.
. 3.
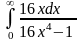 .
.
4.
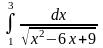 . 5.
. 5.
 . 6.
. 6.

 .
.
7.
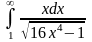 . 8.
. 8.
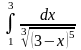 . 9.
. 9.
 .
.
10.
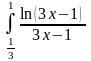 . 11.
. 11.
 . 12.
. 12.
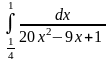 .
.
13.
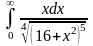 . 14.
. 14.
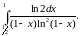 15.
15.
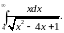
16.
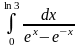 . 17.
. 17.
 . 18.
. 18.

19.
 . 20.
. 20.
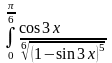 .
.
Задача 4. Используя определенный интеграл, вычислить:
1.
Площадь фигуры, ограниченной линиями:
 .
.
2.
Объем тела, полученного от вращения
вокруг оси OX
фигуры, ограниченной линиями
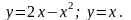
3.
Длину дуги линии
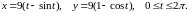
4.
Площадь фигуры, ограниченной линиями:
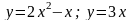 .
.
5.
Объем тела, полученного от вращения
вокруг оси OX
фигуры, ограниченной линиями

6.
Длину дуги линии
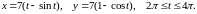
7.
Площадь фигуры, ограниченной линиями:
 .
.
8.
Объем тела, полученного от вращения
вокруг оси OX
фигуры, ограниченной линиями
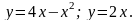
9.
Длину дуги линии
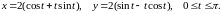 .
.
10.
Площадь фигуры, ограниченной линиями:
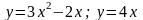 .
.
11.
Объем тела, полученного от вращения
вокруг оси OX
трапеции,
образованной прямыми
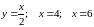 и осью OX.
и осью OX.
12.
Длину дуги линии

13.
Площадь фигуры, ограниченной осью OX
и линиями:
 .
.
14.
Площадь фигуры, ограниченной кривой
 ,
прямыми
,
прямыми
 и осью OY.
и осью OY.
15.
Объем тела, полученного от вращения
вокруг оси OY
фигуры,
ограниченной линиями
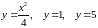 .
.
16.
Длину дуги линии
 .
.
17.
Площадь фигуры, ограниченной кривой:
 .
.
18.
Объем тела, полученного от вращения
вокруг оси OX
фигуры, ограниченной параболой
 и прямой
и прямой
 .
.
19.
Длину дуги линии
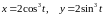 .
.
20.
Площадь фигуры, ограниченной кривой
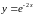 и прямыми
и прямыми
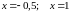 .
.
