ФГБОУВПО «Воронежский государственный

технический университет »

СПРАВОЧНИК МАГНИТНОГО ДИСКА

(Кафедра высшей математики и

физико-математического моделирования)

методические указания

к выполнению курсовой работы по дисциплине «Математика» для студентов специальностей 15.03.06 «Мехатроника и робототехника», 27.03.04 «Управление в технических системах» , 13.03.02 «Электроэнергетика и электротехника», 35.03.06 «Агроинженерия», очной формы обучения

Составители: А.А. Катрахова, В.С. Купцов, Е.М. Васильев

Курс .docx 358 Kбайт 14.03.2015 уч.-изд. 3.2 л.

(название файла) (объем файла) (дата) (объем издания

ФГБОУВПО «Воронежский государственный

технический университет »

(Кафедра «высшей математики и физико-математического моделирования») методические указания

к выполнению курсовой работы по дисциплине «Математика» для студентов специальностей 15.03.06 «Мехатроника и робототехника», 27.03.04 «Управление в технических системах» , 13.03.02 «Электроэнергетика и электротехника», 35.03.06 «Агроинженерия», очной формы обучения

Воронеж 2015

Составители: канд. физ.-мат. наук А.А. Катрахова, канд. физ.-мат. наук В.С. Купцов, канд. техн. наук Е.М. Васильев

УДК 517

Методические указания к выполнению курсовой работы по дисциплине «Математика» для студентов специальностей 15.03.06 «Мехатроника и робототехника», 27.03.04 «Управление в технических системах» , 13.03.02 «Электроэнергетика и электротехника», 35.03.06 «Агроинженерия», очной формы обучения / ФГБОУВПО Воронежский государственный технический университет»; cост. А.А. Катрахова, В.С. Купцов, Е.М. Васильев. Воронеж, 2015. 56 с.

Данные методические указания предназначены для студентов специальностей 15.03.06 «Мехатроника и робототехника», 27.03.04 «Управление в технических системах» , 13.03.02 «Электроэнергетика и электротехника», 35.03.06 «Агроинженерия», очной формы обучения. Методические указания содержит необходимые краткие теоретические сведения, разобранный пример, а также задание на курсовую работу.

Методические указания подготовлены на магнитном

носителе в текстовом редакторе MS Word и содержатся

в файле «Курс .docx »

Табл. 11. Ил. 12. Библиогр.: 10 назв.

Рецензент канд. физ.-мат. наук, доц. М.В. Юрьева

Ответственный за выпуск зав. кафедрой д-р физ.-мат.

наук, проф. И.Л. Батаронов

Издается по решению редакционно-издательского совета

Воронежского государственного технического университета

© ФГБОУВПО «Воронежский государственный

т

ехнический университет», 2015

Введение

Настоящие методические указания содержат необходимые краткие теоретические сведения, пример выполнения курсовой работы, а также задание на курсовую работу. В настоящих методических указаниях даются рекомендации по оформлению этой работы. Содержание методических указаний соответствует программе курса математики для студентов инженерно-технических специальностей вузов рассчитанной на 600 часов и утвержденной Министерством образования Российской Федерации в соответствии с образовательными стандартами

1. Курсовая работа Условный экстремум. Метод множителей Лагранжа

Теоретические сведения

Пусть требуется найти экстремум функции n переменных f(x₁,x₂,…,x_n) при условии, что переменные x₁,x₂,…,x_n связаны соотношениями (ограничениями)

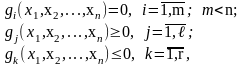
среди которых количество m ограничений-равенств меньше числа n переменных, а количество l и r ограничений-неравенств может быть произвольным.

Для нахождения значений {x₁,x₂,…,x_n}=Х, необходимо доставляющих экстремумы функции f(X), можно воспользоваться методом неопределенных множителей Лагранжа:

1. Ограничения-неравенства g(X)³0 приводятся к виду j(Х)£0, где j(Х) = - g(X).

2. Полученные ограничения-неравенства

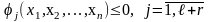
в свою очередь приводятся к ограничениям-равенствам путем введения l+r дополнительных переменных

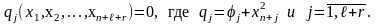
В результате задача поиска условного экстремума примет канонический вид:

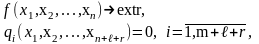
в котором соотношение m+l+r < n+l+r указывает на возможность получения множества допустимых решений, а значит, и нахождения среди них тех, которые доставляют экстремум f(X).

3. Составляется функция Лагранжа:

Ф(x₁,…,x_n,l₁,…,l_m+l+r) = f(x₁,x₂,…,x_n)+l₁q₁+l₂q₂+…+l_m+l+rq_m+l+r ,

в которой дополнительные переменные {l₁,…,l_m+l+r}=L называются неопределенными множителями Лагранжа.

Для составленной функции Лагранжа можно ставить задачу нахождения безусловного экстремума

Ф(Х,L) ® extr,

результат решения которой будет совпадать с искомым решением исходной задачи нахождения условного экстремума.

4. Для функции Ф(Х,L) составляются необходимые условия существования экстремума:

ÑФ(Х,L)=0

Или

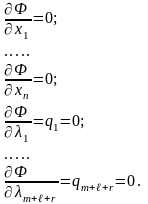
5. Полученную систему уравнений ÑФ(Х,L)=0 решают, и в результате решения находят значения

,

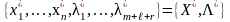удовлетворяющие необходимым условиям существования экстремума.

6. Для решения вопроса о том, существует ли в найденных точках максимумы или минимумы следует воспользоваться достаточными условиями существования экстремумов, которые для гладких функций Ф(×) формулируются следующим образом:

если в некоторой точке матрица вторых производных 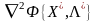положительно определена, то в анализируемой точке лежит минимум функции f(Х);

если отрицательно определена - максимум.

Если Ф(Х,L) негладкая, то можно использовать достаточные условия вида, например, для максимума:

Ф(Х,L*) £ Ф(Х*,L*) = Ф(Х*,L),

однако проверка этих условий при большом числе переменных трудоемко, и при решении практических задач вопрос о наличии минимума или максимума решается на основании дополнительных соображений, вытекающих из содержания задачи.

Пример задания.

Найти состав продуктов наименьшей стоимости, обеспечивающий недельную потребность человека в белках, жирах и углеводах.

Числовые данные к задаче представлены в таблице 1.

Таблица 1

Продукт	Содержание белков, о.е.	Содержание жиров, о.е.	Содержание углеводов, отн. единиц	Цена за1 кг
Хлеб	0,07	0,01	0,5	10
Масло	0,06	0,8	0,09	60
Недельная потребность, кг	0,6	0,7	2,5

Решение. Обозначим через х₁ и х₂ массы хлеба и масла, составляющие искомый состав продуктов. В качестве целевой функции f(x₁,x₂) возьмем суммарную стоимость продуктов: f(x₁,x₂) = 10х₁ + 60х₂. Недельную потребность в белках, жирах и углеводах примем за ограничения, накладываемые на переменные х₁ и х₂.

В указанной постановке решаемая задача может быть сформулирована как задача поиска условного экстремума:

10х₁ + 60х₂ ® min; 0,07х₁ + 0,06х₂ ³ 0,6;

0,01х₁ + 0,8х₂ ³ 0,7; 0,5х₁ + 0,09х₂ ³ 2,5; х₁³0; х₂³0.

Решим задачу методом множителей Лагранжа.

1. Приведем ограничения к виду j(Х) £ 0:

0,6 - 0,07х₁ - 0,06х₂ £ 0; 0,7 - 0,01х₁ - 0,8х₂ £ 0;

2,5 - 0,5х₁ - 0,09х₂ £ 0; -х₁£0; -х₂£0.

2. Путем ведения дополнительных переменных х₃,х₄,х₅,х₆,х₇ перейдем к ограничениям-равенствам:

0,6 - 0,07х₁ - 0,06х₂ + х₃² = 0; 0,7 - 0,01х₁ - 0,8х₂ +х₄² = 0;

2,5 - 0,5х₁ - 0,09х₂ +х₅² = 0; -х₁ + х₆² = 0; -х₂ + х₇² = 0.

3. Сформируем функцию Лагранжа:

Ф(х₁,х₂,х₃,х₄,х₅,х₆,х₇,l₁,l₂,l₃,l₄,l₅) =

= 10х₁ + 60х₂ +l₁(0,6 - 0,07х₁ - 0,06х₂ + х₃²) +

+l₂(0,7 - 0,01х₁ - 0,8х₂ +х₄²)+l₃(2,5 - 0,5х₁ - 0,09х₂ +х₅²)+

+l₄(-х₁ + х₆²)+ l₅(-х₂ + х₇²).

4. Составим необходимые условия ÑФ(Х,L)=0:

5. Решить полученную систему нелинейных уравнений можно каким-либо формальным методом с помощью, например, средств математического пакета Mathcad:

В результате использования приведенной программы с различными начальными условиями было получено четыре решения:

х₁ = 70; х₂ = 0; f₁(х₁,х₂) = 700;

х₁ = 7,906; х₂ = 0,776; f₂(х₁,х₂) = 125,63;

х₁ = 4,051; х₂ = 5,274; f₃(х₁,х₂) = 356,96;

х₁ = 0; х₂ = 27,778; f₄(х₁,х₂) = 1666,68.

Лучшим решением из приведенного перечня является второе.

Необходимо отметить, что значительный размер сформированной системы уравнений, полученных из необходимых условий (12 уравнений), вызван:

во-первых, тем, что переход от ограничений-неравенств к ограничениям-равенствам осуществляется путем введения дополнительных переменных х₃,х₄,х₅,х₆,х₇, число которых равно числу ограничений-неравенств;

во-вторых, тем, что переход от задачи нахождения условного экстремума к задаче безусловного поиска возможен, в соответствии с методом Лагранжа, с помощью введения дополнительных переменных l₁,l₂,l₃,l₄,l₅, число которых равно общему числу ограничений задачи.

Таким образом, решение задачи методом Лагранжа получено ценой повышения ее размерности. Этот недостаток ограничивает область применения метода Лагранжа сравнительно простыми задачами, поэтому с повышением числа переменных и ограничений целесообразно переходить к численным методам математического программирования.

Анализ решения.

Для проверки правильности полученных результатов и осмысления содержательной стороны решаемой задачи поиска условного экстремума проведем ее анализ. Переписав исходную систему ограничений-неравенств в виде

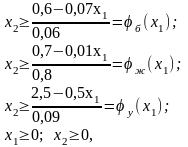
получаем возможность графически представить эти ограничения на плоскости х₂ох₁ в виде прямых j_б(х₁); j_ж(х₁); j_у(х₁); х₂=0; х₁=0, снабдив их штриховкой, направленной в сторону области допустимых значений х₁ и х₂, рис. 2.1,2,2.

Как следует из рис. 1, область допустимых решений не является замкнутой, допустимые значений х₁ и х₂ не ограничены сверху и любая пара их допустимых значений, например, точка D, обеспечивает необходимую потребность в белках, жирах и углеводах с избытком.

Поскольку целью задачи является нахождение минимума затрат, пропорциональных массам х₁ и х₂, очевидно, что искомое решение будет лежать на границе области допустимых решений, составленной отрезками 1-2-3-4, ограничивающей значения х₁ и х₂ снизу.

При этом решения на интервале [1-2) обеспечивают точное выполнение потребности в жирах (0,7кг) и избыток белков и углеводов;

на интервале (2-3) - точное обеспечение потребности в белках (0,6кг) и избыток жиров и углеводов;

на интервале (3-4] - точное обеспечение потребности в углеводах (2,5кг) при избытке белков и жиров.

В смежных точках 2 и 3 активно по два ограничения:

в точке 2 - строгое выполнение условия по белкам и жирам при избытке углеводов;

в точке 3 - строгое выполнение условий по белкам и углеводам при избытке жиров.

Чтобы ответить на вопрос, в какой же точке ломаной 1-2-3-4 расположен минимум функции f(x₁,x₂) =10x₁+60x₂, построим проекции линий равного уровня f(x₁,x₂) = 20, f₂(x₁,x₂)=125,63 и f₃(x₁,x₂)=356,96 на плоскость х₂ох₁, т.е. построим в этой плоскости прямые

10x₁+60x₂=20; 10x₁+60x₂=125,63 ; 10x₁+60x₂=356,96,

две из которых, как и следовало ожидать из результатов аналитического решения, проходят через точки 2 и 3, рис. 2.

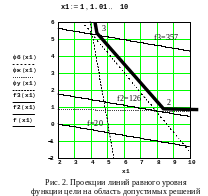
Взаимное расположение построенных линий f(x₁,x₂), f₂(x₁,x₂), f₃(x₁,x₂) и границы 1-2-3-4 показывает, что всякая линия уровня со значением f(x₁,x₂)<126 располагается ниже прямой f₂(x₁,x₂) и, следовательно, не будет иметь общих точек с границей 1-2-3-4, т.е. решение задачи со значением f(x₁,x₂), меньшим, чем f₂(x₁,x₂), не существует, и в точке 2 находится искомый условный минимум.

Найденное решение, как это было установлено выше, обеспечивает избыток углеводов, но, тем не менее, это лучшее решение при данных условиях. Если провести линию уровня через любую другую точку ломаной 1-2-3-4, то можно убедиться, что она будет соответствовать значению f(x₁,x₂)>126, т.е. в точке 2 располагается единственный условный минимум задачи.

Неактивность в окрестностях экстремума ограничений х₁³0, x₂³0 свидетельствует о том, что эти условия при составлении функции Лагранжа можно было исключить и значительно понизить размерность задачи.

Кроме того, проведенный анализ показывает, что экстремум в данной задаче можно было найти более рациональным способом - решить систему двух уравнений, составляющих ограничения по белкам и жирам:

0,07х₁ + 0,06х₂ = 0,6; 0,01х₁ + 0,8х₂ = 0,7.

Р ешение этой системы и поверка граничных условий представлены в программе:

П роверка показывает полное совпадение результатов решением по методу Лагранжа, а также подтверждает ожидаемое строгое выполнение условий по белкам (0,6 кг) и жирам (0,7 кг) с избытком углеводов (4,652 > 2,5 кг).

Оформление титульного листа.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(ФБГОУ ВПО «ВГТУ»)

Кафедра высшей математики и физико-математического моделирования

Курсовая работа

по дисциплине «Математика»

Тема:

Вариант

Выполнил студент группы _________

Руководитель доцент каф. ВМФММ ________.

Защищена _________ ___________

дата оценка

Воронеж 2015