Типы конечных элементов

Наиболее очевидная классификация элементов предусматривает деление их на одномерные, двумерные и трехмерные. Эти группы могут разделяться в зависимости от того, включают ли узловые перемещения только значения функций (лагранжевы элементы) или также и значения производных (эрмитовы элементы).

Элементы, чаще всего используемые на практике, представлены ниже.

Ферменный элемент – прямолинейный стержень, который присоединяется к другим конструктивным элементам посредством идеальных шарниров (рис. 6). Если к нему не приложены поперечные нагрузки, то он будет испытывать лишь растяжение или сжатие. В каждом узле этого элемента рассматривается по три линейных степени свободы (на рис. 6 они показаны стрелками).

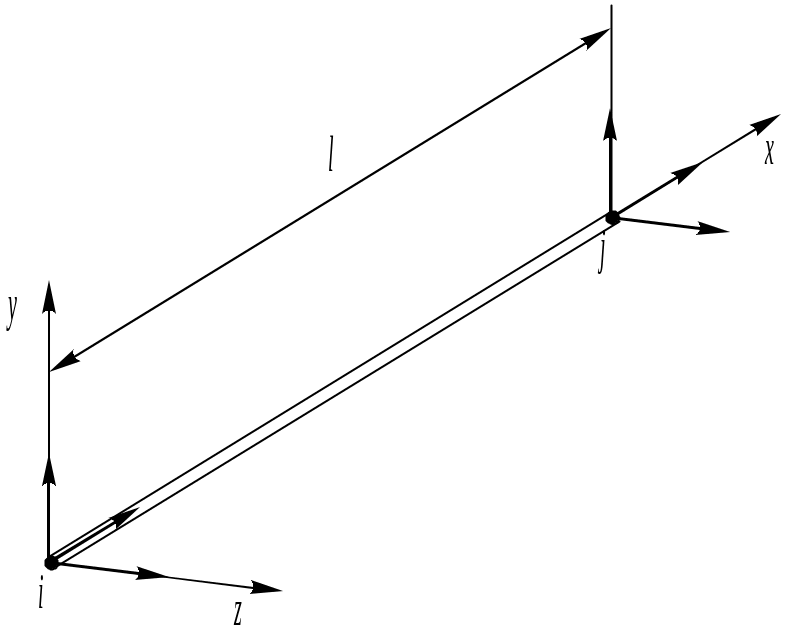
Рис. 6. Ферменный конечный элемент

Прямолинейный брус воспринимает в общем случае все виды нагрузок (растяжение, изгиб в двух плоскостях и кручение). Каждый узел такого элемента (рис. 7) имеет три линейных и три угловых степеней свободы.

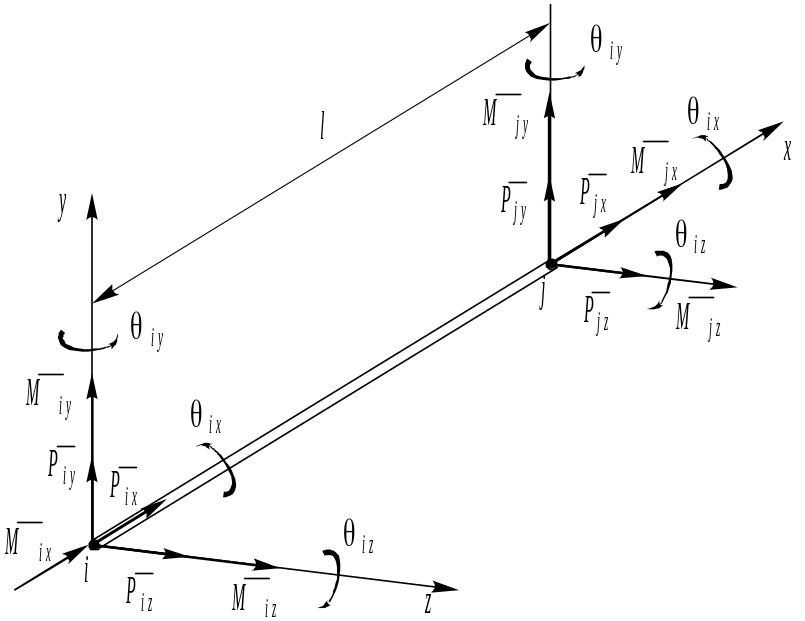
Рис. 7. Конечный элемент бруса

Эти элементы моделируют ферменные и пространственные рамные конструкции. В совокупности с пластинчатыми элементами стержневой элемент с шестимерными узлами позволяет моделировать подкрепленные элементы конструкций.

При исследовании плоского напряженного состояния могут быть использованы плоские конечные элементы треугольной и четырехугольной формы (рис. 8).

Рис. 8. Плоские конечные элементы

Узлы этих элементов расположены в углах и имеют по два линейных перемещения вдоль осей в своей плоскости.

Наиболее распространенными формами трехмерных элементов являются тетраэдр и параллелепипед (рис. 9).

Эти элементы играют важную роль при моделировании массивных пространственных конструкций и задач механики грунтов, их узлы размещены в вершинах и обладают тремя линейными степенями свободы.

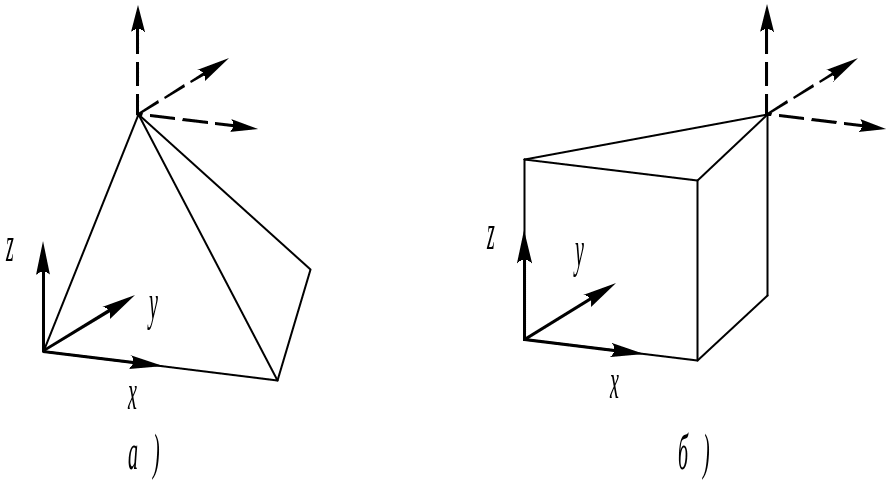
Рис. 9. Объемные конечные элементы

Пространственные тонкостенные конструкции наиболее просто аппроксимируются пластинчатыми элементами, испытывающими суперпозицию изгибного и мембранного напряженных состояний (рис. 10). Каждый узел таких элементов наделен шестью «инженерными» степенями свободы: тремя линейными перемещениями вдоль осей локальной системы отсчета и тремя углами поворотов вокруг этих осей.

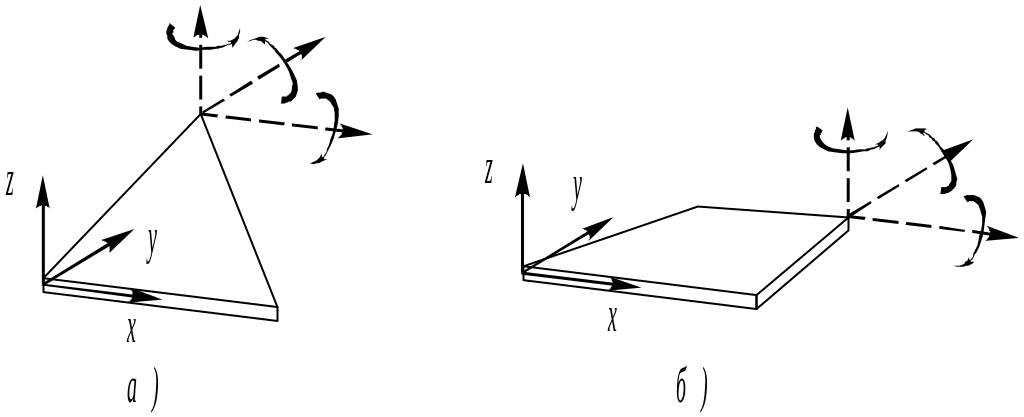
Рис. 10. Пластинчатые элементы

Вследствие своей простоты эти элементы позволяют с достаточной для инженеров точностью аппроксимировать и оболочечные конструкции.

Одной из важных областей применения МКЭ является расчет осесимметричных тел (рис. 11). При моделировании используется осесимметричный конечный элемент.

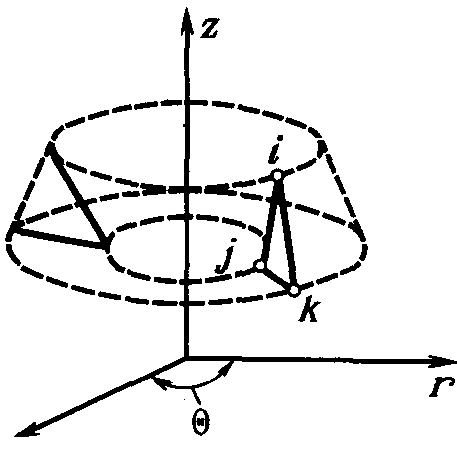
Рис. 11. Осесимметричный конечный элемент

Большое количество прикладных задач относится к этой области: расчет бетонных и стальных резервуаров, сосудов высокого давления, роторов и валов двигателей. Нагрузки также обычно бывают осесимметричными.

Прямой метод жесткости

Уравнение жесткости для элемента записывается в виде линейных алгебраических уравнений:

где [k] – матрица жесткости элемента, {F} – вектор сил и – вектор смещений для элемента.

Отдельный элемент матрицы [k] называется коэффициентом жесткости элемента и его физический смысл может быть определен из следующего условия: если перемещение полагается равным единице, а перемещения, отвечающие остальным степеням свободы, полагаются равными нулю , значение силы равно .

Соотношения между всеми силами и перемещениями для элемента с n степенями свободы имеет вид:

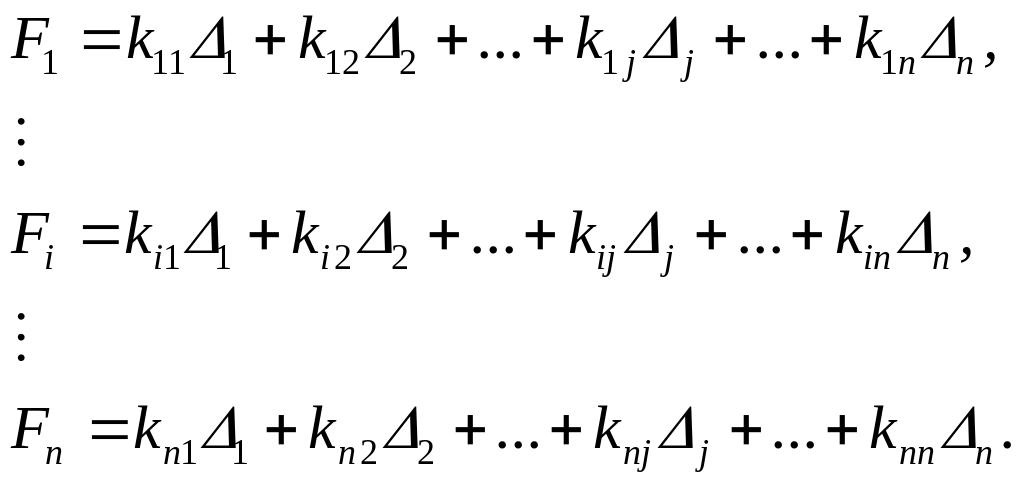
Степени свободы отвечают глобальной системе отсчета. Если соотношения между силами и перемещениями в каждом элементе определены численно, то применение прямого метода жесткости заключается в объединении приведенных соотношений в алгебраическом виде, как требуют условия равновесия и совместности в узлах сопряженных элементов. Это приводит к системе уравнений, связывающих силы и перемещения в узловых точках для ансамбля конечных элементов.

Для иллюстрации этой методики, поясняющей процесс формирования глобальной матрицы жесткости конструкции, выведем уравнения связи между силами и перемещениями в точке q по направлению оси x для конечно-элементной модели рис. 12.

Величины, отвечающие направлению x в узле q обозначим нижним индексом i. Все элементы лежат в плоскости x0y.

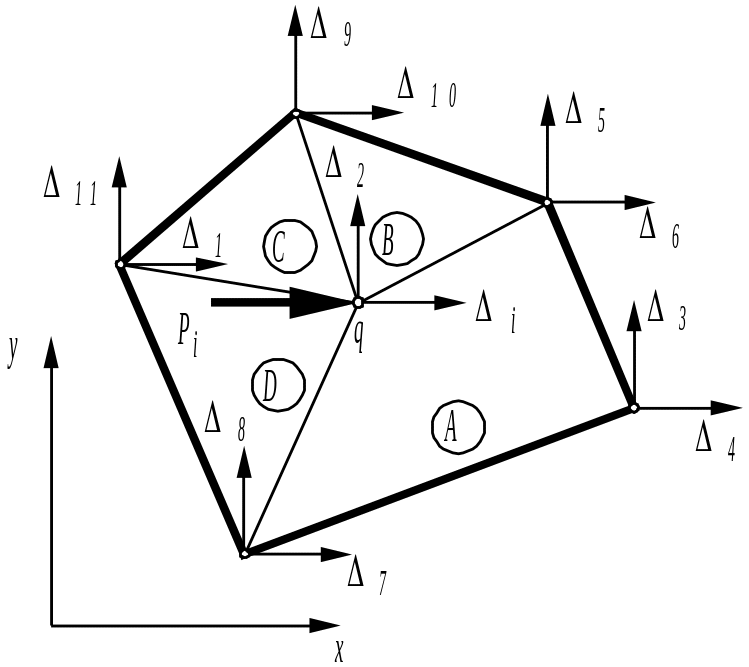
Рис. 12. Типичный узел плоской модели

Согласно условиям равновесия в узле, приложенная нагрузка равна сумме внутренних сил, действующих в соответствующих элементах, прилежащих к узлу. Для пояснения этого на рис. 13 показаны элементы, прилежащие к рассматриваемому узлу.

Из условия равновесия в направлении x:

где – внутренняя сила, действующая в направлении x в элементе A.

Подставляя в последнее уравнение выражения для внутренних сил , записанных в терминах соответствующих степеней свободы элемента получим:

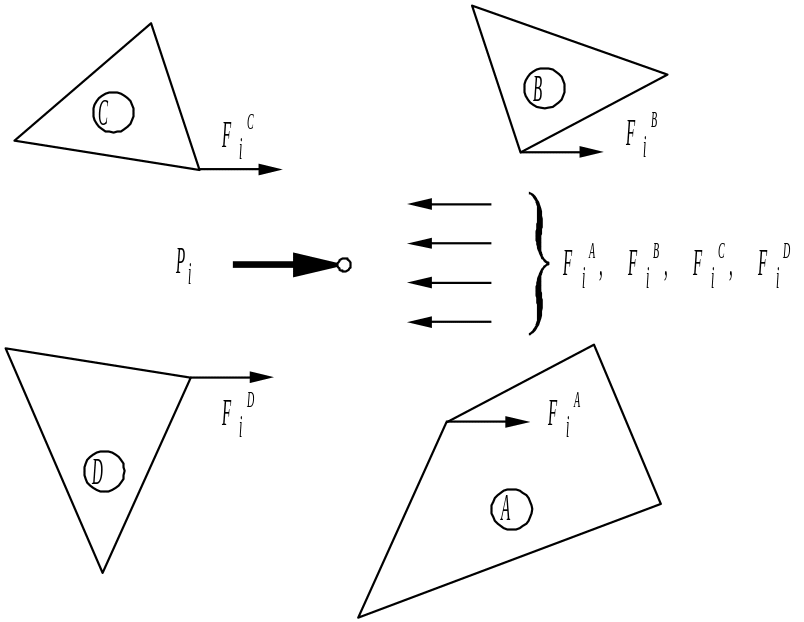
Рис. 13. Анализ равновесия в направлении

В силу совместности смещения для всех элементов одинаковы, поэтому

или

Рис. 14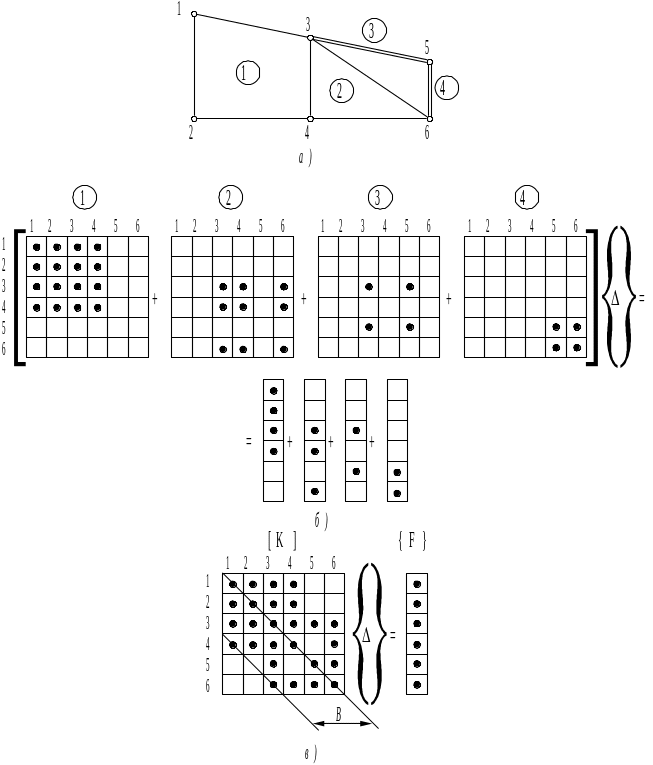

Здесь прописными буквами обозначены глобальные коэффициенты матрицы жесткости ансамбля конечных элементов.

Схема формирования глобальной матрицы жесткости и вектора узловой нагрузки исследуемой конструкции может быть рассмотрена на следующем примере. На рис. 14, а изображена модель, состоящая из четырех взаимосвязанных элементов.

Для каждого элемента строится локальная матрица жесткости, размерность которой соответствует числу его узловых степеней свободы. Коэффициенты матрицы жесткости размещаются в соответствии с матрицей связи, которая указывает номера узлов элемента при глобальной нумерации. На рис. 14, б показана схема формирования коэффициентов матриц жесткости конструкции и вектора узловой нагрузки. Полуширина ленты B глобальной матрицы жесткости для данного примера равна 4, если в каждом узле рассматривается одна степень свободы (рис. 14, в).