
- •Методические указания
- •Предисловие
- •Электромагнетизм
- •1. Основные формулы
- •2. Примеры решения задач
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •3. Задачи для самостоятельного решения Поле прямого тока
- •Поле кривого тока
- •Закон полного тока. Магнитный поток. Магнитные цепи.
- •Работа по перемещению проводника с током в магнитном поле. Электромагнитная индукция. Индуктивность
- •Контрольные задания по электромагнетизму
- •Библиографический список
- •Содержание
- •Методические указания
- •394026 Воронеж, Московский просп., 14
Решение:
Напряженность магнитного поля на бесконечно длинного цилиндра равна
![]() (1),
(1),
где n- число витков на единице длины,
k-число
слоев. Число витков
![]() в одном
в одном
слое намотки определится из формулы
![]() (2).
(2).
Тогда
![]() (3).
(3).
Подставляя
(3) в (1) и выражая из (1)
![]() ,
получим
,
получим
![]() ,
откуда
,
откуда
![]() (слоя)
(слоя)
Ответ: k=4
З адача
2.9. Вычислить
циркуляцию вектора магнитной индукции
вдоль контура, охватывающего токи
=10A,
=10A
, текущие в одном направлении, и ток
адача
2.9. Вычислить
циркуляцию вектора магнитной индукции
вдоль контура, охватывающего токи
=10A,
=10A
, текущие в одном направлении, и ток
![]() =20A,
текущий в противоположном направлении.
=20A,
текущий в противоположном направлении.
Д ано:
Решение
ано:
Решение
I1=10A По теореме о циркуляции
I2=15A вектора магнитной индукции
I3=20A вдоль произвольного контура L
I
L![]() I2
I2![]() I3
запишем
I3
запишем
Рис. 2.8![]()

![]()
![]() =
=![]()
![]()
Ответ:
Задача 2.10. Провод в виде тонкого полукольца радиусом R = 10 см находится в однородном магнитном поле (В = 50 мТл). По проводу течет ток = 10 А. Найти силу , действующую на провод, если плоскость полукольца перпендикулярна линиям магнитной индукции, а подводящие провода находятся вне поля.
Д ано:
Решение:
ано:
Решение:
R = 10 см=0,1м Расположим провод в плоскости чертежа
В
=
50мТл=![]()
![]() перпендикулярно
линиям магнитной
перпендикулярно
линиям магнитной
I = 10 А индукции (рис. 2.9) и выделим на нем
F -?
малый элемент
с током.
-?
малый элемент
с током.
Н а
этот элемент тока
а
этот элемент тока
![]() будет действовать
будет действовать
п
Рис. 2.9![]() .
Направление этой силы можно определить
по правилу векторного произведения или
по правилу левой руки.
.
Направление этой силы можно определить
по правилу векторного произведения или
по правилу левой руки.
Используя
симметрию, выберем координатные оси
так, как это изображено на рис.2.9, силу
представим в виде
![]()
где
![]() -единичные
векторы (орты);
-единичные
векторы (орты);
![]() и
и
![]() -проекции
вектора
на координатные оси Ох и Оу.
-проекции
вектора
на координатные оси Ох и Оу.
Силу , действующую на весь провод, найдем интегрированием:
![]() ,
,
где символ L указывает на то, что интегрирование ведется по всей длине провода L.
Из
соображений симметрии первый
интеграл равен нулю
![]() Тогда
Тогда
![]() (1)
(1)
Из
рис. 2.9 следует, что dFy
= dF![]() ,
где
dF
—
модуль вектора
,
где
dF
—
модуль вектора
![]() .
Так
как вектор
перпендикулярен
вектору
.
Так
как вектор
перпендикулярен
вектору
![]() ,
то dF
= IBdl.
Выразив
длину дуги dl
через
радиус R
и
угол
,
получим
,
то dF
= IBdl.
Выразив
длину дуги dl
через
радиус R
и
угол
,
получим ![]()
Тогда
![]() .
.
Введем
под
интеграл соотношения (1) и проинтегрируем
в пределах от
![]() до +
до +![]() (как это следует из рис 2.9):
(как это следует из рис 2.9):
![]()
Из
полученного выражения видно, что сила
сонаправлена
с положительным направлением оси Оу
(единичным
вектором
![]() ).
Найдем
модуль силы
:
).
Найдем
модуль силы
:
![]()
Произведем вычисления:
![]() (Н)
(Н)
Ответ: F=0,1 Н.
Дано: v
=
2
В
=
30мТл=
|
R-?, h-? |
Решение:
Рис. 2.10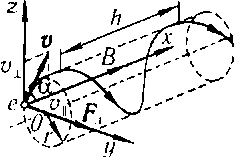 Р
Р![]() ,
направленную
перпендикулярно
к полю,
т.е.
вектору
и
,
направленную
перпендикулярно
к полю,
т.е.
вектору
и
![]() ,
,
направленную вдоль поля (рис. 2.10).
Проекция траектории электрона на плоскость, перпендикулярную к индукции , представляет собой окружность, радиус которой равен искомому радиусу винтовой траектории.
Из
рисунка
![]() ,
,
![]()
В
результате одновременного участия в
движениях по окружности со скоростью
![]() и прямой со скоростью
и прямой со скоростью
![]() электрон будет двигаться по винтовой
линии.
электрон будет двигаться по винтовой
линии.
Сила
Лоренца
![]() сообщает
электрону нормальное ускорение
сообщает
электрону нормальное ускорение
![]() .
По второму закону Ньютона,
.
По второму закону Ньютона,
![]() где
где
![]() .
Тогда
.
Тогда
![]()
откуда
![]()
где
![]() кг - масса электрона,
кг - масса электрона,
![]() Кл-заряд электрона
Кл-заряд электрона
Подставив значения величин, m, e, B и и произведя вычисления, получим
![]()
Шаг винтовой линии равен пути, пройденному электроном вдоль поля со скоростью за время, которое понадобится электрону для того, чтобы совершить один оборот,
h
=
![]()
где
![]() —
период вращения электрона. Тогда:
—
период вращения электрона. Тогда:
![]()
Поставив в эту формулу значения величин и вычислив, получим:
![]()
Ответ: R=0,19мм, h=2,06мм
Задача 2.12. Альфа-частица прошла ускоряющую разность потенциалов U = 104 В и влетела в скрещенные под прямым углом электрическое (Е = 10 кВ/м) и магнитное (В=0,1 Тл) поля. Найти отношение заряда альфа-частицы к ее массе, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории.
Дано: Решение
U = 104В Для того чтобы найти отношение
E=10кВ/м=![]() В/м
заряда
альфа-частицы
к ее массе
В/м
заряда
альфа-частицы
к ее массе
![]()
 воспользуемся
связью между
воспользуемся
связью между
![]() работой
сил
работой
сил
![]()
 ?
электрического
?
электрического
поля и изменением кинетической энергии частиц:
![]()
о
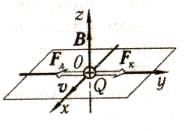
Рис. 2.11![]() (1)
(1)
Скорость альфа-частицы найдем из следующих соображений. В скрещенных электрическом и магнитном полях на движущуюся заряженную частицу действуют две силы:
а)
сила Лоренца
![]() ,
направленная
перпендикулярно скорости
и
вектору магнитной индукции
;
,
направленная
перпендикулярно скорости
и
вектору магнитной индукции
;
б)
кулоновская сила
![]() ,
сонаправленная
с вектором
электрического
поля (q
> 0).
,
сонаправленная
с вектором
электрического
поля (q
> 0).
Направим
вектор магнитной индукции
вдоль
оси
![]() (рис.
2.11), скорость
-
в положительном направлении оси
(рис.
2.11), скорость
-
в положительном направлении оси
![]() ,
тогда
,
тогда
![]() и
будут направлены так, как это указано
на рис. 2.11
и
будут направлены так, как это указано
на рис. 2.11
Альфа-частица,
не будет испытывать отклонения, если
геометрическая сумма сил
+
![]() будет равна нулю. В проекции на ось
будет равна нулю. В проекции на ось
![]() получим
следующее равенство (при этом учтено,
что вектор скорости
перпендикулярен
вектору магнитной индукции
и
получим
следующее равенство (при этом учтено,
что вектор скорости
перпендикулярен
вектору магнитной индукции
и
![]() :
:
![]()
откуда
![]()
Подставив это выражение скорости в формулу (1), получим
![]() (2)
(2)
Подставим значения E,U и В в (2) и вычислим:
![]()
Ответ: q/m=48,1 МКл/кг
Задача
2.13. Виток,
по которому течет ток I=20А,
свободно установится в однородном
магнитном поле В=16 мТл. Диаметр d
витка равен 10 см. Какую работу нужно
совершить , чтобы медленно повернуть
виток на угол
![]() относительно оси, совпадающей с диаметром?
относительно оси, совпадающей с диаметром?
Дано: I=20A В=16
мТл=16·10 D=10см=0,1м
|
А-? |
П
Рис. 2.12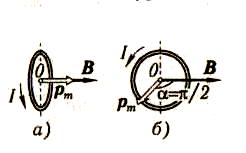
Работа сил поля в этом случае определяется выражением:
А=I(Ф2-Ф1) (1)
где Ф1 и Ф2 – магнитные потоки, пронизывающие контур в начальном и конечном положениях. Работа внешних сил будет равна модулю работе сил поля и противоположна её по знаку, т.е
![]()
![]() ,
(2)
,
(2)
В
начальный момент вектор магнитного
момента
![]() контура со направлен с вектором
контура со направлен с вектором
![]() (рис2.12(а))
и магнитный поток
(рис2.12(а))
и магнитный поток
![]() максимален(α=0, cosα=1),
т.е
=BS,
где S-
площадь контура . В конечном положении(
рис 2.12(б)) вектор
максимален(α=0, cosα=1),
т.е
=BS,
где S-
площадь контура . В конечном положении(
рис 2.12(б)) вектор
![]() перпендикулярен вектору В(α=
перпендикулярен вектору В(α=![]() и магнитный поток Ф2=0 .
и магнитный поток Ф2=0 .
Тогда выражение (2) примет вид:
![]() ,
где S=
,
где S=![]()
![]()
![]()
Подставим числовые значения, вычислим
![]() мДж
мДж
Ответ:
![]() 2,5
мДж
2,5
мДж
Задача
2.14. Прямой
бесконечный ток
=5A
и прямоугольная рамка с током
=3A
расположены в одной плоскости так, что
сторона рамки l=1м
параллельна прямому току и отстоит от
него на расстоянии r=0,1b,
где b
- длина другой стороны рамки (рис 2.13).
Определить какую работу необходимо
совершить для того, чтобы повернуть
рамку на угол α=90˚ относительно оси
![]() ,
параллельной прямому току и проходящей
через середины противоположных сторон
рамки b.
,
параллельной прямому току и проходящей
через середины противоположных сторон
рамки b.
Дано: =5A =3A l=1м; =0,1b;α=90˚ |
A-? |
Легко
видеть, что во втором положении магнитный
поток через рамку равен нулю:![]() =0.
=0.
Таким образом, необходимо рассчитать магнитный поток , через рамку в первом положении. Так как поле прямого бесконечного тока
 B1=
B1=![]() (1)
(1)
я
Рис. 2.13
интегральный метод. Разделим площадь рамки на столь узкие полосы, чтобы в пределах каждой такой полосы магнитное поле можно было бы приближённо считать однородным. Рассмотрим одну такую полоску шириной dx (рис 2.13), находящуюся на расстоянии x от прямого тока I1 . Элементарный магнитный поток через эту полоску
dФ=BdS=![]() (2)
(2)
Отсюда после интегрирования по x находим магнитный поток:
Ф=![]() (3)
(3)
Подставляя численные значения в (3)
Ф=![]() получаем
получаем
![]() Дж.
Дж.
Ответ: Дж.
Задача
2.15. В
однородном магнитном поле с индукцией
В=0,1 Тл равномерно вращается рамка,
содержащая N=1000
витков, с частотой n=10c![]() .
Площадь S
рамки равна 150 см
.
Площадь S
рамки равна 150 см![]() .
Определить мгновенное значение ЭДС
.
Определить мгновенное значение ЭДС
![]() ,
соответствующее углу поворота рамки
30˚.
,
соответствующее углу поворота рамки
30˚.
Дано В=0,1 Тл N=1000 N=10c S=150см
= α=30˚ |
ξi-? |
Мгновенное значение ЭДС ξi определяется основным уравнением электромагнитной индукции Фарадея-Максвела:
ξi =-dψ/dt (1)
Потокосцепление ψ=NФ, где N- число витков, пронизываемых магнитным потоком Ф. Подставив выражение ψ в формулу (1),
Получим:
ξi
=-N![]() (2)
(2)
При вращении рамки магнитный поток Ф, пронизывающий рамку в момент времени t, изменяется по закону Ф=BScosωt, где В- магнитная индукция; S-площадь рамки; ω-угловая частота. Подставив в формулу (2) выражение Ф и продифференцировав по времени, найдем мгновенное значение ЭДС индукции:
ξi =NBSωsinωt (3)
Угловая частота ω=2πn . Подставив выражение ω в формулу (3) и заменив ωt на угол α, получим:
ξi =2πnNBSsinα (4)
Произведя вычисления по формуле (4), найдем:
ξi
=![]()
Ответ: ξi =47,1 В
Задача 2.16. Катушку индуктивностью L=0,6 Гн подключают к источнику тока. Определите сопротивление катушки, если за время t=3с сила тока через катушку достигает 80% предельного значения.
Дано: L=0,6 Гн t=3c I=80%I0 |
R-? |
При замыкании цепи помимо внешней ЭДС ξ возникает ЭДС самоиндукции
![]() =
- L
=
- L![]() ,
препятствующая , согласно правилу Ленца,
возрастанию тока.
,
препятствующая , согласно правилу Ленца,
возрастанию тока.
В процессе включения источника тока нарастание силы тока в цепи задаётся функцией:
=![]() (1-e
(1-e![]() ),
),
где
τ![]() - время релаксации.
- время релаксации.
Следовательно, сила тока в любой момент определяется из выражения:
![]() (1-e
(1-e![]() )
(1)
)
(1)
Учитывая условия задачи, из выражения (1) находим:
0,8
=
(1-e![]() )
, 0,8=1-e
, e
= 0,2,
)
, 0,8=1-e
, e
= 0,2,
![]() , R=
-
, R=
-
![]() .
.
R=
-
![]() Ом
Ом
Ответ: R=321 мОм
Задача 2.17. В цепи шёл ток =50А. Источник тока можно отключить от цепи, не разрывая её. Определить силу тока в этой цепи через t=0,01с после отключения её от источника тока. Сопротивление R цепи равно 20 Ом, её индуктивность L=0,1 Гн.
Дано: Io=50A t=0,01c R=20Ом L=0,1Гн
|
I-? |
Вследствие явления самоиндукции при выключении Э.Д.С. ток в цепи спадает по
закону:
![]() (1)
(1)
Подставив в формулу (1) значение Io,R,L и t и вычислив, получим
I=50·e![]() =50·e
=50·e![]() =6,75
(А)
=6,75
(А)
Ответ: I=6,75 A
Задача
2.18. В
однородном магнитном поле (В=0,02Тл) вокруг
оси ,параллельной линиям индукции
,вращается тонкий однородный стержень
длины l=40
см . Ось вращения перпендикулярна стержню
и проходит через одну из его концов
(рис. 2.14). Угловая скорость ω=10с
![]() .
Найти разность потенциалов между осью
и серединой стержня, между серединой и
свободным концом стержня.
.
Найти разность потенциалов между осью
и серединой стержня, между серединой и
свободным концом стержня.
Дано: В=0,02 Тл l=40см=0,4м ω=10с |
(φо-φa)-? (φa-φc)-? |
П
д
Рис. 2.14
Лоренца:
![]() ,
(1)
,
(1)
являющейся в данном случае сторонней силой. Заряды разных знаков накапливаются на концах стержня, создают кулоновское поле, напряжённость которого
![]() (2)
(2)
Разность потенциалов между двумя любыми точками стержня
![]()
С учётом выражений (1) и (2) получим:
![]() =
-
=
-![]() (3)
(3)
Если
стержень вращается так, как показано
на рис 2.14, то электроны будут накапливаться
на закреплённом конце стержня и (![]() -
-
![]() ),
так же как и (
–
),
так же как и (
–
![]() ),
должна быть отрицательна
),
должна быть отрицательна
![]() ,
тогда
,
тогда
![]()
Так
как
![]() ,
то
,
то
![]() ;
; ![]()
Тогда
![]() =
= =
=
![]()
![]()

![]()
Ответ: - 4мВ; -12мВ.
Задача 2.19. Источник тока замкнули на катушку с сопротивлением R=10 Ом и индуктивностью L=1 Гн. Через сколько времени сила тока замыкания достигнет 0,9 предельного значения?
Дано: R=10 Ом L=1 Гн I=0,9Io |
t-? |
Ток в цепи, содержащей сопротивление R и индуктивностью L , вследствие явления самоиндукция при замыкании нарастает по закону:
![]() (1)
(1)
Подставляя в формулу (1) значения R,I,L и t, получим после преобразований:
0,9
![]() ;
0,9=1-e
;
0,9=1-e![]()
e =1-0,9=0,1 (2)
Логарифмируя выражение (2), найдём время t
Дано R1=5,0 Ом R2=95 Ом L=0,34 Гн
|
1) -? 2)
3)
|
Ответ: t =0,23 с
Задача
2.20. В
цепи , схема которого изображена на (рис
2.15)
![]() =50
Ом ,
=50
Ом ,
![]() =95
Ом, L=034
Гн, ξ =38 В. Внутреннее сопротивление
батареи пренебрежимо мало. Определить
силу тока в резисторе R2
в трех случаях: 1) до размыкания цепи;
2)в первый момент после размыкания;
3)через 0,01 с после размыкания.
=95
Ом, L=034
Гн, ξ =38 В. Внутреннее сопротивление
батареи пренебрежимо мало. Определить
силу тока в резисторе R2
в трех случаях: 1) до размыкания цепи;
2)в первый момент после размыкания;
3)через 0,01 с после размыкания.
Решение
1) Силу постоянного
тока до размыкания цепи находим по второму правилу Кирхгофа , применив его для контура abcda (рис 2.15)
![]() +
I·r=ξ
+
I·r=ξ

![]()
Рис
2.15
Рис.
2.15
где I- сила тока в батарее, r-внутреннее сопротивление источника.
Так как по условию r=0, то
=![]()
2)
Найдём силу тока
![]() в резисторе
сразу же после размыкания ключа. Если
в первом случае участки цепи bc,ef
были соединены между собой параллельно,
то после отключения батареи они, образуя
один неразветвлённый контур befcb
, оказываются соединёнными последовательно.
Участок ef
обладает индуктивностью, ток I1,
проходивший до размыкания цепи по этому
участку должен сохраняться, а ток
станет равным нулю. Следовательно,
в резисторе
сразу же после размыкания ключа. Если
в первом случае участки цепи bc,ef
были соединены между собой параллельно,
то после отключения батареи они, образуя
один неразветвлённый контур befcb
, оказываются соединёнными последовательно.
Участок ef
обладает индуктивностью, ток I1,
проходивший до размыкания цепи по этому
участку должен сохраняться, а ток
станет равным нулю. Следовательно,
![]() А.
А.
3)
Так как теперь цепь отключена от батареи,
ток начнёт убывать. Его величину
![]() в заданный момент t=0,01
с можно определить по формуле:
в заданный момент t=0,01
с можно определить по формуле:
![]()
для
изменения тока при замыкании и размыкании,
приняв в ней ξ=0 (случай размыкания),
![]() .
Тогда получим:
.
Тогда получим:
![]()
Подставив
числовые значения величин
![]() L,t
в формулу и вычислив, найдём
L,t
в формулу и вычислив, найдём
![]() =0,4
А
=0,4
А
Ответ:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]()
Задача
2.21. Две
катушки намотаны на один общий каркас.
Определить их взаимную индуктивность,
если при скорости изменения силы тока
в первой катушке
![]() во второй катушке индуцируется ЭДС
во второй катушке индуцируется ЭДС
Дано:
|
|
При
отсутствии ферромагнетиков коэффициенты
![]() одинаковы.
одинаковы.
Магнитный поток через вторую катушку
![]() .
.
По закону взаимной индукции ЭДС во второй катушке равна
![]() .
.
Откуда
 (Гн).
(Гн).
Ответ:
L![]() =0,1
Гн.
=0,1
Гн.
Задача 2.22. На стержень из немагнитного материала длиной =50см намотан в один слой провод так, что на каждый сантиметр длины стержня приходится 20 витков. Определить энергию W магнитного поля внутри соленоида, если сила тока в обмотке равна 0,5А. Площадь сечения стержня равна 2см .
Дано L=50см=0,5м N= I=0,5А S=2см |
W-?
|
Энергия магнитного поля соленоида с индуктивностью L , по обмотке которого течёт ток I , выражается формулой
W=![]() (1)
(1)
Индуктивность соленоида в случае немагнитного сердечника
зависит
только от числа витков на единицу длины
n
и от объема V
сердечника:![]() ,
где
,
где
![]() - магнитная постояннаяV=lS
–объем сердечника.
- магнитная постояннаяV=lS
–объем сердечника.
Подставив
в формулу (1) выражения
![]() ,
n,l,S,I
получим
,
n,l,S,I
получим
![]() .
(2)
.
(2)
![]() (Дж)=
(Дж)=
=62,8 мкДж.
Ответ: W=62,8 мкДж
Задача 2.23. Тороид с воздушным сердечником содержит 20 витков на 1 см. Определите объемную плотность энергии в тороиде , если по его обмотке протекает ток 3А.
Дано:
I=3А μ=1 |
w-? |
