
- •Методические указания
- •Предисловие
- •Электромагнетизм
- •1. Основные формулы
- •2. Примеры решения задач
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •3. Задачи для самостоятельного решения Поле прямого тока
- •Поле кривого тока
- •Закон полного тока. Магнитный поток. Магнитные цепи.
- •Работа по перемещению проводника с током в магнитном поле. Электромагнитная индукция. Индуктивность
- •Контрольные задания по электромагнетизму
- •Библиографический список
- •Содержание
- •Методические указания
- •394026 Воронеж, Московский просп., 14
Решение:
Магнитную индукцию в точке О найдем,
используя принцип суперпозиции магнитных
 полей
полей
![]() .
В нашем случае проводник можно разбить
на три части (рис. 2.4): два прямолинейных
проводника (1 и 3), одним концом уходящие
в бесконечность, и дугу полуокружности
(2) радиуса R.
.
В нашем случае проводник можно разбить
на три части (рис. 2.4): два прямолинейных
проводника (1 и 3), одним концом уходящие
в бесконечность, и дугу полуокружности
(2) радиуса R.
Тогда
![]() ,
где
,
где
![]() -
магнитные индукции поля в точке О,
создаваемые
током, текущим соответственно на первом,
втором и третьем участках проводника.
-
магнитные индукции поля в точке О,
создаваемые
током, текущим соответственно на первом,
втором и третьем участках проводника.
Так
как точка О лежит на оси проводника 1,
то
![]() и тогда
и тогда
![]() .
Учитывая, что векторы
.
Учитывая, что векторы
![]() и
и
![]() направлены в соответствии с правилом
буравчика перпендикулярно плоскости
чертежа от нас, геометрическое суммирование
можно заменить алгебраическим:
направлены в соответствии с правилом
буравчика перпендикулярно плоскости
чертежа от нас, геометрическое суммирование
можно заменить алгебраическим:
![]() .
.
Магнитную
индукцию поля
![]() можно найти, используя выражение для
магнитной индукции в центре кругового
можно найти, используя выражение для
магнитной индукции в центре кругового
проводника с током :
![]()
Так как магнитная индукция В2 создается в точке О половиной такого кругового проводника с током, то, учитывая равный вклад в магнитную индукцию от каждой половинки проводника, можно написать:
![]() .
(1)
.
(1)
Магнитную
индукцию
![]() найдем,
используя формулу (3) задачи 2:
найдем,
используя формулу (3) задачи 2:
В
нашем случае
![]() ,
,![]()
![]()
![]()
![]()
Тогда:
![]() .
.
Используя
найденные выражения
и
(1
и 2), получим:
![]() ,
,
или
![]()
Произведя вычисления, найдем В:
![]()
Ответ: В=331мкТл.
Задача 2.5. Определите магнитную индукцию на оси тонкого проволочного кольца радиусом R=5см, по которому течёт ток =10А, в точке А, расположенной на расстоянии d=10см от центра кольца.
Дано R=5см=0,05м I=10А |
В - ? |
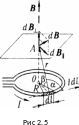 ешение:
ешение:
Магнитное кольцо создается током, текущий
по кольцу. Для решения задачи воспользуемся
законом Био-Савара – Лапласа:
![]() ,
(1)
,
(1)
где
—
магнитная индукция поля, создаваемого
элементом тока
![]() в
точке, определяемой радиус-вектором
.
в
точке, определяемой радиус-вектором
.
Выделим на кольце элемент и от него
в точку А проведем радиус-вектор (рис. 2.5).
Вектор направим в соответствии с правилом буравчика.
Запишем закон (1) в скалярном виде:
![]() (2)
(2)
где
![]() тогда
тогда
![]() (3)
(3)
Разложим
вектор
на составляющие
![]() и
и
![]() (рис2,5)
(рис2,5)
![]() ,
,
![]() ,
,
![]()
Согласно принципу суперпозиции магнитных полей, магнитная индукция в точке А определяется интегралом
![]() ,
,
![]()
где
интегрирование ведется по всем элементам
кольца. Так как
![]() параллельно плоскости кольца, то
параллельно плоскости кольца, то
![]() (из соображений симметрии), то
(из соображений симметрии), то
![]()
Подставим числовые значения в единицах СИ, вычислим:
![]()
Ответ: В=11,2 мкТл.
Задача
2.6. Замкнутый
тороид с железным сердечником имеет
N=400
витков из тонкого провода, намотанных
в один слой. Средний диаметр тороида
d=25cм.
Определить напряженность и индукцию
магнитного поля внутри тороида, магнитную
проницаемость
железа,
а также намагниченность
при значениях силы тока в обмотке тороида
![]() =0,5A
и
=0,5A
и
![]() =5A.
=5A.
Дано N=400 витков d=25см=0,25м
|
|
Применяя теорему о циркуляции вектора
вдоль окружности с диаметром d (средняя
линия тороида; рис 2.6)
![]() ,
,
находим напряженность магнитного поля
внутри тороида:
![]()
Отсюда после подстановки численных данных получаем:
![]() ,
,
![]() .
.
Далее, используя график на рис 1.2, определяем магнитные индукции:
![]() =0,9
Тл,
=1,45
Тл.
=0,9
Тл,
=1,45
Тл.
Затем
по формуле
![]() находим
магнитные проницаемости
находим
магнитные проницаемости
![]() :
:
![]() ,
,
![]() ,
,
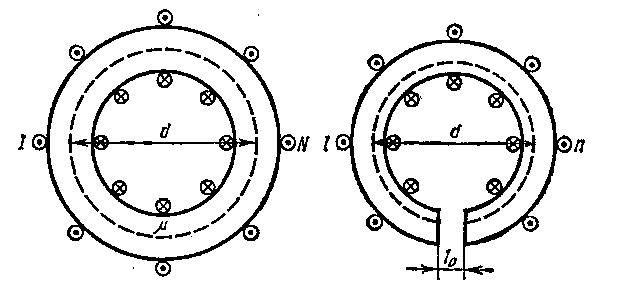
Рис. 2.6 Рис. 2.7
Анализ полученных данных позволяет установить, что силе тока пропорциональна только напряженность магнитного поля внутри ферромагнетика (железа), тогда как все остальные величины (индукция В, магнитная проницаемость , намагниченность ) являются нелинейными функциями H, а, следовательно, и нелинейными функциями силы тока .
Задача
2.7. Обмотка
тороида, имеющего стальной сердечник
с вакуумным зазором длиной
![]() =3мм,
содержит n=1000
витков на метр длины. Средний диаметр
тороида d=30см.
При какой силе тока
в обмотке тороида индукция
=3мм,
содержит n=1000
витков на метр длины. Средний диаметр
тороида d=30см.
При какой силе тока
в обмотке тороида индукция
![]() в зазоре равна 1Тл (рис 2.7).
в зазоре равна 1Тл (рис 2.7).
Дано: =3мм. n=1000 в/м d=30см =1Тл |
-? |
Применяя теорему о циркуляции вектора Н,
находим
![]() ,
(1)
,
(1)
где Н- напряженность магнитного
поля
в сердечнике,![]() -
напряженность
-
напряженность
магнитного поля в зазоре. Так как
относительная магнитная проницаемость
вакуума
![]() ,
то по формуле
,
то по формуле
![]() определяем напряженность магнитного
поля в зазоре:
определяем напряженность магнитного
поля в зазоре:
![]() ,
,
![]() .
.
Вследствие того, что вакуумный зазор узкий, будем считать радиальную составляющую вектора магнитной индукции и в зазоре, и в сердечнике равной нулю. Тогда, учитывая факт непрерывности нормальных (радиальных) составляющих вектора на границе раздела двух различных магнетиков:
![]()
Получим, что индукция в сердечнике по модулю равна .
По
графику (рис 1.2) определяем напряженность
магнитного поля в сердечнике:
![]()
![]() .
Таким образом, из (1) находим
.
Таким образом, из (1) находим
![]()
Ответ: =3,2A
Дано:
I=6A D<< d=1мм= |
k-? |
