
- •1. Производная. Правила дифференцирования
- •2. Таблица производных
- •3. Правила дифференцирования
- •4. Производные высших порядков
- •5. Дифференцирование функций, заданных неявно или параметрически
- •6. Уравнения касательной и нормали
- •7. Дифференциал первого порядка
- •8. Дифференциалы высших порядков. Формула Тейлора
- •9. Раскрытие неопределённостей по правилу Лопиталя
- •Задание 1
- •Задание 8
- •Задание 13
- •Задание 14
- •Задание 15
- •Задание 16
- •Задание 17
- •394026 Воронеж, Московский просп., 14
Задание 15
С помощью формулы Тейлора найдите приближённое значение числа с точностью до 0,001.
1) e2; 2) cos3/2; 3) ln4; 4) sin2;
5)
arctg2; 6)
![]() ;
7) sin3/2; 8) ln5; 9) cos2; 10)
arctg3; 11) e3/2;
12) cos1; 13) ln6; 14) sin3; 15) arctg3/2;
16) e5/2;
17) sin4; 18)
;
7) sin3/2; 8) ln5; 9) cos2; 10)
arctg3; 11) e3/2;
12) cos1; 13) ln6; 14) sin3; 15) arctg3/2;
16) e5/2;
17) sin4; 18)
![]() ;
19) cos3; 20) arctg 5/2;
;
19) cos3; 20) arctg 5/2;
21)
![]() ;
22) sin5/2; 23) cos4; 24) arctg 7/2;
;
22) sin5/2; 23) cos4; 24) arctg 7/2;
25)
e3;
26) sin 7/2; 27)
![]() ;
28) cos 9/2;
;
28) cos 9/2;
29) arctg 4; 30) sin5.
Задание 16
Найдите площадь треугольника, образованного прямой
x =x0+1, касательной и нормалью, проведёнными к графику заданной функции в точке с заданной абсциссой x0 или в точке, соответствующей значению параметра t0.
1)
![]() ;
2)
;
2)
![]() ;
;
3)
 4)
4)
![]() ;
;
5)
![]() ;
;
6)
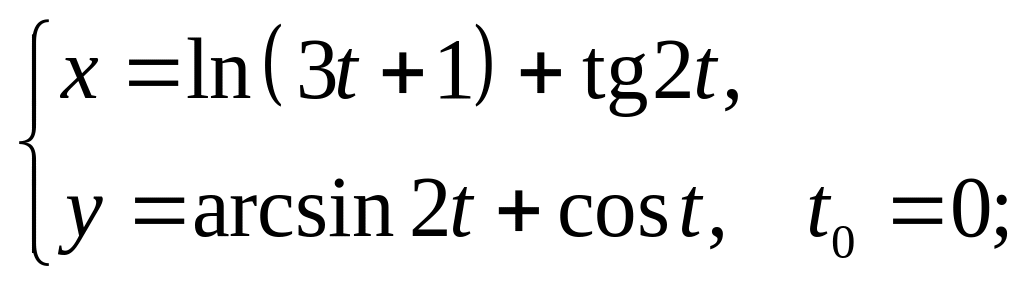
7)
![]() ; 8)
; 8)
![]() ;
;
9)
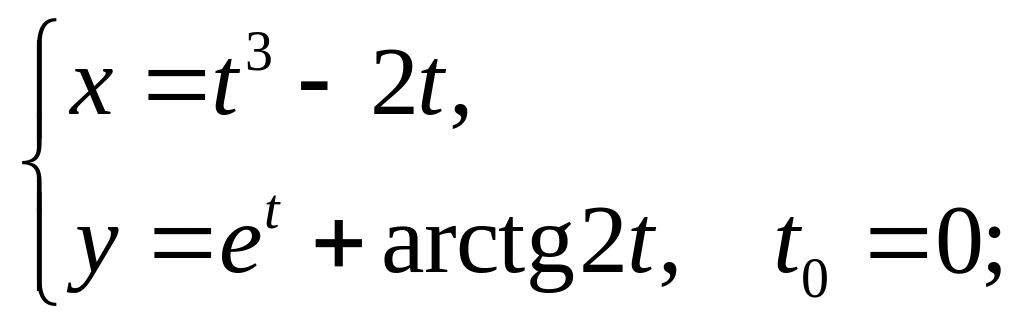 10)
10)
![]() ;
;
11)
![]() ;
;
12)
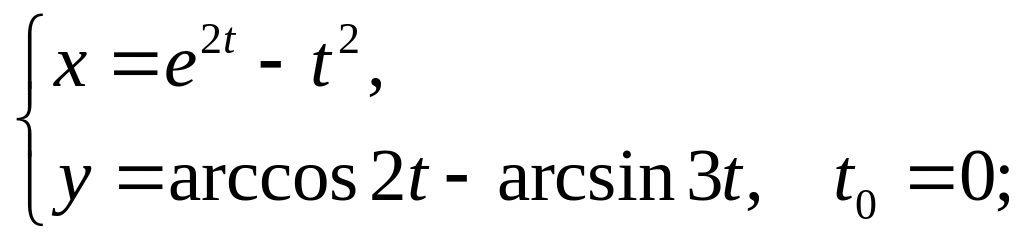
13)
![]() ;
14)
;
14)
![]() ;
;
15)
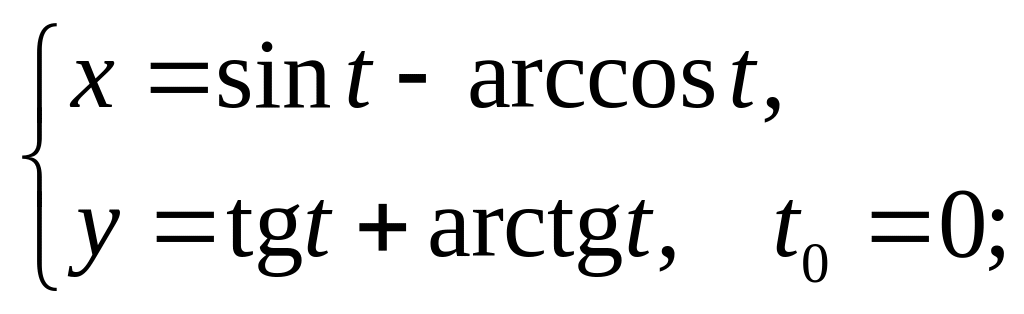 16)
16)
![]() ;
;
17)
![]() ;
;
18)
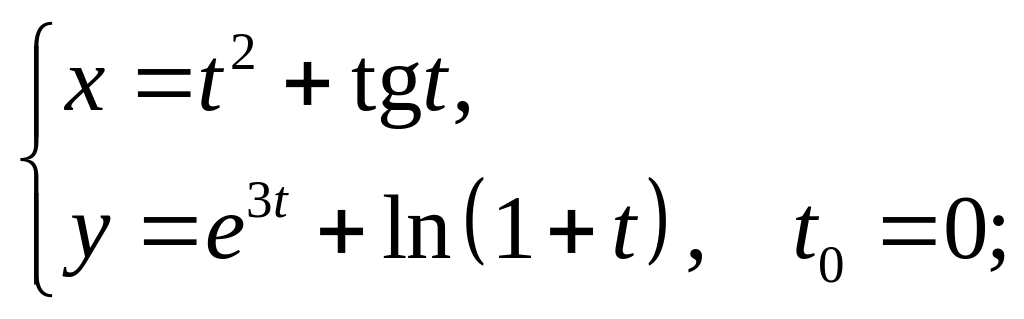
19)
![]() ; 20)
; 20)
![]() ;
;
21)
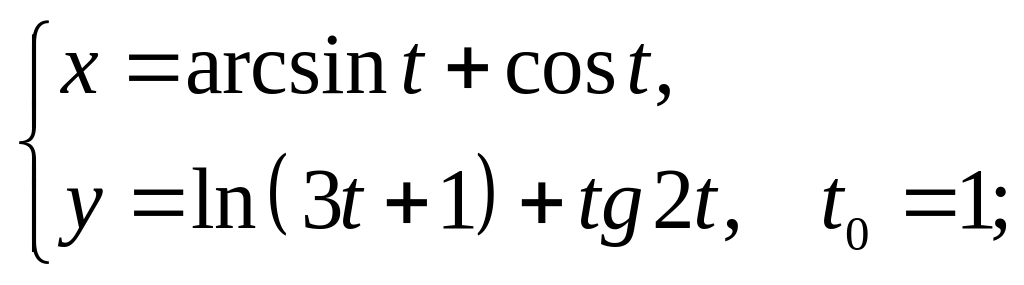 22)
22)
![]() ;
;
23)
![]() ; 24)
; 24)
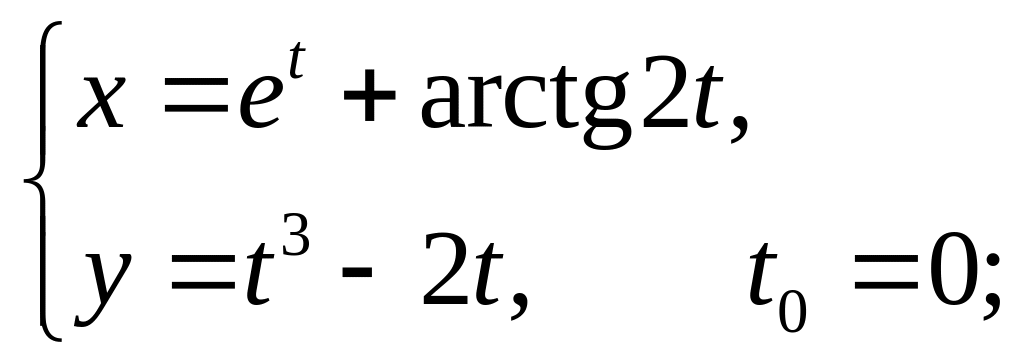
25)
![]() ;
26)
;
26)
![]() ;
;
27)
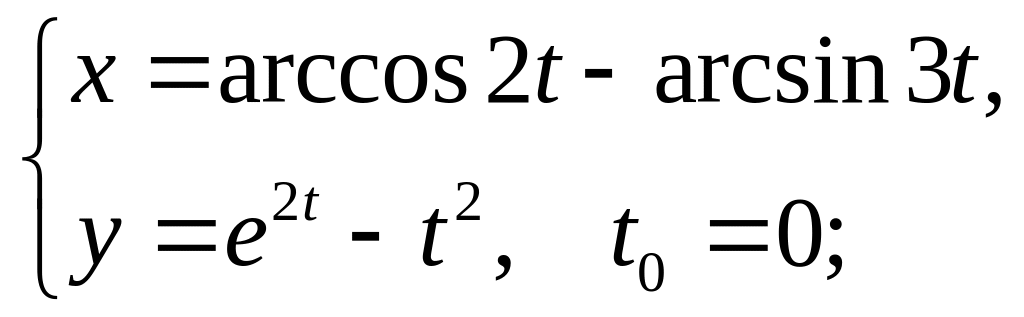 28)
28)
![]() ;
;
29)
![]() ;
30)
;
30)
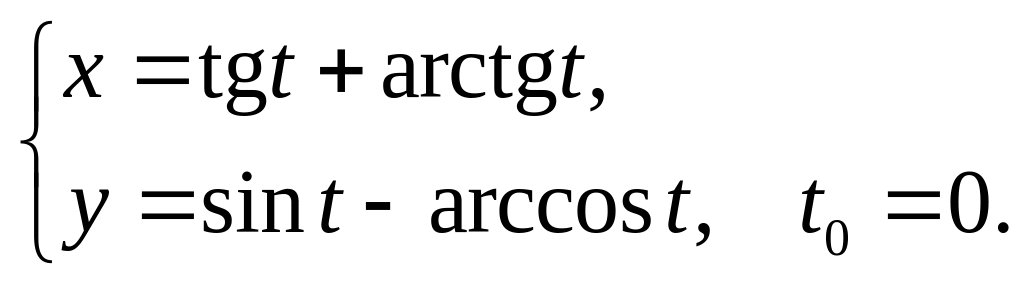
Задание 17
Пользуясь правилом Лопиталя, найдите пределы.
1.
a)
![]() ;
б)
;
б)
![]() ;
;
2.
a)
![]() ; б)
; б)
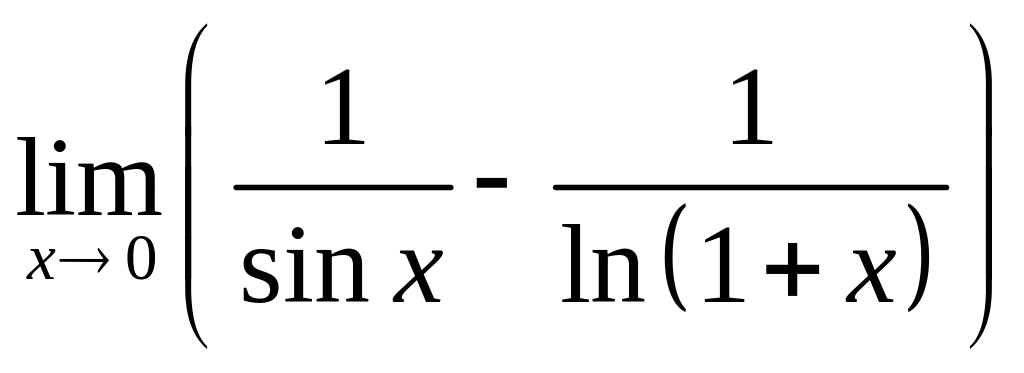 ;
;
3.
a)
![]() ; б)
; б)
![]() ;
;
4.
a)
![]() ; б)
; б)
![]() ;
;
5.
a)
![]() ; б)
; б)
![]() ;
;
6.
a)
![]() ;
б)
;
б)
![]() ;
;
7.
a)
![]() ;
б)
;
б)
![]() ;
;
8.
a)
![]() ;
б)
;
б)
![]() ;
;
9.
a)
![]() ;
б)
;
б)
![]() ;
;
10.
a)
![]() ;
б)
;
б)
![]() ;
;
11.
a)
![]() ;
б)
;
б)
![]() ;
;
12.
a)
 ;
б)
;
б)
![]() ;
;
13.
a)
![]() ;
б)
;
б)
![]() ;
;
14.
a)
![]() ;
б)
;
б)
![]() ;
;
15.
a)
![]() ;
б)
;
б)
![]() ;
;
16.
a)
![]() ;
б)
;
б)
![]() ;
;
17.
a)
 ; б)
; б)
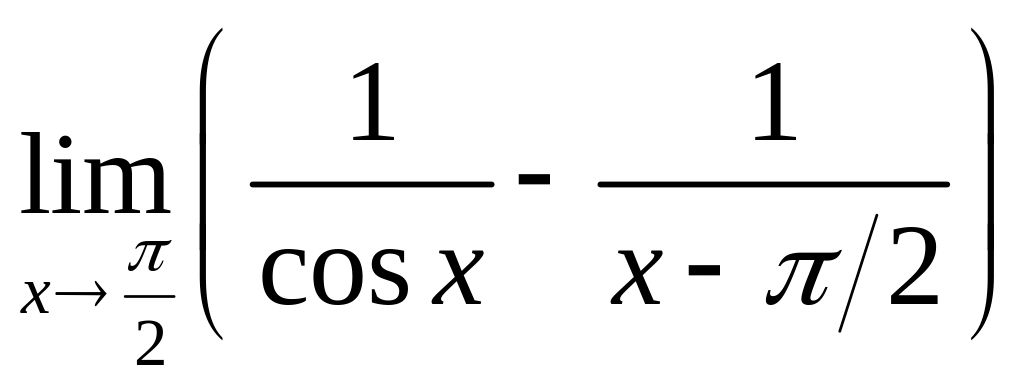 ;
;
18.
a)
![]() ; б)
; б)
![]() ;
;
19.
a)
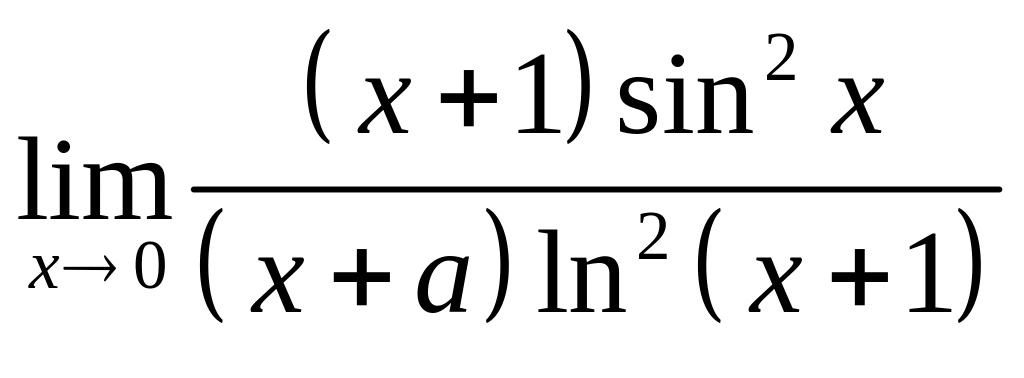 ; б)
; б)
![]() ;
;
20.
a)
![]() ; б)
; б)
![]() ;
;
21.
a)
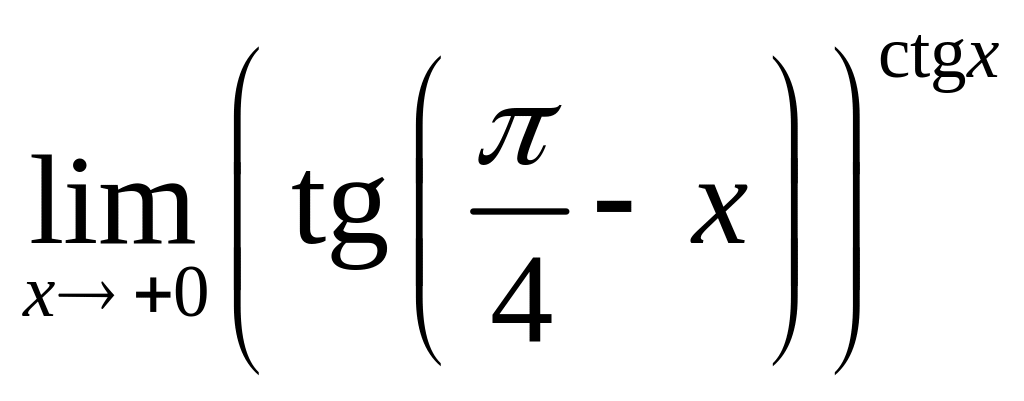 ; б)
; б)
![]() ;
;
22.
a)
![]() ; б)
; б)
![]() ;
;
23.
a)
![]() ; б)
; б)
![]() ;
;
24.
a)
![]() ; б)
; б)
![]() ;
;
25.
a)
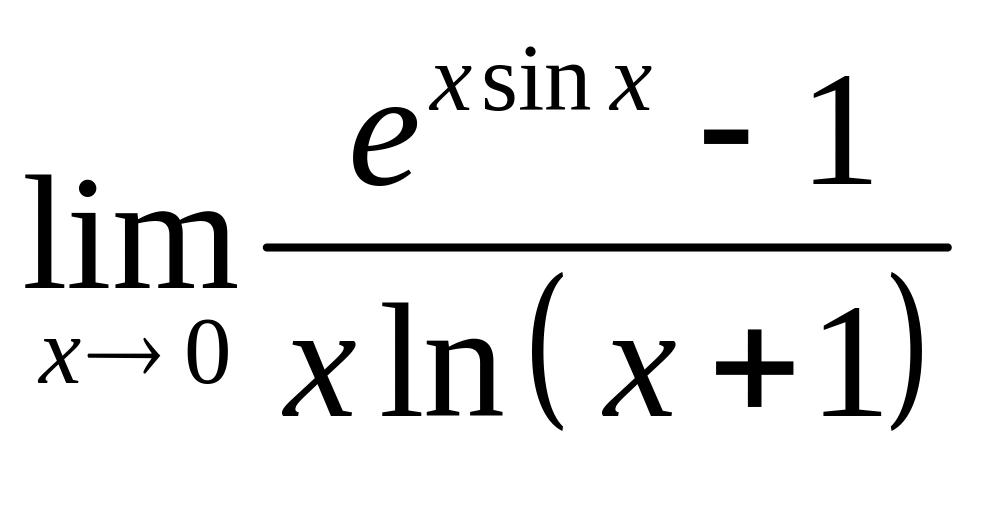 ; б)
; б)
![]() ;
;
26.
a)
![]() ; б)
; б)
![]() ;
;
27.
a)
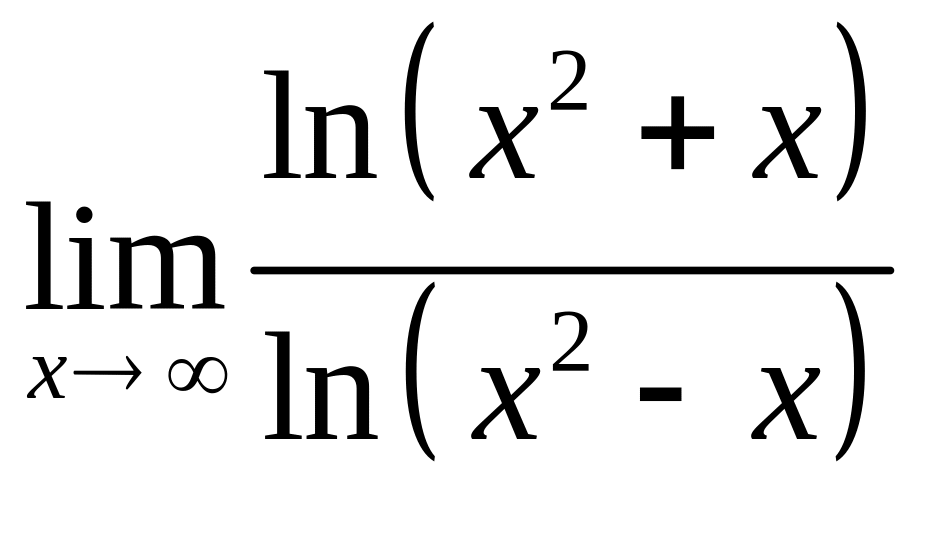 ; б)
; б)
![]() ;
;
28.
a)
![]() ; б)
; б)
![]() ;
;
29.
a)
![]() ; б)
; б)
![]() ;
;
30.
a)
![]() ;
б)
;
б)
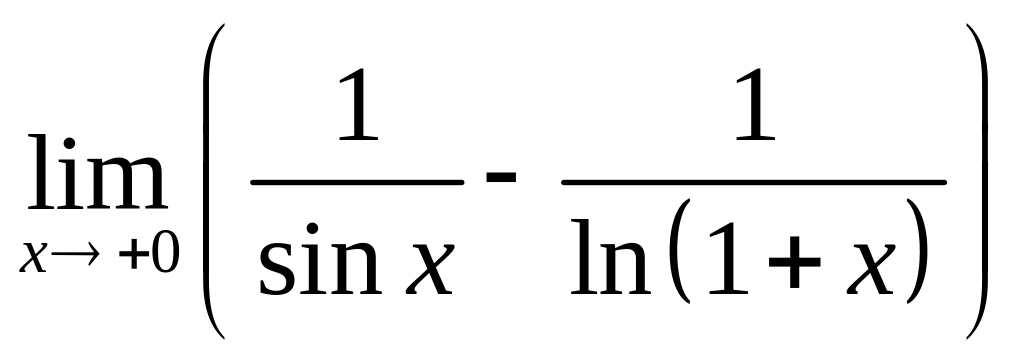 .
.
Библиографический список
1. Пискунов Н.С. Дифференциальное и интегральное исчисления/ Н.С. Пискунов.- М.: Наука, 2001. Т.1.- 250 с.
2. Зимина О.В. Высшая математика/ О.В. Зимина, А.И. Кириллов, Т.А. Сальникова.- М.: Физматлит, 2005.-368 с.
3. Сборник задач по математике для втузов. Ч.1: Линейная алгебра и основы математического анализа/ В.А. Болгов, Б.П. Демидович, А.В. Ефимов и др.- М.: Наука,1993.- 480 с.
4. Красс М.С. Математика для экономистов: Учеб. пособие/ Красс М.С. , Чупрынов Б.П.- СПб.: Питер, 2009.-464с.
5. Кремер Н.Ш. Высшая математика для экономических специальностей: учебник и практикум/Н. Ш. Кремер, Б.П. Путко, И.М. Тришин, М.Н. Фридман; под ред. Н.Ш. Кремера.-М.: Изд. Юрайт; Высшее образование, 2010.-909 с.
6. Кузнецов Л.А. Сборник заданий по высшей математике. Типовые расчеты: Учебное пособие. - СПб. : Издательство «Лань», 2005.-240 с.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
для организации самостоятельной работы
по изучению раздела «Производная»
курса «Математический анализ»
для студентов направления подготовки бакалавров 080100 «Экономика»
очной формы обучения
Составители:
Глушко Елена Георгиевна
Максимова Екатерина Игоревна
В авторской редакции
Компьютерный набор Е.Г. Глушко
Подписано к изданию 28.02.2014
Уч.- изд. л. 2,5.
ФГБОУ ВПО «Воронежский государственный
технический университет»
